2019-11-03 21:37:59
一、Diameter of Binary Tree
问题描述:

问题求解:
解法一、第一反应是树上动归,每个节点保存一下左右的最大深度,最后以每个节点作为中枢计算最大的长度即可。
public int diameterOfBinaryTree(TreeNode root) {
Map<TreeNode, int[]> map = new HashMap<>();
dfs(root, map);
int res = 0;
for (TreeNode key : map.keySet()) {
res = Math.max(res, map.get(key)[0] + map.get(key)[1]);
}
return res;
}
private int[] dfs(TreeNode root, Map<TreeNode, int[]> map) {
if (root == null) return new int[]{-1, -1};
int[] l = dfs(root.left, map);
int[] r = dfs(root.right, map);
map.put(root, new int[]{Math.max(l[0], l[1]) + 1, Math.max(r[0], r[1]) + 1});
return map.get(root);
}
解法二、不求直径,而是转求每个节点的最大深度,遍历的时候可以顺便得到直径。
public int diameterOfBinaryTree(TreeNode root) {
int[] res = new int[1];
helper(root, res);
return res[0];
}
private int helper(TreeNode root, int[] res) {
if (root == null) return 0;
int l = helper(root.left, res);
int r = helper(root.right, res);
res[0] = Math.max(res[0], l + r);
return Math.max(l, r) + 1;
}
二、Tree Diameter
问题描述:
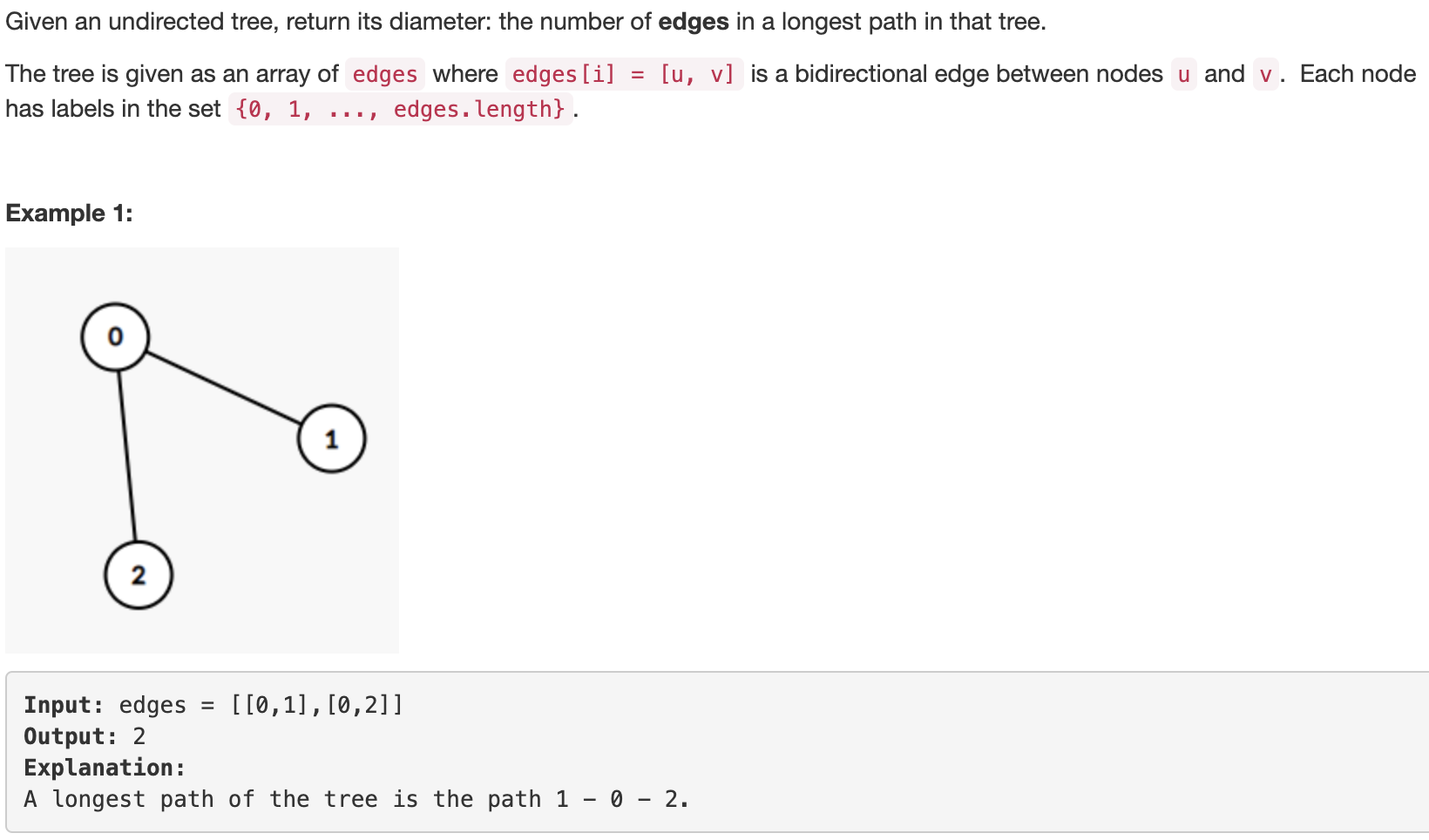
问题求解:
int res = 0;
public int treeDiameter(int[][] edges) {
Map<Integer, Set<Integer>> graph = new HashMap<>();
for (int[] edge : edges) {
int u = edge[0];
int v = edge[1];
if (!graph.containsKey(u)) graph.put(u, new HashSet<>());
if (!graph.containsKey(v)) graph.put(v, new HashSet<>());
graph.get(u).add(v);
graph.get(v).add(u);
}
helper(graph, 0, new HashSet<Integer>());
return res;
}
private int helper(Map<Integer, Set<Integer>> graph, int node, Set<Integer> used) {
Integer first = null;
Integer second = null;
used.add(node);
for (int next : graph.get(node)) {
if (used.contains(next)) continue;
int tmp = helper(graph, next, used);
if (first == null || first < tmp) {
second = first;
first = tmp;
} else if (second == null || second < tmp) second = tmp;
}
int l1 = first == null ? 0 : first + 1;
int l2 = second == null ? 0 : second + 1;
res = Math.max(res, l1 + l2);
return l1;
}