(FFT)学习笔记
因为已经有比我写的好的了,所以这里就不会重头讲,只讲一些自己需要用的而已。
(FFT)解决什么呢?解决两个多项式快速相乘的问题。
我们设第一个多项式为(F(x)),第二个多项式为(G(x)).
多项式(F(x))的项数为(n) ,多项式(G(x))的项数为(m).
乘出来的多项式为(W(x)).项数为((n+m-1)).
入门基本:初中一年级学历
DFT
过程:把系数表达转换为点值表达
相信大家都学过了待定系数法啦
把一个多项式转换为点值表达应该不难
显而易见,把一个(n)次多项式转换为点值表达,需要(n+1)个坐标。
我们把这些(F(x))坐标记为:((x_0,y_0);(x_1,y_1);(x_2,y_2)……)
我们把这些(G(x))坐标记为:((x_0,y^*_0);(x_1,y^*_1);(x_2,y^*_2)……)
那么(W(x))坐标就为:((x_0,y_0*y^*_0);(x_1,y_1*y^*_1);(x_2,y_2*y^*_2)……)
那么我们的问题就在于如何将(F)和(G)转换为点值表达。
求出(F)和(G)的点值表达,就可以快速算出(W)的点值表达了。
复数
在学习DFT之前,还要先学学这个——复数
虚数
定义:(i^2=-1)
实数和虚数的组合就是复数,记为(a+bi)
PS:(i^2)要化简为(-1)
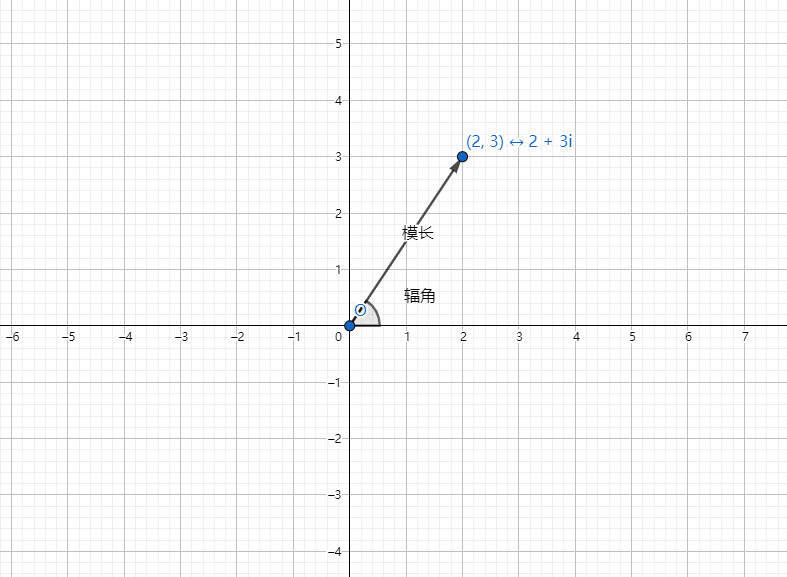
复数的 模长 指它的长度(到原点的距离),辐角 指它与原点的连线,与 (x) 轴(逆时针)的夹角。如图,复数(2+3i) 的模长和辐角都已标出(引用longlongzhu123的博客)
代码定义复数
结构体存储:一个存实数部,一个存虚数部
struct Complex{
double r,i;
Complex():r(0),i(0){} //初始化
Complex(double R,double I) : r(R),i(I){} //同r=R,i=I,给一个虚数赋值
Complex(const Complex& c) : r(c.r),i(c.i){} //等同r=c.r,i=c.i
};
复数运算
我们设两个复数(x,y), (x=a_0+b_0i),(y=a_1+b_1i) . 一个实数(k) .
加法
减法
乘法
运算的几何意义(非重要)
(引用longlongzhu123的博客)
加法
例子:((2+3i)+(3+1i)=5+4i)
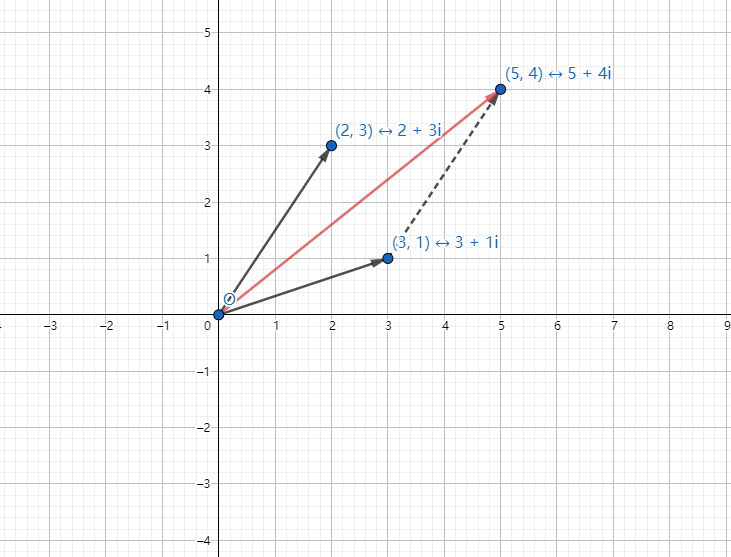
意义:发现什么了吗?没有?看看那条虚线跟$ 2+3i$ 有什么关系?没错。虚线与 (2+3i)平行。(2+3i) 和 (3+1i)相加的结果可以看成在 (3+1i) 的端点处向上数$3 $格,向右数 (2) 格得到的点。或者说是两个复数所组成平行四边形的一条对角线。(理解一下这句话)
乘法
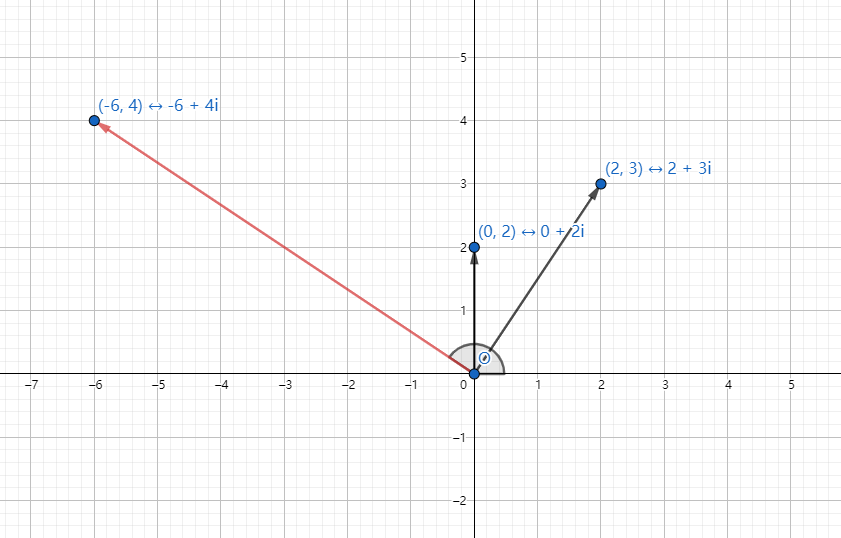
复数乘法也有几何意义。一句话:模长相乘,辐角相加。
代码实现运算
重载看不到不要紧,直接看(return)就ok了。(记住返回的也是复数,用结构体存)
inline Complex operator+(const Complex&a,const Complex&b){return Complex(a.r+b.r,a.i+b.i);} //复数+
inline Complex operator-(const Complex&a,const Complex&b){return Complex(a.r-b.r,a.i-b.i);} //复数-
inline Complex operator*(const Complex&a,const Complex&b){ //复数*
return Complex(a.r*b.r - a.i*b.i , a.r*b.i + b.r*a.i );
}
单位根
单位圆:在复平面上一个模长为(1)的圆 ,长下面这个样子。
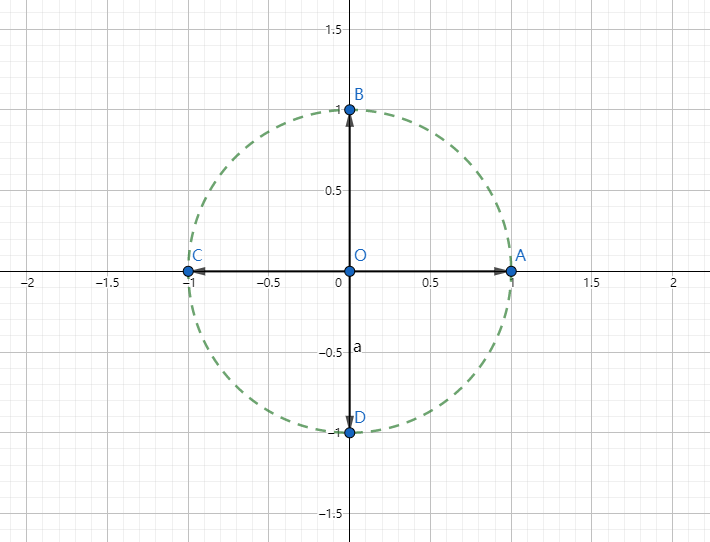
n次单位根:把单位圆平分成(n)份,取其中第一份(从x轴的正半轴开始逆时针平分)
例子:(3)次单位根,长下面那样,(B)点即为(3)次单位根。
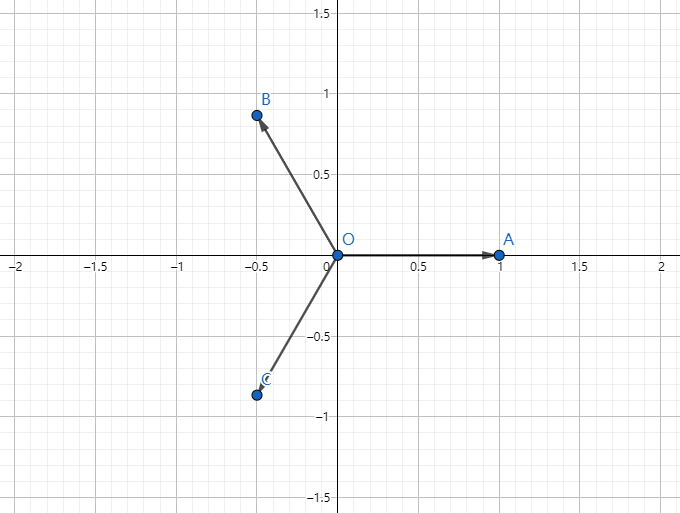
我们把n次单位根记为:(omega_n)或(omega_n^1)
那剩下的(n-1)个点(指上面的(A)和(C)点)怎么表示呢?
我们发现,(B)点是从(x)轴正半轴开始逆时针数的第一个点((A)点是第(0)个,记作(omega^0_n)),所以它记作(omega^1_n),那么(C)点是第二个点,它记作(omega^2_n)。同理,第(k)个点就叫(omega^k_n),另外(omega^k_n=(omega_n)^k)。
单位根的性质
(引用至command_block的blog)
单位根的世界,就是一个单位圆。
-1. $ forall x:omega_n^0=1(,(翻译成人话:对于任意的n,)omega_n^0=1$)
0.(omega^k_n=(omega_n)^k)
1.(omega_n^j*omega_n^k=omega_n^{j+k})
2.(omega_{2n}^{2k}=omega_n^k)
3.当(n)为偶数时,(omega_n^{(k+n/2)}=-omega_n^k)
4.(sum_{i=1}^{n} omega_n^i=0)
5.(omega_n^1=(cos(frac{2pi}{n}),sin(frac{2pi}{n}))) (注:左边为实数部,右边为虚数部)
6.(omega_n^k=omega_n^{k\%n})