其实这里只不过是个人学数据结构的总结罢了
咕了,以后再更新。。。
前言
OI中的算法有很多,不同算法解决的问题不一样,时间复杂度也不一样,那么在众多OIer中,就有一些毒瘤,他们弄出了可以让程序变快的东西。那就是数据结构。另外,数据结构都很毒瘤,他们都有一个特点,就是代码特长。
基础数据结构入门
其实并不是所有数据结构都很难,下面就讲一下最基础的数据结构,他们是“队列”,“优先队列”,“栈”,“动态数组”。
队列
队列是个什么呢?队列是一种先进先出的数列。
简单的说,队列就像是食堂排队等饭,先来的先吃饭(不考虑插队情况)。然后排队当然有几种操作。
1.看看队首那个人是谁,好扣他钱
2.队首那个人打好了饭,赶走他
3.又来新的人排队
这就是队列的基本操作,他们分别对应的代码是
q.front();
q.pop();
q.push(新来的人);
这些只是STL的操作,那STL是什么呢
STL
STL是C++的一个库,他封装了C++很多的算法,使用起来非常方便,但相对于自己用数组实现起来会慢一些。但STL是针对于O2优化而开发的,所以在开O2情况下,STL会跑得很快,以至于比手写的还要快。本文章并不专讲STL,如果想全面了解STL可以到度娘那搜一下。
想要调用STL的队列就要包括头文件:
#include<queue>
定义一个队列是这样的:
queue<队列类型:int,char之类的>变量名;
优先队列
优先队列是在队列的基础之上,多了个优先级,也就是说,你本来排队快可以领饭盒了,这时候突然来了一个人,按理来说他肯定要排你后面,但是他竟然是有病条的人,那么他就可以排你前面,毕竟要尊重得病之人。如果此时来了个病更加重的人,那么他就排你俩前面了。
那么优先队列就是这样的,病越重,优先级越高,就越靠近队首。
和队列一样也是那三种操作:
q.top();//和队列的q.front()意思一样
q.pop();
q.push(新来的人);
和队列所包含的头文件一样,定义有点不一样:
priority_queue<队列类型:int,char之类的>变量名;
栈
与队列相反,栈是一种先进后出的数据结构。就是说先来的会比后来的更晚出去。
简单的说,你走入一个栈内,如果没有意外的话,一接到出栈命令就可以出栈了。但是,如果来了其他人,那么就要等到其他人都出完栈了,你才可以出栈。
栈有三种基本操作:
1.查看栈顶是谁(和队列的1操作一样)
2.弹出栈顶元素(和队列的2操作一样)
3.将新元素压入栈内(和队列的3操作一样)
分别对应的代码:
q.top();
q.pop();
q.push();
这里使用的依然是STL。需包含头文件
#include<stack>
定义
stack<队列类型:int,char之类的>变量名;
动态数组
从名字可以看出,这个东西的本质是数组,所以动态数组可以像数组一样随机访问。
至于动态数组有什么优点,那就是省空间。有时候为了题目的限制,我们会将数组开得很大,然而实际上有很多空间是不需要用的,如我定义了一个100的数组,然而真正需要用的只有10这么多,那就浪费了90的空间。而动态数组的优点就在这里了,他不会有这种浪费,也就是动态数组的空间是会发生改变的!
这里介绍几个动态数组的基本操作:
1.push_back 将一个元素加入到动态数组
v.push_back(要插入的元素);
2.size() 查询动态数组此时的空间大小
s=v.size();
3.clear() 清空动态数组
v.clear();
这里还是用STL,需包含头文件
#include<vector>
定义:
vector<队列类型:int,char之类的>变量名;
结束言
恭喜!你已经学会了最基础的数据结构了,打好基础,相信将来的复杂数据结构你一定都可以学会。
数据结构进阶:线段树
学会了基础的数据结构,那么就可以学一些比较毒瘤的数据结构了,在这些数据结构中,思想最简单,也是最容易实现的,就是线段树!
线段树解决是区间问题,例如:【模板】树状数组 1 ,【模板】树状数组 2 ,【模板】线段树 1
首先看看线段树的结构,他是一颗树,据有树的性质。如下图:这就是一颗线段树。
(color{red} ext{红色}) :节点编号 ; (color{blue} ext{蓝色}):感性理解(看图就懂了吧,父子关系);(color{green} ext{绿色}):每个点的权值。
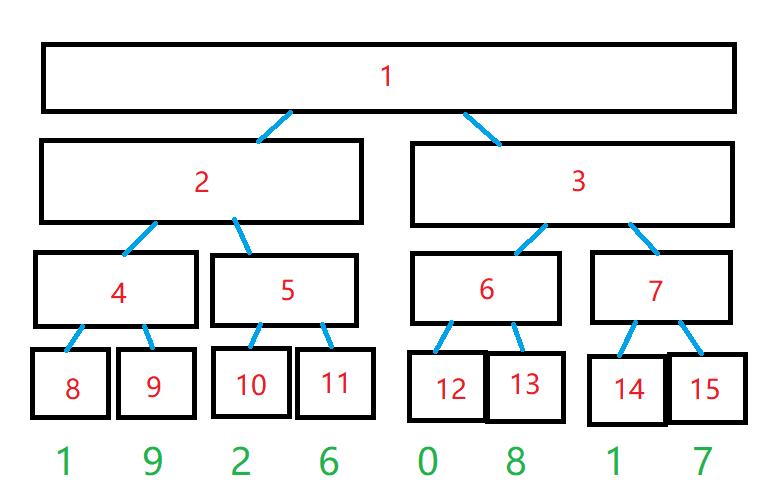
我们来看看(color{red} ext{红色})有什么奇妙的性质吧。
有人就会说:依节点深度,从左至右依次增加.
对了吗?对!但能不能更具体一点?这样计算机听不懂啊!
性质1:对于一个节点编号为(x),它的左儿子编号为((x*2)),右儿子编号为((x*2+1))。
转换为代码:
#define L(node) (node*2)
#define R(node) (node*2+1)
或许有人看不懂#define 是什么意思,第一句语句的意思是:代码中凡是遇到L(node)这个语句,都将其解释为(node*2),所以L(node)就相当于表示node的左儿子。第二句同理。如果还是没看懂,没关系,我下面会结合代码解释。
那建出这些节点有什么用呢?
线段树维护信息
细心的人会发现,上面的图,(1)号节点画得特别大,扩住了整个序列。编号越大,节点越小(指形状)。
那么这些节点的大小(指形状)代表什么呢? 代表区间的大小!
例如:(1)号节点代表的区间是({1,2,3,4,5,6,7,8}) ,(5)号节点代表的区间是({3,4}),(13)号节点代表的是({6})
明显:最底下的(8)个叶子节点就代表整个序列的一个位置。
那么我们就可以将权值赋值到叶子节点上了。
例如:(8)号节点的权值为(1),(11)号节点的权值为(6),(15)号节点的权值为(7)。
假如我们要维护的是区间和。
那么区间([1,2])的值就是(区间([1])的值+区间([2])的值)。
代表区间([1,2])的节点是(4)号节点。代表区间([1])的节点是(8)号节点。代表区间([2])的节点是(9)号节点。
(8)和(9)号节点的权值我们都知道。
那么(4)号节点的权值不就可以求出来了吗。
并且我们惊奇的发现(8)和(9)号节点就是(4)号节点两个儿子。
性质2:对于一个节点(x),(x)的信息从(x)的两个儿子转移得到
这个转移我们可以写成函数pushup(这是主流写法),例如要维护区间和:((tree)数组代表权值)
void pushup(int node){
tree[node]=tree[L(node)]+tree[R(node)];
}
由此可以看出线段树是自底向上的数据结构。
线段树的实现(一)
线段树的实现是通过递归实现的。
建树
我们只需要将叶子节点的信息都赋值好,剩下的可以不断pushup上去。
递归时传(3)个参数:(node)当前节点编号,(begin)当前区间左边界,(end)当前区间右边界。
那么我们从(1)号节点(根节点),向下递归,递归左儿子,递归右儿子。
直到到叶子节点为止。((begin==end))
叶子节点信息为序列当前位置的值。((tree[node]=a[begin]),(a)数组为输入的初始值)
递归完左、右儿子,pushup一遍,返回。
到现在为止,我只不过是讲了些线段树的性质罢了。下面我们来讲线段树的操作。
操作
线段树最普遍的操作就是区间修改,区间查询.(当然还有什么优化建边什么的,我之后再讲。)
查询
假如我们要查询一个位置(x)的值,怎么做?
这不直接输出(a[x])就可以了吗?(???
是的(汗)。那用线段树怎么做?
嗯……(认真思考),递归到(x)所对应的叶子节点(node),输出权值。(灵机一动)
没错,看来基础还挺扎实的吗。
单点查找的线段树十分简单,只需要递归到相应的叶子节点,返回叶子节点信息即可。
查询一:找到要修改位置对应的叶子节点位置,返回节点值
假如我们要查询一个区间([x,y])的值,怎么做?
前缀和!(得意
是的(汗)。那用线段树怎么做?
嗯……(认真思考),将区间所有点都像上面一样查一遍,相加。(虚
ε=( o`ω′)ノ怒!线段树的节点意义忘了吗!
哦……(咕
例如我们要查询区间([2,6])的和。
可以发现([2,6])区间是可以由几个区间组合而成的:([2]),([3,4]),([5,6]).
如上图(很上的图),这三个区间都分别对应着线段树中的三个节点。
那我们将那三个节点的值相加即可得到答案。(高明)
修改
假如我们要修改序列中一个位置(x)的值,怎么改?
直接改掉!(暴力,傲娇
那你爸怎么办?
呃呃呃额,
pushup上去吧(虚了一点
太棒了!就这样。
Σ(っ °Д °;)っ惊!(。。。
单点修改的线段树就如上面对话的方式那样:
修改一:找到要修改位置对应的叶子节点位置,直接改掉,然后pushup上去。
假如我们要修改序列中一段区间([x,y])的值,怎么改?
直接改掉!(暴力,傲娇
怎么直接改?
呃呃呃额,一个一个点修吧(虚了
真是笨啊,线段树的节点意义忘了吗!
难道……(咕
#include<bits/stdc++.h>
#define maxn 40000000
#define int long long
using namespace std;
int tree[maxn],tag[maxn],a[maxn];
int n,m,x,y,z,mode,t;
void maketree(int node,int begin,int end){
if(begin==end){
tree[node]=a[begin];
return ;
}int mid=(begin+end)/2;
maketree(node*2,begin,mid);
maketree(node*2+1,mid+1,end);
tree[node]=tree[node*2]+tree[node*2+1];
}
void pushdown(int node,int begin,int end){
if(tag[node]){
tag[node*2]+=tag[node];
tag[node*2+1]+=tag[node];
int mid=(begin+end)/2;
tree[node*2]+=tag[node]*(mid-begin+1);
tree[node*2+1]+=tag[node]*(end-mid);
tag[node]=0;
}
}
void update(int node,int begin,int end,int x,int y,int val){
if(begin>=x&&end<=y){
tree[node]+=val*(end-begin+1);
tag[node]+=val;
return ;
}int mid=(begin+end)/2;
pushdown(node,begin,end);
if(x<=mid)update(node*2,begin,mid,x,y,val);
if(y>mid)update(node*2+1,mid+1,end,x,y,val);
tree[node]=tree[node*2]+tree[node*2+1];
}
int query(int node,int begin,int end,int x,int y){
if(begin>=x&&end<=y){
return tree[node];
}int mid=(begin+end)/2,res=0;
pushdown(node,begin,end);
if(x<=mid)res+=query(node*2,begin,mid,x,y);
if(y>mid)res+=query(node*2+1,mid+1,end,x,y);
return res;
}
signed main(){
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
}
maketree(1,1,n);
for(int i=1;i<=m;i++){
scanf("%lld",&mode);
if(mode==1){
scanf("%lld%lld%lld",&x,&y,&z);
update(1,1,n,x,y,z);
}if(mode==2){
scanf("%lld%lld",&x,&y);
printf("%lld
",query(1,1,n,x,y));
}
}
return 0;
}