扩欧讲解

$ $扩欧讲解

前记

$ $本蒟蒻的第二篇blog，之前学了扩欧却一直没时间写，现在趁着“山竹”台风，学校放假，写一下扩欧（qwq都忘得差不多了）

前提摘要

$ $ what is 扩欧？

$ $扩欧及是扩展欧几里得，是欧几里得算法的扩展算法。

$ $欧几里得算法是蛤？就是小学学过的辗转相除法。用于计算两个整数a,b的最大公约数。代码：

int gcd(int a,int b){
    return b?gcd(b,a%b):a;
}

扩欧的基本问题：求解ax+by=c的所以整数解（a,b,c都为整数）

首先：要保证有整数解就必须有：gcd(a,b)|c.

证明：
gcd(a,b)|ax,gcd(a,b)|by (Rightarrow) gcd(a,b)|ax+by (Rightarrow) gcd(a,b)|c

然后，我们思考求ax+by=c的一组特解

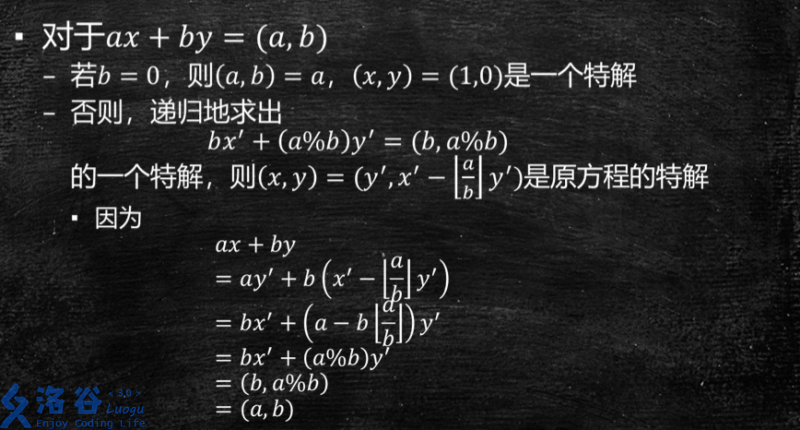
代码：

int exgcd(int a, int b, int &x, int &y)
{
	if (b == 0)
    {
        x = 1;
        y = 0;
        return a;
    }
    int q = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return q;
}

线性同余方程

ax (equiv) b (mod n)

换句话说：ax mod n = b mod n

性质： 满足同加性，同减性，同乘性，同幂性，但不满足同除性

那么 b mod n = b - nq (q为b除以n)

$ $ ax mod n = ax - np (p为ax除以n)

$ $ y=q-p

则 ax (equiv) b (mod n)$ (等价于) $ ax+ny=b

这样就转化成了扩欧啦。QAQ

洛谷【P1082同余方程】代码：

#include<cstdio> 
using namespace std;
long long a,b,x,y,k;
void gcd(int a,int b)
{
    if(b==0)
    {
        x=1;y=0;
        return;
    }
    gcd(b,a%b);
    k=x;x=y;y=k-a/b*y;
}
int main()
{
    scanf("%d%d",&a,&b);
    gcd(a,b);
    printf("%d",(x+b)%b);
    return 0;
}

求逆元

可用费马小定理和欧拉定理解决

扩欧方法：

可转化为 ax (equiv) 1 (mod n)，gcd(a,n)=1;

是不是看上去和同余方程很像。没错了，就是同余方程。

洛谷【P3811乘法逆元】代码：

#include<cstdio> 
using namespace std;
long long a,b,x,y,k;
void gcd(int a,int b)
{
    if(b==0)
    {
        x=1;y=0;
        return;
    }
    gcd(b,a%b);
    k=x;x=y;y=k-a/b*y;
}
int main()
{
    scanf("%d%d",&a,&b);
    gcd(a,b);
    for(int i=1;i<=a;i++){
    	gcd(i,b);
   		printf("%d
",(x+b)%b);
   	}
    return 0;
}

后记

实话：本蒟蒻实在太菜，还有扩欧的一堆应用看不懂，如果大佬您强的话，可以看看

随便给点题

poj 青蛙的约会 P1516 青蛙的约会

NOIP2017day1,T1 小凯的疑惑

P1762 偶数

P4777 【模板】扩展中国剩余定理（EXCRT）

$ $ 谢谢观赏，给个赞呗qwq