一、理论
1.1 多重共线性
1.2 T检验
二、回归模型
2.1 线性回归模型
适用于自变量X和因变量Y为线性关系,具体来说,画出散点图可以用一条直线来近似拟合。随机误差服从多元高斯分布。模型有几个基本假设:自变量之间无多重共线性;随机误差随从0均值,同方差的正态分布;随机误差项之间无相关关系。参数使用最小二乘法进行估计。假设检验有两个,一个是参数的检验,使用t检验;另一个是整个模型的检验,使用F检验,在构造F统计量时,需要把模型的平方和进行分解,会使用到方差分析。
2.2 线性混合模型
我的理解为在线性模型中加入随机效应项。
2.3 广义线性模型
广义线性模型,是为了克服线性回归模型的缺点出现的,是线性回归模型的推广。
首先自变量可以是离散的,也可以是连续的。离散的可以是0-1变量,也可以是多种取值的变量。
与线性回归模型相比较,有以下推广:
(1)随机误差项不一定服从正态分布,可以服从二项、泊松、负二项、正态、伽马、逆高斯等分布,这些分布被统称为指数分布族。
(2)引入联接函数。因变量和自变量通过联接函数产生影响,联接函数满足单调,可导。常用的联接函数
1 Y= X*beta
2 Y=ln(X*beta)
3 Y= 根号(X*beta)
4 ln(Y/(1-Y))=X*beta
根据不同的数据,可以自由选择不同的模型。大家比较熟悉的Logit模型就是使用Logit联接、随机误差项服从二项分布得到模型。
三、实例分析
logistic回归是假设链接函数为logi,参数为二项分布的广义线性分布,所以他的求偏导形式和最小二乘的一样。
广义线性模型(GLM)。这种模型是把自变量的线性预测函数当作因变量的估计值。在机器学习中,有很多模型都是基于广义线性模型的,比如传统的线性回归模型,最大熵模型,Logistic回归,softmax回归,等等。今天主要来学习如何来针对某类型的分布建立相应的广义线性模型。
3.1广义线性模型的认识
首先,广义线性模型是基于指数分布族的,而指数分布族的原型如下
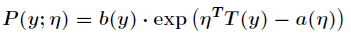
其中 为自然参数,它可能是一个向量,而
为自然参数,它可能是一个向量,而 叫做充分统计量,也可能是一个向量,通常来说
叫做充分统计量,也可能是一个向量,通常来说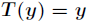 。
。
实际上线性最小二乘回归和Logistic回归都是广义线性模型的一个特例。当随机变量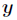 服从高斯分布,那么
服从高斯分布,那么
得到的是线性最小二乘回归,当随机变量 服从伯努利分布,则得到的是Logistic回归。
服从伯努利分布,则得到的是Logistic回归。
那么如何根据指数分布族来构建广义线性模型呢? 首先以如下三个假设为基础
(1)给定特征属性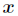 和参数
和参数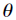 后,
后, 的条件概率
的条件概率 服从指数分布族,即
服从指数分布族,即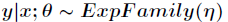 。
。
(2)预测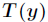 的期望,即计算
的期望,即计算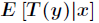 。
。
(3)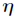 与
与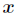 之间是线性的,即
之间是线性的,即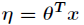 。
。
在讲解利用广义线性模型推导最小二乘和Logistic回归之前,先来认识一些常见的分布,这是后面的基础。
3.2 常见概率分布的认识
(1)高斯分布
关于高斯分布的内容我就不再多讲了,如果把它看成指数分布族,那么有

对比一下指数分布族,可以发现
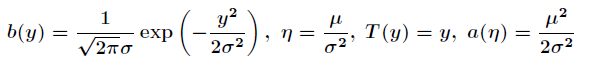
所以高斯分布实际上也是属于指数分布族,线性最小二乘就是基于高斯分布的。
(2)伯努利分布
伯努利分布又叫做两点分布或者0-1分布,是一个离散型概率分布,若伯努利实验成功,则伯努利随机变
量取值为1,如果失败,则伯努利随机变量取值为0。并记成功的概率为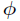 ,那么失败的概率就是
,那么失败的概率就是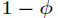 ,
,
所以得到其概率密度函数为
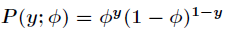
如果把伯努利分布写成指数分布族,形式如下
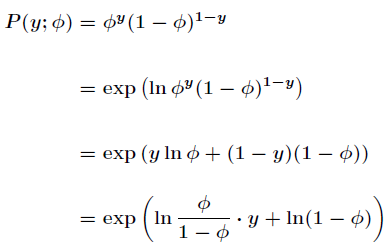
对比指数分布族,有
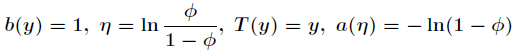
Logistic回归就是基于伯努利分布的,之前的Sigmoid函数,现在我们就可以知道它是如何来的了。如下
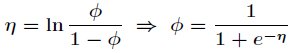
如果
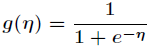
那么 叫做正则响应函数,而
叫做正则响应函数,而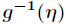 叫做正则关联函数。
叫做正则关联函数。
(3)泊松分布
泊松分布是一种离散型概率分布,其随机变量 只能取非负整数值0,1,2,... 且其概率密度函数为
只能取非负整数值0,1,2,... 且其概率密度函数为

其中参数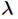 是泊松分布的均值,也是泊松分布的方差,表示单位时间内随机事件的平均发生率。在实际
是泊松分布的均值,也是泊松分布的方差,表示单位时间内随机事件的平均发生率。在实际
的实例中,近似服从泊松分布的事件有:某电话交换台收到的呼叫,某个网站的点击量,来到某个公共
汽车站的乘客,某放射性物质发射出的粒子,显微镜下某区域内的白血球等计数问题。
关于概率论中的分布主要介绍这几个,其中还有很多分布都属于指数分布族,比如伽马分布,指数分布,多
元高斯分布,Beta分布,Dirichlet分布,Wishart分布等等。根据这些分布的概率密度函数可以建立相
应的模型,这些都是广义线性模型的一个实例。
http://blog.csdn.net/acdreamers/article/details/44663091
http://bbs.pinggu.org/thread-2996069-1-1.html