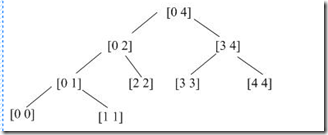
一.基础准备
自己发现:n个点的话,共n-1个非叶子节点,不过没证明过,直接看图。线段树,也叫区间树(有人说实际不一样),是一个完全二叉树,它在各个节点保存一条线段,因而常用于解决数列维护问题,树的根节点表示是“整体”的区间,左右子树分别表示这个区间的左半边和右半边。
线段树是一个满二叉树,假设共n个节点,区间为[0,n-1],那么共2*n-1个节点,深度log(2*n-1),即O(logn),这基本上述所有操作的复杂度。
线段树缺点:数列中的数不能添加或者删除。
查询的时候为什么也需要hidden(root)操作?看区间修改,估计是因为当用户修改一个区间的值时,如果连同其子孙全部修改,则改动的节点数必定会远远超过O(log n)个。因而,如果要想把区间修改操作也控制在O(log n)的时间内,只修改O(log n)个节点的信息就成为必要。然后如果要用到区间的子区间的时候,我们才去真正更新!
hidden(root)里为什么不更新id本身和?因为add函数最后一行已经更新。
hidden函数里st.node[root<<1].delta += st.node[root].delta为什么连加呢?因为可能上次查询没执行到改点,而且由于更新并未更新子节点,所以连加。
以上总结纯属个人观点,如有错误,还请指正。
二.Java实现
以POJ3468为例,直接那我的代码去AC吧。
1: /*2: * 1.我知道错误在哪啦,节点编号不能从0开始,否则左子树编号始终是03: * 2.root<<1 +1 前面必须加括号,通过打印节点发现全是2的幂4: * 3.增量必须是long,否则wa5: */6: import java.io.InputStreamReader;7: import java.util.Scanner;8:9: /*10: * n个点的话,共n-1个非叶子节点,11: * 我认为这个很重要,12: */13: public class Main {14:15: static int N = 400000;16: static Node node[] = new Node[N];17:18: public static void main(String[] args) {19: //必须放在main内20: for(int i=0; i<N; i++) {21: node[i] = new Node();22: }23: new ST().go();24: }25: }26:27: class Node {28: int left;29: int right;30: long sum;31: long delta;32:33: public Node() {34: this.delta = 0;35: this.sum = 0;36: }37: }38:39: class ST {40: String str;//判断是询问还是增加41: int a,b,c;42: long ans = -1;43: Scanner sc = new Scanner(new InputStreamReader(System.in));44: int n,m;//n个数据,m次询问45: int array[];46: Main st = new Main();//为了用node数组47:48: public void go() {49: n = sc.nextInt();50: m = sc.nextInt();51: array = new int[n+1];52: for(int i=1; i<n+1; i++) {53: array[i] = sc.nextInt();54: }55: buildTree(1,array,1,n);56: //printTree(1);57: for(int i=0; i<m; i++) {58: str = sc.next();59: a = sc.nextInt();60: b = sc.nextInt();61:62: if(str.equals("Q")) {63: ans = query(1,a,b);64: System.out.println(ans);65: }else {66: c = sc.nextInt();67: //System.out.println(a+" "+b+" "+c);68: add(1,a,b,c);69: }70: }71: }72:73: private void buildTree(int root, int[] array,int left,int right) {74: st.node[root].left = left;75: st.node[root].right = right;76: if(left==right) {77: st.node[root].sum = array[left];78: st.node[root].delta = 0;79: return ;80: }81: int mid = (left+right)>>1;82: //注意:中值在左子树83: buildTree(root<<1, array, left, mid);84: buildTree((root<<1)+1, array, mid+1, right);85: //下面这句别忘了,就是更新父节点的值,注意不是连加86: st.node[root].sum = st.node[root<<1].sum + st.node[(root<<1)+1].sum;87: }88:89: private long query(int root, int a, int b) {90: /*91: * n个点的话,共n-1个非叶子节点,所以传过来的92: * 范围可直接与节点编号比较93: * 笔者认为理解这点很重要94: */95: //System.out.println(root);96: if(st.node[root].left==a&&st.node[root].right==b) {97: return st.node[root].sum;98: }99: hidden(root);100: int mid = (st.node[root].left+st.node[root].right)>>1;101: if(b<=mid) {//有等号,因为建树时mid在左子树102: return query(root<<1, a, b);103: }else if(a>mid) {104: return query((root<<1)+1, a, b);105: }else {106: return query(root<<1, a, mid) + query((root<<1)+1, mid+1, b);107: }108: }109:110: //将更新标记传递至子节点111: private void hidden(int root) {112: if(st.node[root].delta!=0) {113: st.node[root<<1].delta += st.node[root].delta;114: st.node[root<<1].sum += st.node[root].delta115: *(st.node[root<<1].right - st.node[root<<1].left + 1);116: st.node[(root<<1)+1].delta += st.node[root].delta;117: st.node[(root<<1)+1].sum += st.node[root].delta118: *(st.node[(root<<1)+1].right - st.node[(root<<1)+1].left + 1);119: //别忘了加上,否则栈溢出120: st.node[root].delta = 0;121: }122: }123: private void printTree(int i) {124: if (st.node[i].left != 0) {125: printTree(2 * i);126: System.out.print(i+":"+"[" + st.node[i].left + "," + st.node[i].right + "] ");127: printTree(2 * i + 1);128: }129: }130: private void add(int root, int a, int b, int c) {131: if (st.node[root].left == a && st.node[root].right == b) {// 找到操作区间了132: st.node[root].delta += c; // 标记133: st.node[root].sum += c * (b - a + 1);134: return;135: }136: hidden(root);137: int mid = (st.node[root].left + st.node[root].right)>>1;138: if (b <= mid) {139: add(root * 2, a, b, c);140: } else if (a > mid) {141: add(root * 2 + 1, a, b, c);142: } else {143: add(root * 2, a, mid, c);144: add(root * 2 + 1, mid + 1, b, c);145: }146: st.node[root].sum = st.node[root * 2].sum + st.node[2 * root + 1].sum;// 更新父节点147: }148: }