并查集是一种用来解决查询合并的数据结构,支持O(1)find/O(1)union。
并查集可以使用下图来理解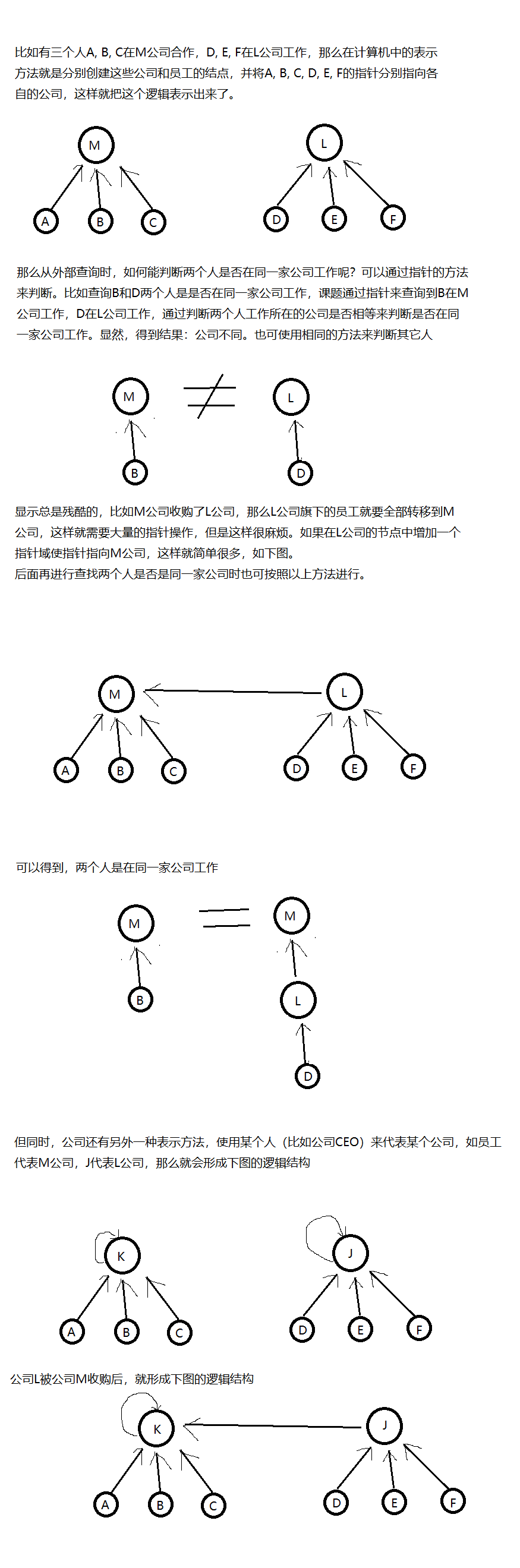
并查集的直观理解就如上图。
并查集主要也有两个功能:1.查询两个结点是否在同一家集合;2.进行合并集合
并查集的数据结构
并查集并不是像set, map, unordered_set, unordered_map这样有专门的数据结构来构建。
我们可以简单的将这个并查集使用普通数组或者哈希表就能来表示。这个并查集的数据结构从一定程度上可以视为是图。
在这里,我们使用图的哈希表(使用数组的哈希标来表示)来表示,共有8个结点,下面的行是每个结点的父结点。
| A | B | C | D | E | F | K | J |
| K | K | K | J | J | J | K | K |
并查集不需要专门的数据结构来表示,使用数组或者哈希表就能够来表示。上面是使用数组来表示的,此时数组称为father数组。
并查集可以干什么
1.判断在不在同一个集合中
find操作
会提供一个find函数,我们给定一个点,这个函数会给出这个点的代表。比如我们给出上述员工D,find函数会找到代表M或者K。
这样就可以通过find函数来找到两个点的代表是否相同来判断出这两个点是否在同一集合。
模板代码如下
1 //模板1,路径压缩之后的代码,时间复杂度为O(1) 2 int find(int x){ 3 if(father[x] == x) 4 { 5 return x; 6 }; 7 return father[x] = find(father[x]); 8 } 9 10 //模板2,时间复杂度为O(n) 11 int find(int x){ 12 if(father[x] == x) 13 { 14 return x; 15 } 16 return find(father[x]); 17 }
上述的find函数的时间复杂度是O(n).
那么我们就需要对这个路径进行压缩
如图所示
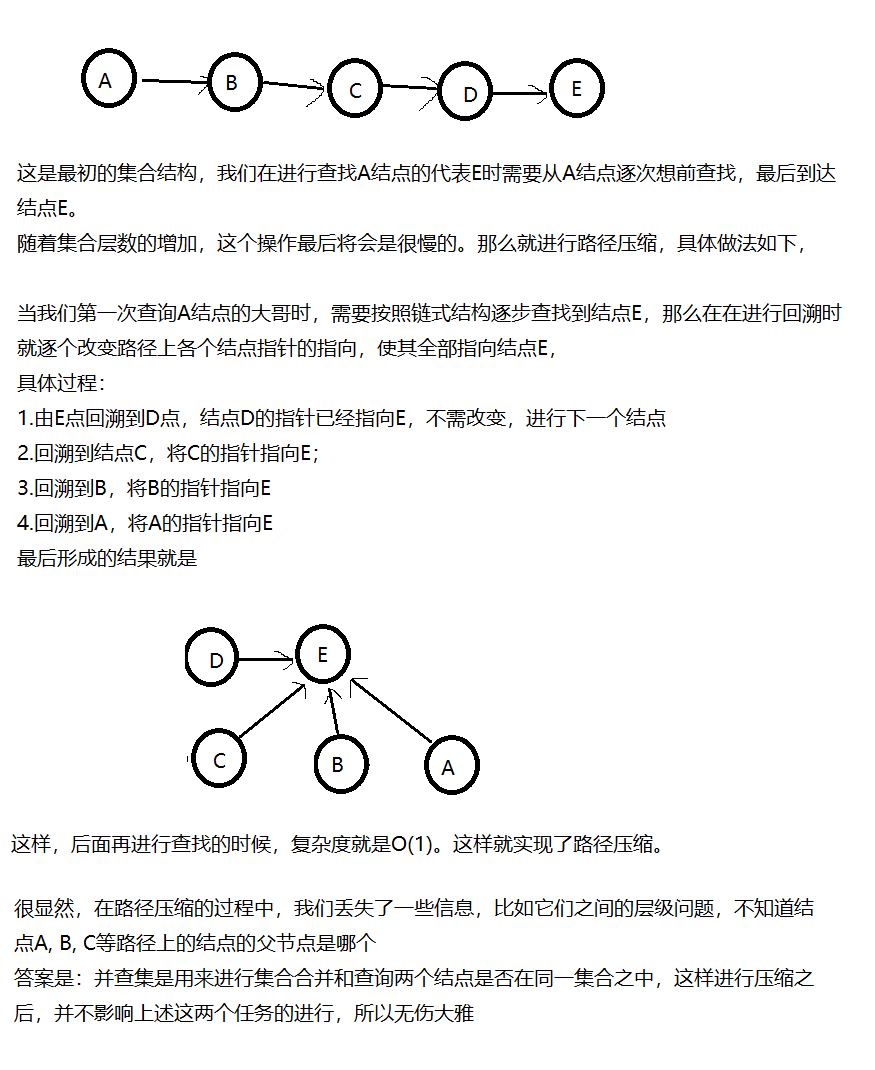
2.关于集合合并
union操作
注意:合并只是老大哥之间的合并,与下面的小弟没有关系。可以由前面的示意图可知
void union(int a, int b){ int root_a = find(a); int root_b = find(b); if(root_a != root_b){ father[root_a] = root_b; } }
由于查找的时间复杂度是O(n),所以这个合并union操作时间复杂度也是O(n)。那么经过路径压缩之后时间复杂渡就会成为O(1)。
//并查集完整模板 class UnionFind{ private: int father[1024]; public: int find(int x){ if(father[x] == x){ return x; } //带路径压缩的写法为 //return father[x] = find(father[x]); return find(father[x]); } void union(int a, int b){ int root_a = find(a); int root_b = find(b); if(root_a != root_b) { father[root_a] = root_b; } } }
遇到图的问题,就可以向并查集上去靠,这是因为图相互连接的问题就是并查集的问题。怎么看图与并查集的关系呢?
首先我们把图中所有的点都想像成为一个孤立的点的点的集合,比如一张图中共有编号为1, 2, 3, 4, 5的几个点,那么就想象成共有这么几个点的集合。那么这个图就初始化为
| 1 | 2 | 3 | 4 | 5 |
| 1 | 2 | 3 | 4 | 5 |
此时各个点都是孤立的,点的父结点都是自己本身。
那么我们现在进行1和2之间的连接,合并后图就成为1-2, 3, 4, 5.这个步骤也可以视为是只有一个元素1的集合与只有一个元素2的集合的合并,此时并查集表就成为
| 1 | 2 | 3 | 4 | 5 |
| 2 | 2 |
3 |
4 | 5 |
此时再进行查找是就得到1-2和2-2,这样就相当于建立了1,2之间的连接。
接着将2与4之间按照上述方法连接,图就成为了1-2-4, 3, 5。并查集的数组就是
| 1 | 2 | 3 | 4 | 5 |
| 2 | 2 | 3 | 2 | 5 |
这样查询1,4之间是否连接时,就有1-2,4-2最终可以确定1.4之间是连接的。
同时,假如我们建立了1-2-4的连接,那么我们此时若再建立1-4的连接吗,答案是不需要的
在建立之前我们需要检查他们各自的老大哥的结点是否一致,也就是检查是否在同一集合之中,若是,则不需要修改指向,若不是,再修改。
比如:1-2-4中1的老大哥是4,4的老大哥是他本身,这样我们就不需要再建立1-4之间的连接,也就不需要进行任何的操作。