leetcode 5 Longest Palindromic Substring

DP解

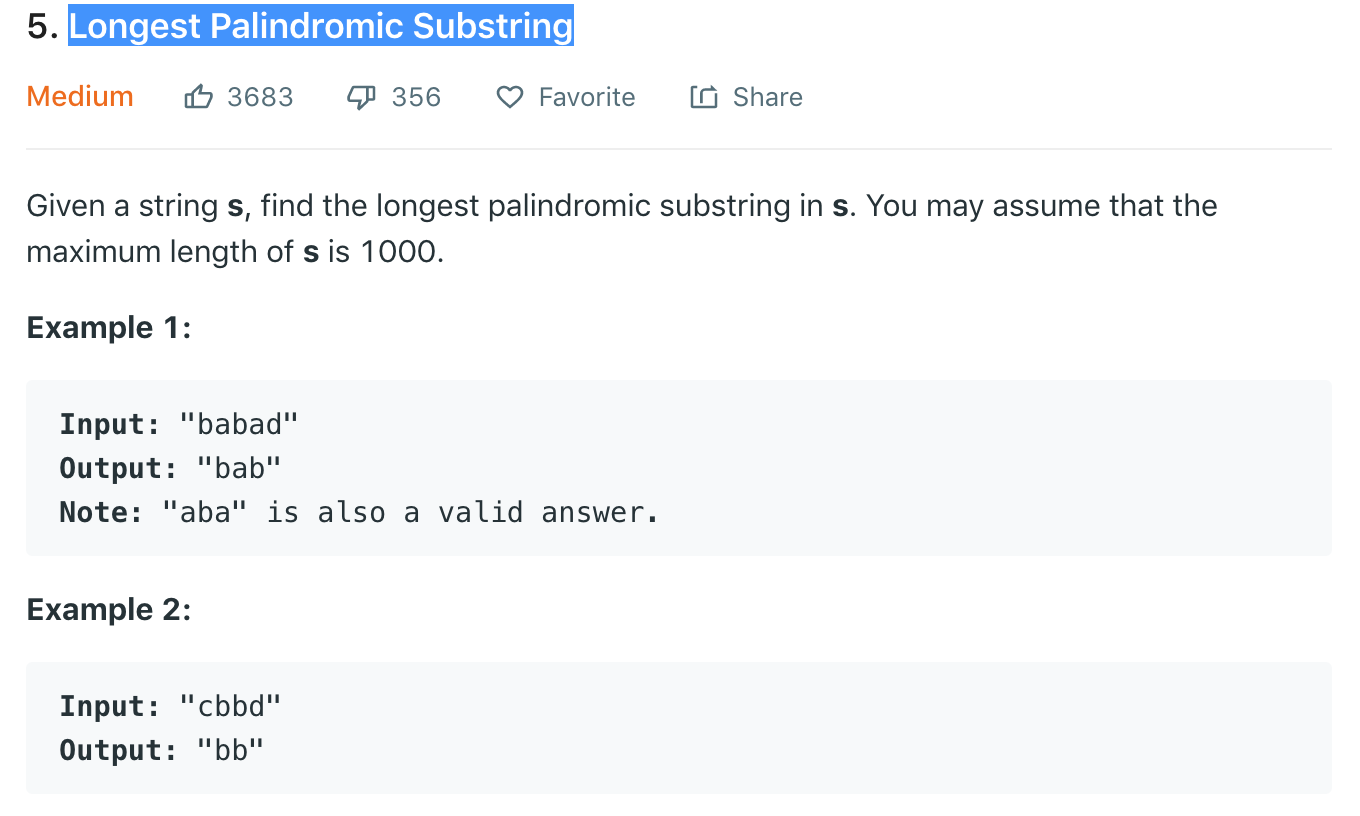
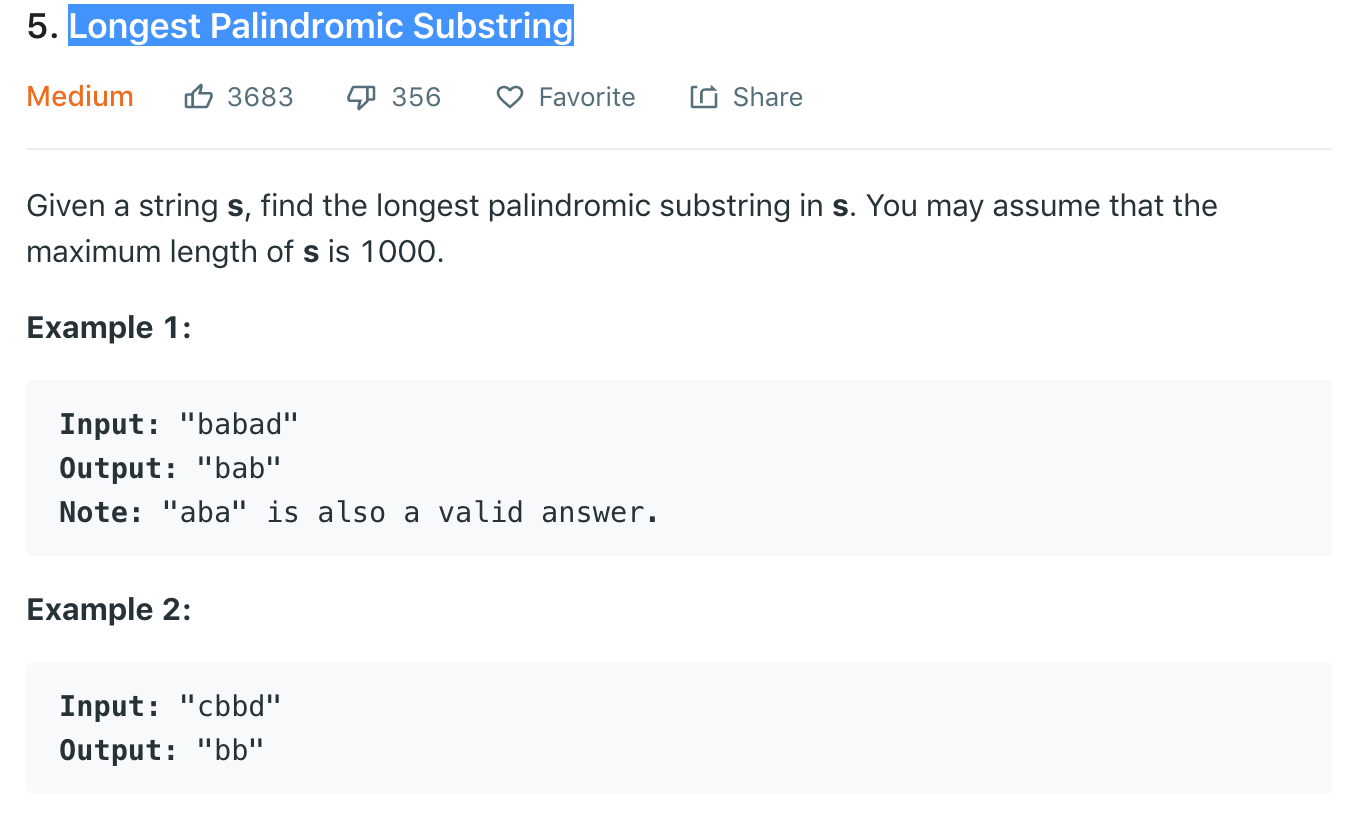
dp[i][j] ：表示s(i~j)是否可以构成回文串，是一个boolean二维数组

dp[i][j] = dp[i+1][j-1] && s.charAt(i) == s.charAt(j)

注意当子串长度为0，1，2时不需要考虑i+1~j-1，只需要考虑i和j是否相等

所以上式改为dp[i][j] = (dp[i+1][j-1] || j-i < 3) && s.charAt(i) == s.charAt(j)

还有一点，当i=j=0时，j-1会造成数组越界，i=j=s.length()-1是，i+1也会造成越界

我们可以利用java判断语句的特性，即A||B，当A为真，B不执行

调整上式顺序j-i < 3 || dp[i+1][j-1]，因为这两种情况j-i都<3

class Solution {
    public String longestPalindrome(String s) {
        boolean[][] dp = new boolean[s.length()][s.length()];
        String res = "";
        
        for(int i=s.length()-1; i>=0; i--){
            for(int j=i; j<s.length(); j++){
                dp[i][j] = s.charAt(i) == s.charAt(j) && (j-i < 3 || dp[i+1][j-1]);
                if(res.length() < j-i+1 && dp[i][j])
                    res = s.substring(i, j+1);
            }
        }
        return res;
    }
}