二进制高效位运算

数独

数独是介绍位运算的好例子，运用位运算和不运用效率差别还是挺大的。我们先看数独需求:

1、当前数字所在行数字均含1-9，不重复

2、当前数字所在列数字均含1-9，不重复

3、当前数字所在宫（即3x3的大格）数字均含1-9，不重复（宫，如下图每个粗线内是一个宫）

、

常规算法

若是我们采用常规方式的，每填写一个数字，需要检查当前行、列，宫中其他位置是否有重复数字，极端情况下需要循环27（3*9）次来进行检查，我们看下常规算法下check

	int check(int sp) {
	   // 檢查同行、列、九宮格有沒有相同的數字，若有傳回 1
	   int fg= 0 ;
	   if(!fg) fg= check1(sp, startH[sp], addH) ;   // 檢查同列有沒有相同的數字
	   if(!fg) fg= check1(sp, startV[sp], addV) ;   // 檢查同行有沒有相同的數字
	   if(!fg) fg= check1(sp, startB[sp], addB) ;   // 檢查同九宮格有沒有相同的數字
	   return(fg) ;
	}

	int check1(int sp, int start, int *addnum) {
	   // 檢查指定的行、列、九宮格有沒有相同的數字，若有傳回 1
	   int fg= 0, i, sp1  ;
	   //万恶的for循环
	   for(i=0; i<9; i++) {
	      sp1= start+ addnum[i] ;
	      if(sp!=sp1 && sudoku[sp]==sudoku[sp1]) fg++ ;
	   }
	   return(fg) ;
	}

这个效率是否很吓人，每次填写一个就需要check27次，有木有check一次的算法？当然有了，采用位运算，一次搞定。来我们看下位运算的思路:

位运算

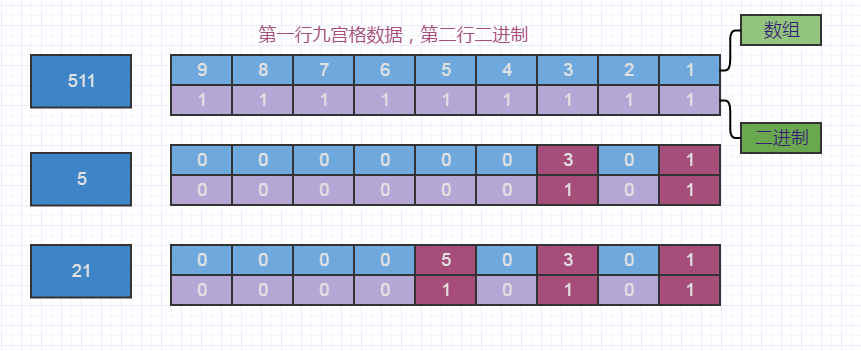
我们看上图所示，单个行（或者列、宫）数据，都是有1-9共9个数字，我们统称为九宫数字。若是我们采用二进制，以九宫数字充当二进制数据的位坐标,采用9位的二进制就可以与之一一对应，位上有数据，标识为1，无数据标识为0，如此一个正数就能解决一行九宫数据状态，无需需存一个数组。

比如 看图中深红色部分，当前九宫数据中已经有1和3，那么二进制右起第一位和第三位标识为1，一个数字5就可以存下当前行（或者列、宫）数组状态了,如若数字为511表明，所有的九宫数字都用完了，如图第一行。

check一个数字是否已经被占用了，可以采取位运算来获取二进制的右数第k位来查看是否是1，若是1，表明指定数字已经被占用了。我们看下具体check算法:

	// sp 是当前位置索引，indexV 行索引，indexH 列索引，indexB九宫格索引
	int check(int sp,int indexV,int indexH,int indexB) {
	   // 检查同行、列、九宮格沒有用到的数字，若已经用过返回 1
		int status = statusV[indexV]|statusH[indexH]|statusB[indexB];
		//9个数字都被用了
		if (status>=STATUS_MAX_VALUE)
		{
			return 1;
		}
		int number=sudoku[sp];
		//取右数第k位,若是1表明这个值已经存在了
		return status>>(number-1)&1;
	}

	// 行、列、宫二进制数据指定位置标记为1
	int markStatus(int indexV,int indexH,int indexB,int number){
		if (number<1)
		{
			return 0;
		}
		//把右数第k(从1计数)位变成1 
   	  	statusV[indexV]|=(1<<(number-1));
    	statusH[indexH]|=(1<<(number-1));
    	statusB[indexB]|=(1<<(number-1));
	}

我们以以下图例位置举例，如何获得当前位置可以填取的数字

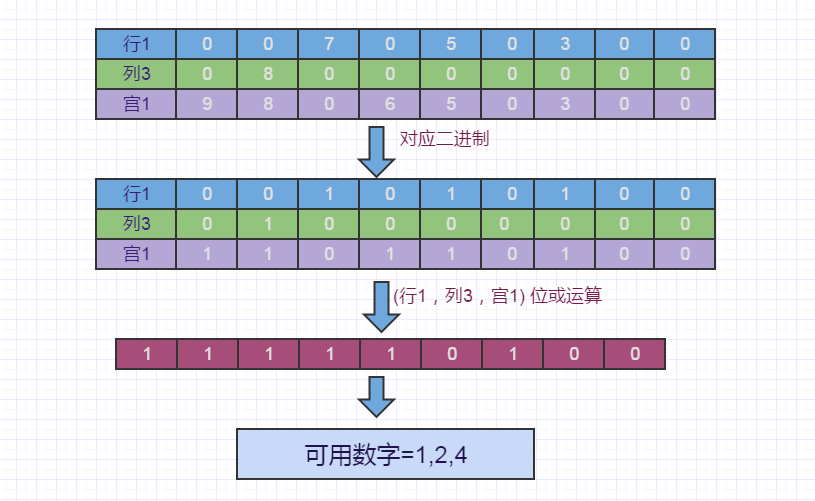
可以看到2个位运算就解决了检查可用数字的操作了，而之前常规算法，需要用27次查找才可以获取到。当然了这个算法还可以优化，比如采用启发式DFS，搜索可用数字，速度更快，感兴趣可点击这里。

常规算法和位运算算法C语言代码，我已经上传码云了，想了解的点击下面链接，自行去查看去。（常规算法google的）

地址: 常规算法数独，位运算版本数独

 基础

位操作符

符号	含义	规则
&	与	两个位都为1时，结果为1
|	或	有一个位为1时，结果为1
^	异或	0和1异或0都不变，异或1则取反
~	取反	0和1全部取反
<<	左移	位全部左移若干位，高位丢弃，低位补0
>>	算术右移	位全部右移若干位，，高位补k个最高有效位的值
>>	逻辑右移	位全部右移若干位，高位补0

注意:

1、位运算只可运用于整数，对于float和double不行。

2、另外逻辑右移符号各种语言不太同，比如java是>>>。

3、位操作符的运算优先级比较低，尽量使用括号来确保运算顺序。比如1&i+1,会先执行i+1再执行&。

应用实例

很棒的应用实例，你可以mark一下，方便以后对照使用。

1、混合体

位运算实例

位运算	功能	示例
x >> 1	去掉最后一位	101101->10110
x << 1	在最后加一个0	101101->1011010
x << 1 | 1	在最后加一个1	101101->1011011
x | 1	把最后一位变成1	101100->101101
x & -2	把最后一位变成0	101101->101100
x ^ 1	最后一位取反	101101->101100
x | (1 << (k-1))	把右数第k位变成1	101001->101101,k=3
x & ~ (1 << (k-1))	把右数第k位变成0	101101->101001,k=3
x ^(1 <<(k-1))	右数第k位取反	101001->101101,k=3
x & 7	取末三位	1101101->101
x & (1 << k-1)	取末k位	1101101->1101,k=5
x >> (k-1) & 1	取右数第k位	1101101->1,k=4
x | ((1 << k)-1)	把末k位变成1	101001->101111,k=4
x ^ (1 << k-1)	末k位取反	101001->100110,k=4
x & (x+1)	把右边连续的1变成0	100101111->100100000
x | (x+1)	把右起第一个0变成1	100101111->100111111
x | (x-1)	把右边连续的0变成1	11011000->11011111
(x ^ (x+1)) >> 1	取右边连续的1	100101111->1111
x & -x	去掉右起第一个1的左边	100101000->1000
x&0x7F	取末7位	100101000->101000
x& ~0x7F	是否小于127	001111111 & ~0x7F->0
x & 1	判断奇偶	00000111&1->1

2、交换两数

int swap(int a, int b)  
{  
    if (a != b)  
    {  
        a ^= b;  
        b ^= a;  
        a ^= b;  
    }  
}  

3、求绝对值

int abs(int a)  
{  
    int i = a >> 31;  
    return ((a ^ i) - i);  
}  

4、二分查找32位整数前导0个数

int nlz(unsigned x)
{
   int n;

   if (x == 0) return(32);
   n = 1;
   if ((x >> 16) == 0) {n = n +16; x = x <<16;}
   if ((x >> 24) == 0) {n = n + 8; x = x << 8;}
   if ((x >> 28) == 0) {n = n + 4; x = x << 4;}
   if ((x >> 30) == 0) {n = n + 2; x = x << 2;}
   n = n - (x >> 31);
   return n;
}

5、二进制逆序

int reverse_order(int n){

  n = ((n & 0xAAAAAAAA) >> 1) | ((n & 0x55555555) << 1);
  n = ((n & 0xCCCCCCCC) >> 2) | ((n & 0x33333333) << 2);
  n = ((n & 0xF0F0F0F0) >> 4) | ((n & 0x0F0F0F0F) << 4);
  n = ((n & 0xFF00FF00) >> 8) | ((n & 0x00FF00FF) << 8);
  n = ((n & 0xFFFF0000) >> 16) | ((n & 0x0000FFFF) << 16);

  return n;
}

6、 二进制中1的个数

 unsigned int BitCount_e(unsigned int value) {
        unsigned int count = 0;
        // 解释下下面这句话代码，这句话求得两两相加的结果，例如 11 01 00 10
        // 11 01 00 10 = 01 01 00 00 + 10 00 00 10，即由奇数位和偶数位相加而成
        // 记 value = 11 01 00 10，high_v = 01 01 00 00， low_v = 10 00 00 10
        // 则 value = high_v + low_v，high_v 右移一位得 high_v_1，
        // 即 high_v_1 = high_v >> 1 = high_v / 2
        // 此时 value 可以表示为 value = high_v_1 + high_v_1 + low_v，
        // 可见 我们需要 high_v + low_v 的和即等于 value - high_v_1
        // 写简单点就是 value = value & 0x55555555 + (value >> 1) & 0x55555555;
        value = value - ((value >> 1) & 0x55555555);

        // 之后的就好理解了
        value = (value & 0x33333333) + ((value >> 2) & 0x33333333);
        value = (value & 0x0f0f0f0f) + ((value >> 4) & 0x0f0f0f0f);
        value = (value & 0x00ff00ff) + ((value >> 4) & 0x00ff00ff);
        value = (value & 0x0000ffff) + ((value >> 8) & 0x0000ffff);
        return value;

        // 另一种写法，原理一样，原因在最后一种解法中有提到
        //value = (value & 0x55555555) + (value >> 1) & 0x55555555;
        //value = (value & 0x33333333) + ((value >> 2) & 0x33333333);
        //value = (value & 0x0f0f0f0f) + ((value >> 4) & 0x0f0f0f0f);
        //value = value + (value >> 8);
        //value = value + (value >> 16);
        //return (value & 0x0000003f);
    }