最近四五年,互联网行业似乎总是绕不开社交网络这个概念。无论是旗舰级别的传说中的facebook、LinkedIn,还是如雨后春笋般冒出来的各种团购和微博网站,全都或多或少地体现着SNS(社会网络服务)的特色。这些五花八门的产品,在丰富我们业余生活的同时,也为研究者提供了大量珍贵的数据。以往只能依靠有限的调研或模拟才能进行的社会网络分析(SNA),现在具备了大规模开展和实施的条件。国内著名而典型的SNS网站“人人网”,最近依靠上市新闻重新赢得了大家的关注。本文基于人人网的好友关系数据,应用统计分析软件R做了社会网络分析的一些尝试。
注:网络边界的确定,是社会网络分析的关键而困难的步骤。由于数据获取的限制,本文分析的对象限制于作者的好友。也就是说,本文分析的网络是作者自己的好友圈子,读者看了这些分析结果或许会觉得索然无味,感兴趣的同学可以分析一下自己的社交网络,看看是否会有类似的结果。
2013-03-23 做了相应的R包,分别用于新浪微博和校内网,本文的脚本不再做更新。
一、读取数据
之所以选择人人网作为分析的对象,很重要的一点原因在于其数据获取较为便利。本文读取数据的过程借助了一款命令行浏览器cURL,这个浏览器在R中可以用RCurl包实现,简要的中文介绍建议参考medo的《R不务正业之RCurl》。通过RCurl的简单编程,我们可以在R中实现登录人人网、发布状态以及读取页面数据等功能。
人人网好友列表页面的url为http://friend.renren.com/GetFriendList.do?curpage=0&id=****,其中curpage为页码参数,id为相应的用户。通过对id与curpage做简单的循环,作者读取了自己(陈逸波)的所有好友以及好友的好友。(读取数据的R代码见文末附件。)
用上述代码读取到的数据集记为friend_all,该数据有如下的格式:
set.seed(13) friend_all[sample(1:nrow(friend_all), 10), ]
u0 id0 u1 id1 68282 沈叶 229657865 邢凤婷 238382560 19358 吴昊宸 115975869 吴玥 250106135 18406 叶敏佳MO小沫 222288430 官兴华 32503437 7782 李彬 54598688 鱼化石 323984442 57464 牛智 1411553595 谢諹 221389295 1833 马天云 23157153 张立 227738255 222150 刘雯欢 227317115 李嫣 334590411 278125 陈长虹 236145500 李利文 249059215 135239 高涛 248013976 宋阳阳 247196544 18214 蒋鸿章 35702214 华明明 226037245
其中,第一行数据表示“沈叶”与“邢凤婷”是好友关系,id0与id1为相应的用户id。需要注意的是人人网中不可避免地会出现同名用户的情况,因此id才是用户的唯一标识。
二、绘制简单的好友关系网络图
本文分析的焦点集中于作者的好友之间形成的网络,因此考虑做网络图来直观地展示网络的结构。
首先,从上述读取到的数据集中筛选出希望分析的子集。这个子集包含了两个条件:
(1)网络中没有作者自己(否则会呈现以作者为中心的分布,失去了分析的意义);
(2)网络中的用户都是作者自己的好友。
uid = "41021031"
## "41021031"是用户的uid,在读取数据的代码中可以自动获取
friend_all[, 2] = as.character(friend_all[, 2])
friend_all[, 4] = as.character(friend_all[, 4])
tmp1 = friend_all[friend_all[, 2] == uid, ]
tmp2 = friend_all[(friend_all[, 2] != uid) &
(friend_all[, 4] %in% tmp1[, 4]), c(2, 4)]
## tmp1 = tmp1[tmp1[, 4] %in% c(tmp2[, 1], tmp2[, 2]), ]
## 这句话本意是用来去掉那些孤立点。在后面用degree的方式做掉了。
然后就是直接利用igraph包的做图功能绘制相应的网络图。考虑前面提到的用户同名情况,直接用id来做后续的分析。
library(igraph)
people = data.frame(id = tmp1[, 4], name = tmp1[, 3])
gg = graph.data.frame(d = tmp2, directed = F, vertices = people)
is.simple(gg)
gg = simplify(gg)
## 去掉重复的连接
is.simple(gg)
dg = degree(gg)
gg = subgraph(gg, which(dg > 0) - 1)
## 去掉孤立点
## png("net_simple.png", width = 500, height = 500)
par(mar = c(0, 0, 0, 0))
set.seed(14)
plot(gg, layout = layout.fruchterman.reingold, vertex.size = 5, vertex.label = NA,
edge.color = grey(0.5), edge.arrow.mode = "-")
## dev.off()
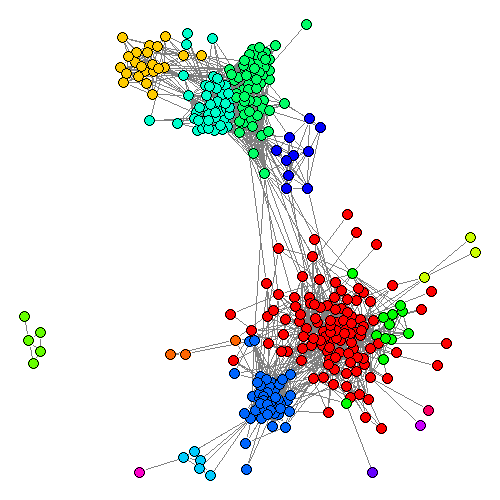
从图中可以直观地看出,作者的好友网络存在一定的人群分割,可以尝试对这个网络进行一些分析以提取出其中相对独立的子群(或者称为社群)。
三、子群分割
信息的分类和过滤是社会网络服务的一项特征,例如人人网对好友关系有一套自己的分类方式,用户可以自行对好友进行分组,从而对信息的收发做分组的管理。但是作为用户却未必能够养成并保持这种分组的习惯(例如作者自己就从来没有对好友做过分组)。与此同时我们揣测,作为真实关系的线上反映,人人网的好友网络是能够自动呈现出一定的人群分割的,而在社会网络分析中,对网络成分的分析也确实是一项重点。通过分析网络的结构,提取出其中的子群,能够让我们更好地理解这个网络的组成方式,从而更好地管理和利用信息流。
寻找子群的算法有很多,igraph包提供了若干函数以实现对网络子群的搜索,本文采用了其中的walktrap.community()函数,更多细节及其他算法可以查看帮助文档。
为了在网络图中展示这些子群,我们采用不同的颜色来标记他们。
com = walktrap.community(gg, steps = 5)
subgroup = split(com$labels, com$membership)
## subgroup
V(gg)$sg = com$membership + 1
V(gg)$color = rainbow(max(V(gg)$sg))[V(gg)$sg]
## png("net_walktrap.png", width = 500, height = 500)
par(mar = c(0, 0, 0, 0))
set.seed(14)
plot(gg, layout = layout.fruchterman.reingold, vertex.size = 5,
vertex.color = V(gg)$color, vertex.label = NA, edge.color = grey(0.5),
edge.arrow.mode = "-")
## dev.off()
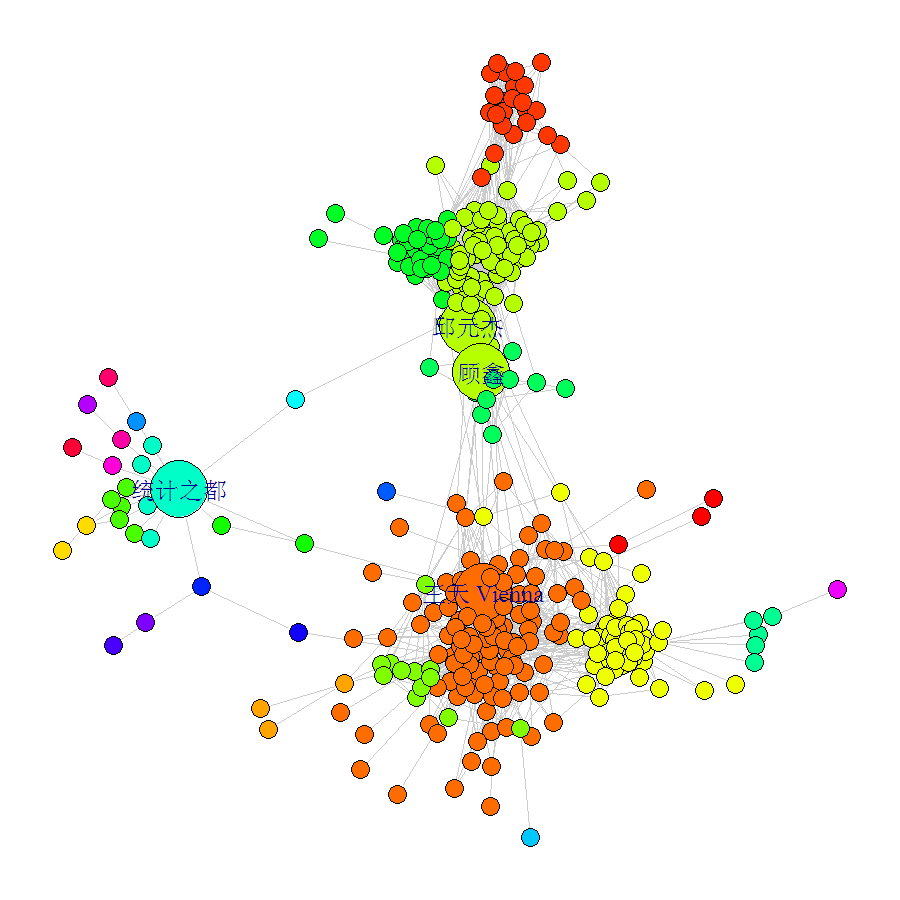
从图中可以直观地看出好友网络已经被划分为若干相对独立的子群。这也与我们对人人网(尤其是其前身校内网)的直观理解相符合——人人网的好友关系基本都是真实线下关系的反映,很自然地可以划分为初中同学、高中同学、大学同学,等等(例如网络的上半部分为小学及中学的同学,下半部分为大学同学,而左侧的五个节点,那是统计之都的同学们。)。
具体地看一下划分得到的子群,就能够更好地理解子群的含义。作者挑出了比较典型的几个子群,其中包括:
“实验室同学”(子群9)
subgroup[[9]]
[1] "周莉" "杨志昌" "潘伟" "卢进文" "胡刚"
“校内论坛上某版版友”(子群7)
subgroup[[7]]
[1] "曲文君" "翟传鑫" "梁玮" "单广宇" [5] "花木马leeear" "王昉" "李典" "陈侃" [9] "王祎萍" "牛智" "郗旺" "何志嵩"
“高中学弟学妹”(子群11)
subgroup[[11]]
[1] "邹舒怡" "封启云" "何非" "朱亚希" "陈平" [6] "洪怡君" "程功" "李常然" "朱燕^^Jue" "周飏 Ivy"
“统计之都”(子群8)
subgroup[[8]]
[1] "魏太云" "邓一硕" "吴云崇" "高涛" "统计之都"
其他子群还包括“大学同学(数学系)”、“大学同学(非数学系)”等等,不一而足(甚至能够区分高中的不同班级的同学)。因此可以认为上述算法得到的子群划分是合理且有意义的。
更进一步地,可以对照网络图来考察各个子群成员的分布情况。例如大学数学系同学(下方蓝色点)的链接较为紧密,而非数学系的大学同学(主要是校内论坛CC98上的朋友,下方红色点)的分布则相对分散。通过网络密度可以定量地印证这一点:
## 数学系 sg10=subgraph(gg,V(gg)[sg==10]) ## 非数学系 sg1=subgraph(gg,V(gg)[sg==1]) graph.density(gg) ## [1] 0.06376068 graph.density(sg10) ## [1] 0.5883441 graph.density(sg1) ## [1] 0.1223607
四、起到中介作用的那些好友
在社会网络分析中,对节点的中介作用有一个经典的刻画叫做“中间度”。中间度衡量了节点作为中介的程度,当网络中某个个体的中间度较大时,我们认为它在很大程度上起到了中介和沟通的作用。常用的中间度的定义是betweenness()函数能够简单地计算网络中各个节点的中间度。
V(gg)$bte = betweenness(gg, directed = F)
## png("net_betweenness.png", width = 500, height = 500)
par(mar = c(0, 2, 0, 0))
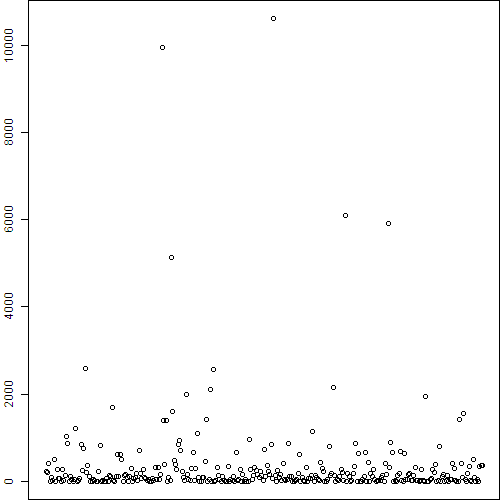
plot(V(gg)$bte)
## dev.off()
根据得到的中间度散点图,我们人为地选择了3000作为分界点,选取中间度高于3000的节点并在图形中利用节点的大小展示出来。
V(gg)$size = 5
V(gg)[bte>=3000]$size = 15
## 当然啦这里的3000换成分位数之类的会更合理
V(gg)$label=NA
V(gg)[bte>=3000]$label=V(gg)[bte>=3000]$name
V(gg)$cex=1
V(gg)[bte>=3000]$cex=2
## png("net_walktrap_betweenness.png", width = 500, height = 500)
par(mar = c(0, 0, 0, 0))
set.seed(14)
plot(gg, layout = layout.fruchterman.reingold, vertex.size = V(gg)$size,
vertex.color = V(gg)$color, vertex.label = V(gg)$label,
vertex.label.cex=V(gg)$cex, edge.color = grey(0.5),
edge.arrow.mode = "-")
## dev.off()
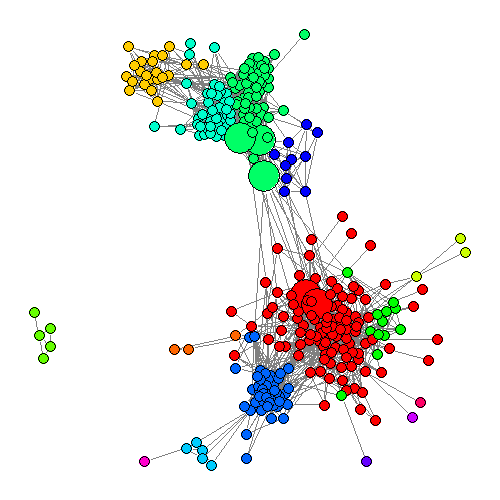
从图中也可以直观地看出,中间度最高的5个节点,确实位于中介的地位。
具体看这5个节点:
V(gg)[bte>=3000]
Vertex sequence: [1] "邱元杰" "娄谦之" "王子涵" "刘波" "顾鑫"
对这5个节点,基本上都有比较合理的解释,其中有三个人是“高中校友”兼“大学校友”,而另外两个则沟通了“网络好友”与“大学好友”。
五、基于好友关系的一种简单的推荐
最后,我们也做了基于好友关系的好友推荐,推荐的逻辑与人人网自身的推荐逻辑相同:根据共同好友的数量来进行推荐。在具体实现的时候,仍然需要考虑用户同名的情况。
tmp3 = friend_all[!(friend_all[, 4] %in%
friend_all[friend_all[, 2] == "41021031", 4]), ]
listall = sort(table(tmp3[, 4]), dec = T)
top = names(listall[1:20])
tmp4 = tmp3[tmp3[, 4] %in% top, 3]
top20 = sort(table(tmp4), dec = T)
top20
周科 邹碧筠Phoebe 査小狮 韩晶磊 陆丽娜 55 49 42 41 41 焦丽萍 蔡锡真 高晨 鲁锦彪 张洁 40 39 39 38 38 张明珠 范莉悦 钱咏邠 薛俊波悟空 周迪 38 37 37 37 37 陈素 蒋莹 唐甜 费逸 王丽涵 36 36 36 35 35
这个推荐的结果与人人网的推荐基本一致(因为逻辑相同嘛),以下是人人网的一些推荐截图:
上述推荐的机制较为简单,但是在拥有大量真实关系的网络中,推荐的效率还是比较高的。当然,我们也可以开展对文本与行为的挖掘,以得到超越真实线下关系的推荐,但本文尚未做这方面的尝试。