经过一系列的预处理,包括缺失值填充,中位数计算以及归一化,我们的数据终于可以用啦。
下面我们就来分析一下new population和old population的个体是否有差异表达基因。
判断一个基因是否差异表达有许多方法,最早使用的就是看log ratio的绝对值是否大于2,这种方法早已废弃。
下一个想到的也许是t-test,诚然t-test可以统计地判断一个基因是否差异表达,但是对于有数千数万基因的芯片来说,会有很高的错误发现率(False Discovery Rate, FDR),如果 p value < 0.05,则10000个基因里有500个基因实际没有差异表达而被误认为是差异表达。因此t-test方法需要改进。
于是 Westfall & Young (1993) 提出了Step-down maxT and minP multiple testing procedures,大意就是比较几个group间有没有差异基因表达,就通过随机置换这些group的标记,相当于随机互换group的成员,模拟一个空分布(null distribution),以此计算调整后的p value,这个方法可以极大的减小Family-wise Error Rate (FWER).
以下分析就使用Step-down maxT and minP multiple testing procedures,需要求助于Bioconductor的multtest package的mt.maxT()函数。具体用法可通过help(mt.maxT)查看。
source("http://bioconductor.org/biocLite.R")
biocLite("multtest")
library(multtest)
classlabel<-c(0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1)
maxttt<-mt.maxT(norm_log_btw_array,classlabel,B=100000)
默认随机置换次数B=10000,对于microarray来说B应该比10000大很多,所以这里取B=100000
以下是画图:
rawp<-maxttt$rawp[order(maxttt$index)]
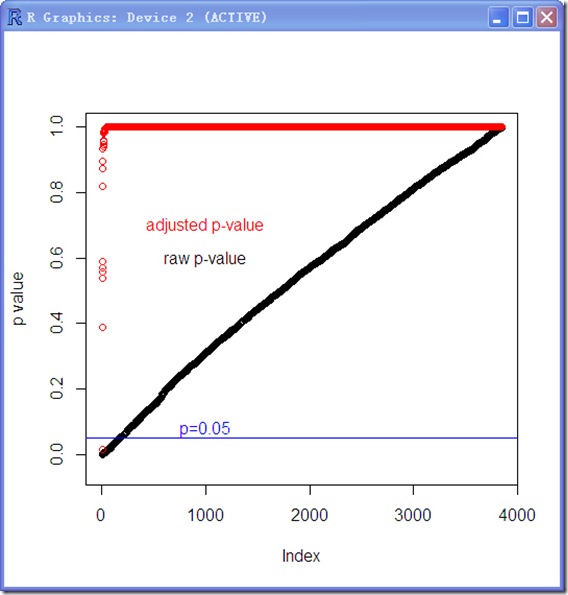
plot(sort(rawp),type='p',col=1,ylim=c(-0.05,1.00),ylab='p value')
lines(sort(maxttt$adjp),type='p',col='red')
#min adj-p: sort(maxttt$adjp)[1] 0.0163
#rawp: >sort(rawppp)[170] [1] 0.0493 > sort(rawppp)[171] [1] 0.0502 170个raw p小于0.05
abline(h=0.05,col='blue')
text(1000,c(0.6,0.7),labels=c('raw p-value','adjusted p-value'),col=c('black','red'))
text(1000,0.08,labels='p=0.05',col='blue')
可见调整后只有一个基因的p value小于0.05,而未调整的有170个基因的p value小于0.05,可以说虽然此方法降低了错误发现率,但是也导致了很高的False negative.
此外可以考虑使用multtest package的mt.rawp2adjp()函数,这个函数可以通过”Bonferroni”, “Holm”, “Hochberg”, “SidakSS”, “SidakSD”, “BH”, “BY”等方法调整p value,不过对我们的数据来说都过于严格了。
procs<-c("Bonferroni","Holm","Hochberg","SidakSS","SidakSD","BH","BY")
adjps<-mt.rawp2adjp(rawp,procs)
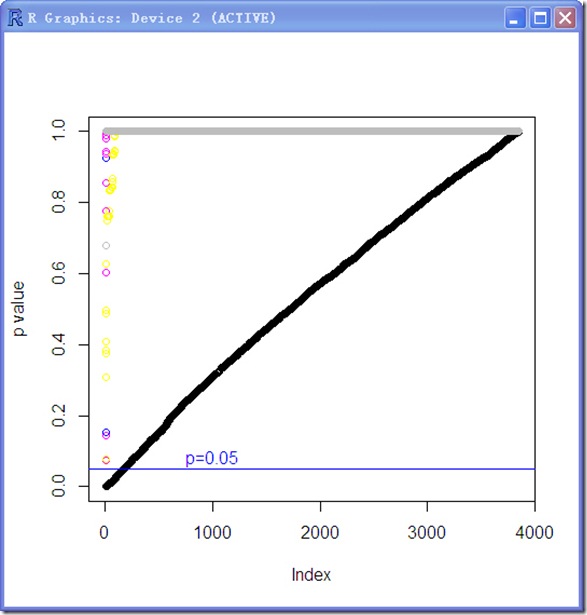
plot(sort(adjps$adjp[,1]),ylab='p value')
for (i in 2:8){
points(sort(adjps$adjp[,i]),col=i)
}
abline(h=0.05,col='blue')
text(1000,0.08,labels='p=0.05',col='blue')
因此可以考虑不这么严格的SAM (Significance Analysis of Microarrays)分析。有兴趣的请看参考资料。。
参考资料:
课堂讲义:Differential expression. Identifying differentially expressed genes — notions on multiple testing and p-value adjustments.
Dudoit, S., Yang, Y.H., Speed, T.P., and Callow, M.J. (2002), Statistical methods for identifying differentially expressed genes in replicated cDNA microarray experiments, Statistica Sinica 12(1):111-139.
Dudoit S., Shaffer J.P., Boldrick J.C. (2003). Multiple hypothesis testing in microarray experiments, Statistical Science, 18(1): 71-103.
Efron B., Tibshirani, R., Storey J.D., and Tusher V. (2001), Empirical Bayes analysis of a microarray experiment, Journal of the American Statistical Association 96:1151-1160.
SAM (Significance Analysis of Microarrays)相关:Tusher, V.G., Tibshirani, R., and Chu, G. (2001) Significance analysis of microarrays applied to the ionizing radiation response, PNAS 98:5116-5121.
FDR相关:Storey J.D. (2002), A direct approach to false discovery rates, JRSS-B 64(3):479-498.
from : http://azaleasays.com/tag/r/