LOJ#2320 生成树计数

解：讲一个别的题解里我比较难以理解的地方，就是为什么可以把这两个东西合起来看成某一个连通块指数是2m而别的指数都是m。

其实很好理解，但是别人都略过了......把后面的∑提到∏的前面，然后展开，也可以理解成把∏塞到∑里面。

然后我们就发现对于每个生成树，我们其实有n种选择，分别把某个块的次数变成2m，且每种选择都作为一棵生成树计入贡献，且这回的贡献，一个树内部各个块全部是乘积的形式。

---

发现贡献与度数有关，又要求所有生成树，于是考虑prufer序列。

如何看待每个点是一个连通块？就是对于一种生成树，实际方案要乘上(点数^度数)。代表每条边连哪个点。

这样一个生成树的权值是这个东西：

接下来考虑钦定每个连通块的度数。在prufer序列中每个数的出现次数是度数-1，于是令d_i = d_i - 1

首先要把这些点在prufer中排列一下，于是有：

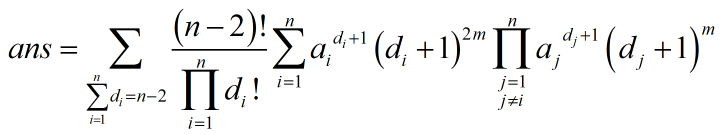
接下来一顿操作，把di！塞到∏里面，(n-2)!提出来，就有个式子。

然后考虑生成函数，推荐这个。

关于求等幂和这个式子，实在是不理解...

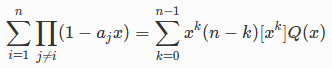
这东西还要我用vector写多项式......

然后搞来搞去，不管了...

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <vector>

typedef long long LL;
const int N = 100010;
const LL MO = 998244353, G = 3;
typedef LL arr[N << 2];
typedef std::vector<LL> Poly;

arr A, B, exp_t, inv_t, inv_t2, f, g, h, p, ex;
int r[N << 2], n;
LL m, a[N], pw[N];

inline LL qpow(LL a, LL b) {
    a %= MO;
    LL ans = 1;
    while(b) {
        if(b & 1) ans = ans * a % MO;
        a = a * a % MO;
        b = b >> 1;
    }
    return ans;
}

inline void prework(int n) {
    static int R = 0;
    if(R == n) return;
    R = n;
    int lm = 1;
    while((1 << lm) < n) lm++;
    for(int i = 0; i < n; i++) r[i] = (r[i >> 1] >> 1) | ((i & 1) << (lm - 1));
    return;
}

inline void NTT(LL *a, int n, int f) {
    prework(n);
    for(int i = 0; i < n; i++) {
        if(i < r[i]) std::swap(a[i], a[r[i]]);
    }
    for(int len = 1; len < n; len <<= 1) {
        LL Wn = qpow(G, (MO - 1) / (len << 1));
        if(f == -1) Wn = qpow(Wn, MO - 2);
        for(int i = 0; i < n; i += (len << 1)) {
            LL w = 1;
            for(int j = 0; j < len; j++) {
                LL t = a[i + len + j] * w % MO;
                a[i + len + j] = (a[i + j] - t) % MO;
                a[i + j] = (a[i + j] + t) % MO;
                w = w * Wn % MO;
            }
        }
    }
    if(f == -1) {
        LL inv = qpow(n, MO - 2);
        for(int i = 0; i < n; i++) a[i] = a[i] * inv % MO;
    }
    return;
}

inline void mul(const LL *a, const LL *b, LL *c, int n) {
    int len = 1;
    while(len < n + n) len <<= 1;
    memcpy(A, a, n * sizeof(LL)); memset(A + n, 0, (len - n) * sizeof(LL));
    memcpy(B, b, n * sizeof(LL)); memset(B + n, 0, (len - n) * sizeof(LL));
    NTT(A, len, 1); NTT(B, len, 1);
    for(int i = 0; i < len; i++) c[i] = A[i] * B[i] % MO;
    NTT(c, len, -1);
    memset(c + n, 0, (len - n) * sizeof(LL));
    return;
}

inline Poly mul(const Poly &a, const Poly &b) {
    int len = 1, lena = a.size(), lenb = b.size();
    while(len < lena + lenb) len <<= 1;
    Poly ans(lena + lenb - 1);
    for(int i = 0; i < lena; i++) A[i] = a[i];
    for(int i = 0; i < lenb; i++) B[i] = b[i];
    memset(A + lena, 0, (len - lena) * sizeof(LL));
    memset(B + lenb, 0, (len - lenb) * sizeof(LL));
    NTT(A, len, 1); NTT(B, len, 1);
    for(int i = 0; i < len; i++) A[i] = A[i] * B[i] % MO;
    NTT(A, len, -1);
    for(int i = 0; i < lena + lenb - 1; i++) ans[i] = A[i];
    return ans;
}

void Inv(const LL *a, LL *b, int n) {
    if(n == 1) {
        b[0] = qpow(a[0], MO - 2);
        b[1] = 0;
        return;
    }
    Inv(a, b, n >> 1);
    /// ans = b * (2 - a * b);
    memcpy(A, a, n * sizeof(LL)); memset(A + n, 0, n * sizeof(LL));
    memcpy(B, b, n * sizeof(LL)); memset(B + n, 0, n * sizeof(LL));
    NTT(A, n << 1, 1); NTT(B, n << 1, 1);
    for(int i = 0; i < (n << 1); i++) b[i] = B[i] * (2 - A[i] * B[i] % MO) % MO;
    NTT(b, n << 1, -1);
    memset(b + n, 0, n * sizeof(LL));
    return;
}

inline void getInv(const LL *a, LL *b, int n) {
    int len = 1;
    while(len < n) len <<= 1;
    Inv(a, b, len);
    memset(b + n, 0, (len - n) * sizeof(LL));
    return;
}

inline Poly getInv(const Poly &a) {
    int n = a.size(), len = 1;
    while(len < n) len <<= 1;
    for(int i = 0; i < n; i++) inv_t[i] = a[i];
    memset(inv_t + n, 0, (len - n) * sizeof(LL));
    getInv(inv_t, inv_t2, n);
    Poly ans(n);
    for(int i = 0; i < n; i++) ans[i] = inv_t2[i];
    return ans;
}

inline void der(const LL *a, LL *b, int n) {
    for(int i = 0; i < n - 1; i++) {
        b[i] = a[i + 1] * (i + 1) % MO;
    }
    b[n - 1] = 0;
    return;
}

inline void ter(const LL *a, LL *b, int n) {
    for(int i = n - 1; i >= 1; i--) {
        b[i] = a[i - 1] * qpow(i, MO - 2) % MO;
    }
    b[0] = 0;
    return;
}

inline void getLn(const LL *a, LL *b, int n) {
    getInv(a, inv_t, n);
    der(a, A, n);
    int len = 1;
    while(len < n + n) len <<= 1;
    memset(A + n, 0, (len - n) * sizeof(LL));
    memcpy(B, inv_t, n * sizeof(LL)); memset(B + n, 0, (len - n) * sizeof(LL));
    NTT(A, len, 1); NTT(B, len, 1);
    for(int i = 0; i < len; i++) b[i] = A[i] * B[i] % MO;
    NTT(b, len, -1);
    memset(b + n, 0, (len - n) * sizeof(LL));
    ter(b, b, n);
    return;
}

void Exp(const LL *a, LL *b, int n) {
    if(n == 1) {
        b[0] = 1;
        b[1] = 0;
        return;
    }
    Exp(a, b, n >> 1);
    /// ans = b * (1 + a - ln b)
    getLn(b, exp_t, n);
    for(int i = 0; i < n; i++) A[i] = (a[i] - exp_t[i]) % MO;
    A[0] = (A[0] + 1) % MO;
    memset(A + n, 0, n * sizeof(LL));
    memcpy(B, b, n * sizeof(LL)); memset(B + n, 0, n * sizeof(LL));
    NTT(A, n << 1, 1); NTT(B, n << 1, 1);
    for(int i = 0; i < (n << 1); i++) b[i] = A[i] * B[i] % MO;
    NTT(b, n << 1, -1);
    memset(b + n, 0, n * sizeof(LL));
    return;
}

inline void getExp(const LL *a, LL *b, int n) {
    int len = 1;
    while(len < n) len <<= 1;
    Exp(a, b, len);
    memset(b + n, 0, (len - n) * sizeof(LL));
    return;
}

inline void out(const Poly &a) {
    //printf("siz = %d ", a.size());
    for(int i = 0; i < a.size(); i++) {
        printf("%lld ", (a[i] + MO) % MO);
    }
    printf("
");
    return;
}

Poly dvd(int l, int r) {
    if(l == r) {
        Poly res(2);
        res[0] = 1; res[1] = -a[r];
        return res;
    }
    int mid = (l + r) >> 1;
    Poly ans = mul(dvd(l, mid), dvd(mid + 1, r));
    return ans;
}

inline void solve1() {
    Poly q = dvd(1, n);
    Poly p(n);
    for(int i = 0; i < n; i++) {
        p[i] = q[i] * (n - i) % MO;
    }
    p = mul(p, getInv(q));
    for(int i = 0; i < n; i++) {
        ex[i] = p[i];
        //printf("ex %d = %lld 
", i, ex[i]);
    }
    return;
}

int main() {

    scanf("%d%lld", &n, &m);
    for(int i = 1; i <= n; i++) {
        scanf("%lld", &a[i]);
    }
    ///
    solve1();

    pw[0] = 1;
    for(int i = 1; i <= n; i++) pw[i] = pw[i - 1] * i % MO;
    for(int i = 0; i < n; i++) {
        f[i] = qpow(i + 1, m) * qpow(pw[i], MO - 2) % MO;
        h[i] = qpow(i + 1, m << 1) * qpow(pw[i], MO - 2) % MO;
    }
    getInv(f, p, n);
    mul(p, h, h, n);

    getLn(f, g, n);
    for(int i = 0; i < n; i++) {
        g[i] = g[i] * ex[i] % MO;
        h[i] = h[i] * ex[i] % MO;
    }
    getExp(g, f, n);

    mul(h, f, f, n);

    LL ans = f[n - 2];
    for(int i = 1; i < n - 1; i++) ans = ans * i % MO;
    for(int i = 1; i <= n; i++) ans = ans * a[i] % MO;

    if(ans < 0) ans += MO;
    printf("%lld
", ans);

    return 0;
}