HDU5608 function

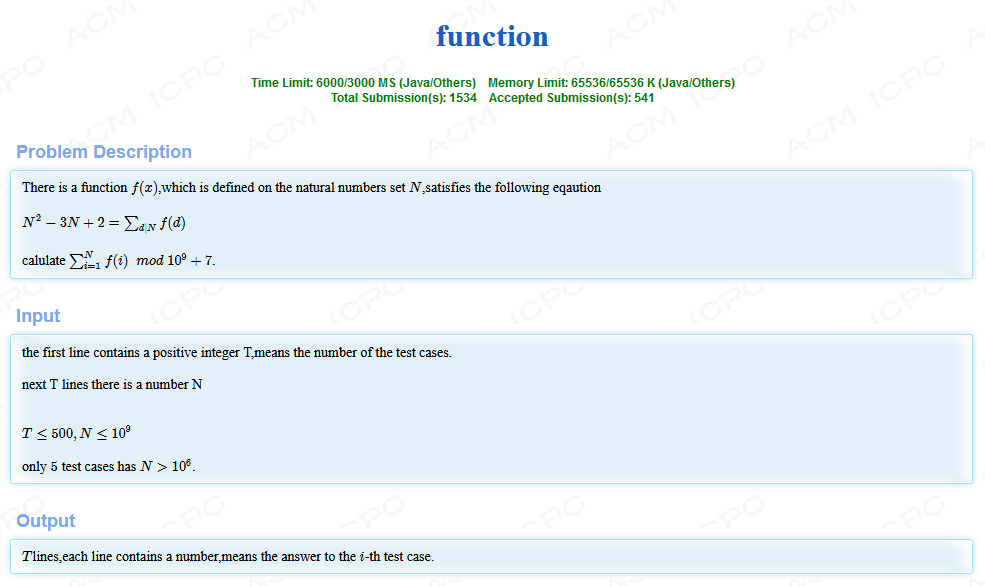
解：显然f那个式子可以反演一波，然后再推一波，最后出来了这个......

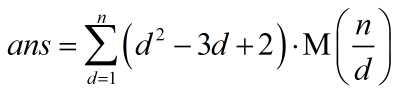
其中M是莫比乌斯函数的前缀和。虽然看起来能算...感觉很毒瘤，复杂度也不会。

正解：杜教筛的套路是对一个卷函数求前缀和，然后拆开。

于是我们直接对(i² - 3i + 2)求前缀和，之后就是一个很普通的杜教筛式子了......

如何预处理f？利用反演式子，考虑每个(i² - 3i + 2)会对哪些f有所贡献即可。复杂度调和级数。

注意long long和取模...我全程爆炸调了一晚上。

#include <cstdio>
#include <cmath>
#include <cstring>
#include <map>

typedef long long LL;
const int N = 1000010, T = 1000008;
const LL MO = 1e9 + 7, inv6 = 166666668, inv2 = 500000004, INF = 0x7f7f7f7f7f7f7f7fll;

int miu[N], p[N], top;
LL F[N], n;
std::map<LL, LL> F2;
bool vis[N];

inline LL qpow(LL a, LL b) {
    LL ans = 1;
    while(b) {
        if(b & 1) ans = ans * a % MO;
        a = a * a % MO;
        b = b >> 1;
    }
    return ans;
}

inline LL G(LL x) {
    x %= MO;
    return (((x * 2 + 1) % MO) * inv6 % MO * x % MO * ((x + 1) % MO) % MO -
    ((x + 1) % MO) * inv2 % MO * x % MO * 3 % MO + x * 2 % MO) % MO;
}

inline LL g(LL x) {
    x %= MO;
    return (x * x % MO - 3 * x % MO + 2 + MO) % MO;
}

inline void prework() {
    /// get miu
    miu[1] = 1;
    for(int i = 2; i <= T; i++) {
        if(!vis[i]) {
            p[++top] = i;
            miu[i] = -1;
        }
        for(int j = 1; j <= top && i * p[j] <= T; j++) {
            vis[i * p[j]] = 1;
            if(i % p[j] == 0) break;
            miu[i * p[j]] = -miu[i];
        }
    }
    /// getF
    for(int i = 1; i <= T; i++) {
        LL t = g(i);
        for(int j = 1; i * j <= T; j++) {
            F[i * j] += t * miu[j] % MO;
            F[i * j] = (F[i * j] % MO + MO) % MO;
        }
    }
    for(int i = 1; i <= T; i++) {
        F[i] = (F[i] + F[i - 1]) % MO;
    }
    return;
}

LL solve(LL x) {
    if(x <= 0) return 0;
    if(x <= T) return F[x];
    if(F2.count(x)) return F2[x];
    LL ans = G(x);
    for(LL i = 2, j; i <= x; i = j + 1) {
        j = x / (x / i);
        ans -= solve(x / i) * (j - i + 1) % MO;
        ans = (ans % MO + MO) % MO;
    }
    return F2[x] = ans;
}

int main() {
    int q;
    scanf("%d", &q);
    prework();
    //printf("q = %d 
", q);
    for(int i = 1; i <= q; i++) {
        //printf("i = %d q = %d 
", i, q);
        scanf("%lld", &n);
        printf("%lld
", solve(n));
    }
    return 0;
}