参考资料。
先讲几个水一点的式子热身。
求1~n每个数的约数和。
先把约数和函数拆开，然后把枚举的d提前，考虑每个d被枚举了多少次。显然d的倍数会枚举到d，所以每个d就被枚举了1~n中d的倍数次，也就是(n/d)次。
后面那个式子可以对(n/d)分块，乘上一段区间的和。复杂度sqrt(n)
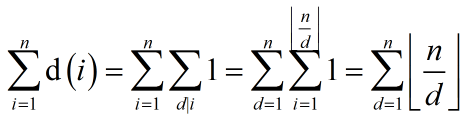
上式的简化版，不再赘述。
①式的一个变形。
首先把乘法拆开，把j提前枚举，考虑每个j被枚举了多少次(画出来是一个三角形的矩阵)。显然1~(n/j)都会枚举到j，而(n/j)+1就不会。后面的式子是一个1~t的和。
所以我们得到了一个很好玩的式子:
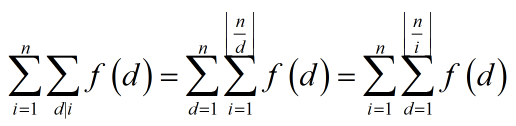
第一步转化是经典的约数提前枚举。第二步是经典的求和交换。
接下来看一看经典的杜教筛：欧拉函数前缀和。
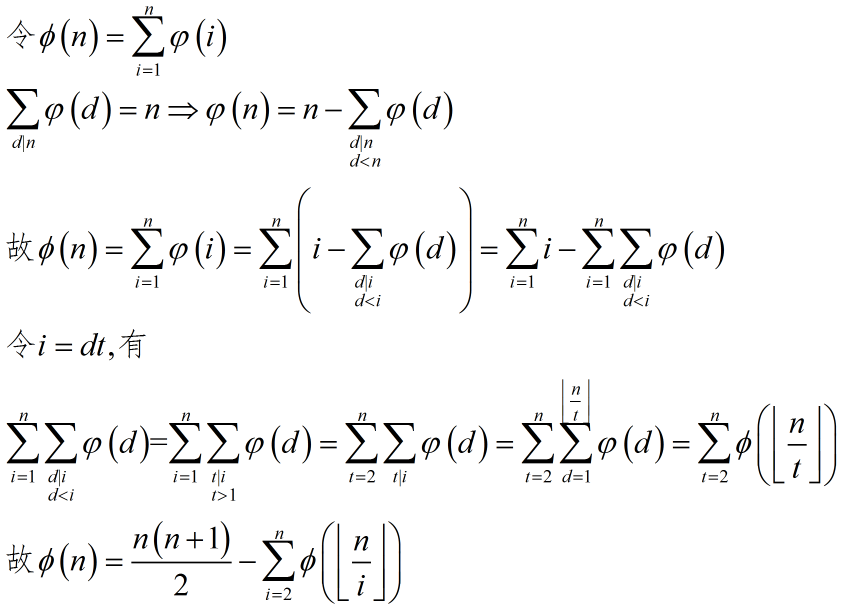
推到这一步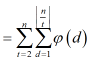
的时候还可以交换dt，但是会得到一个没啥用的式子......
这是一种naive的推法，比较大众的方法：
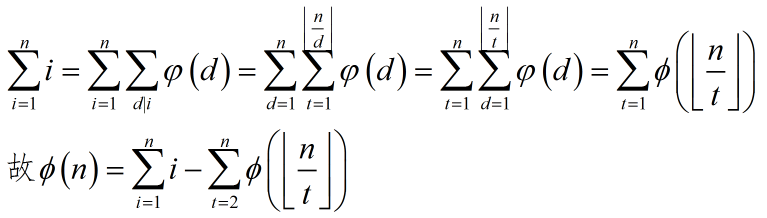
直接用上面的最终式计算，可以做到n0.75的复杂度。再预处理一波，就是n2/3了。
接下来是莫比乌斯函数前缀和：
根据刚学到的套路，找到某个函数跟它卷起来，然后对卷出来的函数求前缀和，套路一波。
代码：
1 #include <cstdio> 2 #include <algorithm> 3 #include <cmath> 4 #include <cstring> 5 6 typedef long long LL; 7 const int N = 4900010; 8 const LL INF = 0x7f7f7f7f7f7f7f7fll; 9 10 int p[N], top, miu[N], T; 11 LL Miu[N], n, miU[N]; 12 bool vis[N]; 13 14 inline void getp(int n) { 15 miu[1] = 1; 16 for(int i = 2; i <= n; i++) { 17 if(!vis[i]) { 18 p[++top] = i; 19 miu[i] = -1; 20 } 21 for(int j = 1; j <= top && i * p[j] <= n; j++) { 22 vis[i * p[j]] = 1; 23 if(i % p[j] == 0) { 24 break; 25 } 26 miu[i * p[j]] = -miu[i]; /// get miu phi when visit 27 } 28 } 29 for(int i = 1; i <= n; i++) { 30 Miu[i] = Miu[i - 1] + miu[i]; 31 } 32 return; 33 } 34 35 LL solve(LL x) { 36 //printf("T = %d ", T); 37 if(x <= 0) return 0; 38 if(x <= T) return Miu[x]; 39 if(miU[n / x] != INF) return miU[n / x]; 40 //printf("x = %lld T = %d ", x, T); 41 LL ans = 1; 42 for(LL i = 2, j; i <= x; i = j + 1) { 43 j = x / (x / i); // [i, j] 44 ans -= (j - i + 1) * solve(x / i); 45 } 46 return miU[n / x] = ans; 47 } 48 49 LL work(LL x) { 50 n = x; 51 memset(miU, 0x7f, sizeof(miU)); 52 return solve(x); 53 } 54 55 int main() { 56 LL l, r; 57 scanf("%lld%lld", &l, &r); 58 T = (int)pow(r, 2.0/3.0); 59 60 getp(T); 61 printf("%lld ", work(r) - work(l - 1)); 62 63 return 0; 64 }
1 #include <cstdio> 2 #include <cstring> 3 #include <cmath> 4 5 typedef long long LL; 6 const LL MO = 1000000007; 7 const int N = 5000010; 8 9 int T, p[N], top, phi[N]; 10 bool vis[N]; 11 LL n, Phi[N], phI[N], inv2; 12 13 inline void getp(int n) { 14 phi[1] = 1; 15 for(int i = 2; i <= n; i++) { 16 if(!vis[i]) { 17 p[++top] = i; 18 phi[i] = i - 1; 19 } 20 for(int j = 1; j <= top && i * p[j] <= n; j++) { 21 vis[i * p[j]] = 1; 22 if(i % p[j] == 0) { 23 phi[i * p[j]] = phi[i] * p[j] % MO; 24 break; 25 } 26 phi[i * p[j]] = phi[i] * (p[j] - 1) % MO; 27 } 28 } 29 for(int i = 1; i <= n; i++) { 30 Phi[i] = (Phi[i - 1] + phi[i]) % MO; 31 } 32 return; 33 } 34 35 LL solve(LL x) { 36 if(x <= 0) return 0; 37 if(x <= T) return Phi[x]; 38 if(phI[n / x] != -1) return phI[n / x]; 39 LL ans = (x + 1) % MO * (x % MO) % MO * inv2 % MO; 40 for(LL i = 2, j; i <= x; i = j + 1) { 41 j = x / (x / i); 42 ans -= (j - i + 1) % MO * solve(x / i) % MO; 43 ans = (ans % MO + MO) % MO; 44 } 45 return phI[n / x] = ans; 46 } 47 48 inline LL work(LL x) { 49 n = x; 50 memset(phI, -1, sizeof(phI)); 51 return solve(x); 52 } 53 54 int main() { 55 inv2 = (MO + 1) / 2; 56 LL x; 57 scanf("%lld", &x); 58 T = pow(x, 2.0 / 3); 59 getp(T); 60 printf("%lld ", work(x)); 61 return 0; 62 }
1 #include <cstdio> 2 #include <cmath> 3 #include <tr1/unordered_map> 4 5 typedef long long LL; 6 const int N = 1000010, T = 1000000; 7 8 std::tr1::unordered_map<LL, LL> phI; 9 std::tr1::unordered_map<LL, int> miU; 10 int p[N], top, phi[N], miu[N], Miu[N], n; 11 LL Phi[N]; 12 bool vis[N]; 13 14 inline void getp(int n) { 15 phi[1] = miu[1] = 1; 16 for(int i = 2; i <= n; i++) { 17 if(!vis[i]) { 18 p[++top] = i; 19 miu[i] = -1; 20 phi[i] = i - 1; 21 } 22 for(int j = 1; j <= top && i * p[j] <= n; j++) { 23 vis[i * p[j]] = 1; 24 if(i % p[j] == 0) { 25 phi[i * p[j]] = phi[i] * p[j]; 26 break; 27 } 28 phi[i * p[j]] = phi[i] * (p[j] - 1); 29 miu[i * p[j]] = -miu[i]; 30 } 31 } 32 for(int i = 1; i <= n; i++) { 33 Phi[i] = Phi[i - 1] + phi[i]; 34 Miu[i] = Miu[i - 1] + miu[i]; 35 } 36 return; 37 } 38 39 LL getPhi(int x) { 40 if(x <= 0) return 0; 41 if(x <= T) return Phi[x]; 42 if(phI.count(x)) return phI[x]; 43 LL ans = x * (x + 1ll) / 2; 44 for(unsigned i = 2, j; i <= x; i = j + 1) { 45 j = x / (x / i); 46 ans -= (j - i + 1) * getPhi(x / i); 47 } 48 return phI[x] = ans; 49 } 50 51 int getMiu(int x) { 52 if(x <= 0) return 0; 53 if(x <= T) return Miu[x]; 54 if(miU.count(x)) return miU[x]; 55 int ans = 1; 56 for(unsigned i = 2, j; i <= x; i = j + 1) { 57 j = x / (x / i); 58 ans -= (j - i + 1) * getMiu(x / i); 59 } 60 return miU[x] = ans; 61 } 62 63 int main() { 64 getp(T); 65 int q; 66 scanf("%d", &q); 67 for(int i = 1; i <= q; i++) { 68 scanf("%d", &n); 69 printf("%lld %d ", getPhi(n), getMiu(n)); 70 } 71 72 return 0; 73 }
这个sum是卡常神题......千万别做.....这TM比紫荆花之恋还难卡，洛谷我死活过不去，弃疗了。
关于欧拉函数，公式是这个，所以考虑括号内乘上一个因数时，函数值对应的乘那个因数就好了。
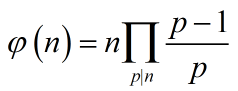
f(x) = x2 的前缀和: F(x) = x(x + 1)(2x + 1) / 6
f(x) = x3 的前缀和: F(x) = (1+2+3+...+x)2
感觉这道题是杜教筛的时候，就千万不能过度推式子...要搞个g出来卷一卷......
一般要找g的话先把h(x)写出来，然后考虑g化成什么能够轻易求前缀和。
跟反演或者别的什么结合的时候，一般先推式子，推到某一步的时候发现还差个前缀和就OK了，这时候再考虑怎么杜教筛。
接下来是例题。