之前做的时候没想出来...现在来数学推导一波。
题意:从n个木棒中选出4个拼成一个矩形,使得 (周长)2/面积 最小。
解:设矩形宽a长b。我们要最小化下面这个式子:
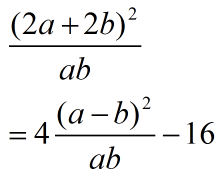
去掉常数,不妨设b = a + len,则化为下式:
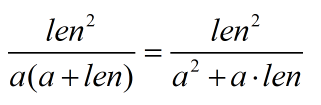
取倒数,也就是最大化下式:

显然对于每个确定的a,len越小越好。所以直接取相邻的即可。
好像还有一种推导方法......
原式可直接化为a/b + b/a,这就是个耐克函数双钩函数,让a/b趋近1也就是a=b,所以a和b越接近越好。
之前做的时候没想出来...现在来数学推导一波。
题意:从n个木棒中选出4个拼成一个矩形,使得 (周长)2/面积 最小。
解:设矩形宽a长b。我们要最小化下面这个式子:
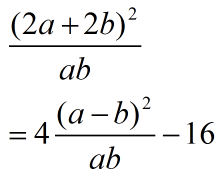
去掉常数,不妨设b = a + len,则化为下式:
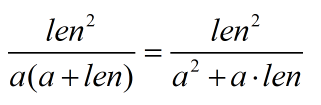
取倒数,也就是最大化下式:

显然对于每个确定的a,len越小越好。所以直接取相邻的即可。
好像还有一种推导方法......
原式可直接化为a/b + b/a,这就是个耐克函数双钩函数,让a/b趋近1也就是a=b,所以a和b越接近越好。