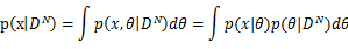在进行参数估计的时候, 常用到最大似然估计,其形式很简单,对于含有N个样本的训练数据集DN,假设样本独立同分布,分布参数为 ,则似然概率定义如下:
,则似然概率定义如下:
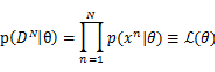
简单说就是参数为 时训练集出现的概率,然后我们根据不同的分布形式求导,得到参数
时训练集出现的概率,然后我们根据不同的分布形式求导,得到参数 的最有值使得似然概率最大。
的最有值使得似然概率最大。
贝叶斯学习过程不同之处在于,一开始并不试图去求解一个最优的参数值,而是假设参数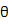 本身符合某个分布,即先验概率p(
本身符合某个分布,即先验概率p(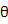 )(例如高斯分布,只要知道均值和方差就能确定下来),利用训练数据集所得到的信息就可以得到参数
)(例如高斯分布,只要知道均值和方差就能确定下来),利用训练数据集所得到的信息就可以得到参数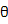 的条件概率分布p(
的条件概率分布p(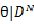 )(条件概率的用途后面揭晓)。
)(条件概率的用途后面揭晓)。
由贝叶斯公式,我们可以得到:

再根据前面的独立性假设:
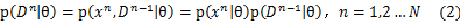
将公式(2)带入公式(1)中,得到:
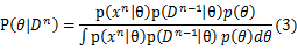
再次使用贝叶斯公式,我们发现:
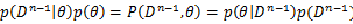
所以:
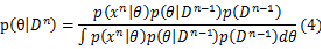
这里有必要指出的是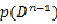 与参数
与参数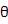 是独立的,可以这样理解,对于一个已知的分布形式,我们假设了
是独立的,可以这样理解,对于一个已知的分布形式,我们假设了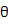 的分布类型:
的分布类型: ,积分过程中去掉了参数,所以它本身是与
,积分过程中去掉了参数,所以它本身是与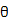 独立的,则公式(4)可以简化成:
独立的,则公式(4)可以简化成:
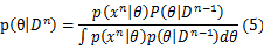
整个推导过程并没有涉及到参数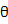 的具体分布形式,可见公式(5)对于各种分布函数是普遍适用的,该公式体现的是参数的条件概率密度的迭代更新过程,显然,更新的起始点:
的具体分布形式,可见公式(5)对于各种分布函数是普遍适用的,该公式体现的是参数的条件概率密度的迭代更新过程,显然,更新的起始点: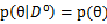 ,没有任何数据的时候,我们所有的就是先验概率。
,没有任何数据的时候,我们所有的就是先验概率。
最后提一下为什么要求解参数的条件概率密度,在分类问题中,给定属于某一类的训练数据集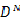 ,对于某一个输入模式,我们要确定类条件概率密度,也就是p(x|DN)
,对于某一个输入模式,我们要确定类条件概率密度,也就是p(x|DN)
由贝叶斯公式
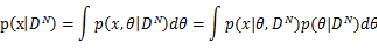
前面提过,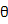 与
与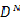 相互独立,则
相互独立,则 ,所以
,所以