KNN及其改进算法的python实现

一、 马氏距离

我们熟悉的欧氏距离虽然很有用，但也有明显的缺点。它将样品的不同属性（即各指标或各变量）之间的差别等同看待，这一点有时不能满足实际要求。例如，在教育研究中，经常遇到对人的分析和判别，个体的不同属性对于区分个体有着不同的重要性。因此，有时需要采用不同的距离函数。
　　如果用dij表示第i个样品和第j个样品之间的距离，那么对一切i，j和k，dij应该满足如下四个条件：
    ①当且仅当i=j时，d_ij=0
　　②d_ij＞0
　　③d_ij＝d_ji（对称性）
　　④d_ij≤d_ik＋d_kj（三角不等式）
显然，欧氏距离满足以上四个条件。满足以上条件的函数有多种，本节将要用到的马氏距离也是其中的一种。
　　第i个样品与第j个样品的马氏距离d_ij用下式计算：
　　　　d_ij =(x _i 一x _j)'S^-1(x _i一x_j)
　　其中，x _i 和x _j分别为第i个和第j个样品的m个指标所组成的向量，S为样本协方差矩阵。
　　马氏距离有很多优点。它不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关；由标准化数据和中心化数据(即原始数据与均值之差）计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。它的缺点是夸大了变化微小的变量的作用。举例说明：

两个样本：
His1 = {3,4,5,6}
His2 = {2,2,8,4}
它们的均值为：
U = {2.5, 3, 6.5, 5}
协方差矩阵为：
S =
| 0.25  0.50  -0.75  0.50  |
| 0.50  1.00  -1.50  1.00  | 
|-0.75  -1.50    2.25  -1.50  |
| 0.50  1.00  -1.50  1.00  |
其中S(i,j)={[His1(i)-u(i)]*[His1(j)-u(j)]+[His2(i)-u(i)]*[His2(j)-u(j)]}/2
下一步就是求出逆矩阵S^(-1)
马氏距离 D=sqrt{[His1-His2] * S^(-1) * [(His1-His2)的转置列向量]}
1）马氏距离的计算是建立在总体样本的基础上的，这一点可以从上述协方差矩阵的解释中可以得出，也就是说，如果拿同样的两个样本，放入两个不同的总体中，最后计算得出的两个样本间的马氏距离通常是不相同的，除非这两个总体的协方差矩阵碰巧相同；
2）在计算马氏距离过程中，要求总体样本数大于样本的维数，否则得到的总体样本协方差矩阵逆矩阵不存在，这种情况下，用欧式距离来代替马氏距离，也可以理解为，如果样本数小于样本的维数，这种情况下求其中两个样本的距离，采用欧式距离计算即可。
3）还有一种情况，满足了条件总体样本数大于样本的维数，但是协方差矩阵的逆矩阵仍然不存在，比如A（3，4），B（5，6）；C（7，8），这种情况是因为这三个样本在其所处的二维空间平面内共线（如果是大于二维的话，比较复杂）。这种情况下，也采用欧式距离计算。
4）在实际应用中“总体样本数大于样本的维数”这个条件是很容易满足的，而所有样本点出现3）中所描述的情况是很少出现的，所以在绝大多数情况下，马氏距离是可以顺利计算的，但是马氏距离的计算是不稳定的，不稳定的来源是协方差矩阵，这也是马氏距离与欧式距离的最大差异之处。
综上，我们用python编写了马氏距离，如下：

distances=[]
for i in range(dataSetSize):
    x = numpy.array(dataSet)
    xt=x.T
    D=numpy.cov(xt)
    invD=numpy.linalg.inv(D)
    tp=inX-dataSet[i]
    distances.append(numpy.sqrt(dot(dot(tp,invD),tp.T)))

最后得到的distances就是测试样本和每个训练样本的马氏距离。

二、 wk_NNC算法

wk-NNC算法是对经典knn算法的改进，这种方法是对k个近邻的样本按照他们距离待分类样本的远近给一个权值w：

是第i个近邻的权值，其中1<i<k,是待测样本距离第i个近邻的距离。

用python实现这个算法比较简单：

def wk_knn(inX, dataSet, labels, k):
    dataSetSize = dataSet.shape[0]
    diffMat = tile(inX, (dataSetSize,1)) - dataSet  

    sqDiffMat = diffMat**2
    sqDistances = sqDiffMat.sum(axis=1) 
    distances = sqDistances**0.5
    sortedDistIndicies = distances.argsort()        
    classCount={}   
    w=[]     
    for i in range(k):
        w.append((distances[sortedDistIndicies[k-1]]-distances[sortedDistIndicies[i]]
        )/(distances[sortedDistIndicies[k-1]]-distances[sortedDistIndicies[0]]))
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel,0) + w[i]
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

 

三、 knnm算法

knnm算法运用了训练样本中的每一个模式，对训练样本的每个类，

1 ≤ i ≤ c，在每一个类中找出距离测试样本距离最近的k个近邻，假设这k个近邻的均值为，同样的，i从1到c变化，我们得到，如果是M当中距离测试样本最近的，则测试样本属于类。

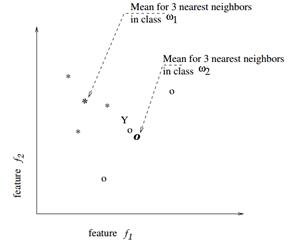
       如下图所示，对于一个两类的问题，每个类选三个近邻，类用*表示，类用o表示，“Y”是测试样本，则Y属于类。

用python实现如下：

def knnm(inX, dataSet, labels, k):
    dataSetSize = dataSet.shape[0]
    diffMat = tile(inX, (dataSetSize, 1)) - dataSet   #tile repeat inX to (dataSetSize,1)
    sqDiffMat = diffMat ** 2
    sqDistances = sqDiffMat.sum(axis=1)  #sum per row
    distances = sqDistances ** 0.5
    sortedDistIndicies = distances.argsort()
    classCount={}
    classNum={}
    i=0
    while i<dataSetSize:
        voteIlabel = labels[sortedDistIndicies[i]]
        if sum(classNum)==10*k:
            break
        elif classNum.get(voteIlabel,0)==k:
            i += 1
        else:
            classCount[voteIlabel] = classCount.get(voteIlabel,0)
                                     + distances[sortedDistIndicies[i]]
            classNum[voteIlabel]=classNum.get(voteIlabel,0)+1
            i += 1
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1))
    return sortedClassCount[0][0]

四、 实验过程

我在手写字符和约会数集分别作了实验，结果如下（k=7）：

约会数集错误率	KNN	WK_KNN	KNNM
马氏距离	6%	6.6%	6.2%
欧氏距离	5.8%	6.2%	6.2%

由于手写字符训练样本协方差矩阵不可逆，因此只能求欧氏距离

手写字符错误率	KNN	WK_KNN	KNNM
欧式距离	1.1628%(k=3最小)	0.9514%(k=5最小)	1.2685%(k=3最小)

五、实验小结

欧式距离比马氏距离计算量小得多，速度快，而且可以看出分类的效果甚至比马氏距离要好，,可以看到，在约会数集中，knn的表现要优于其他两种算法，欧式距离的knn错误率最低，而wk_knn在手写字符识别中有较为出色的表现，相对于其他两种算法，knnm并没有想象中的效果。