概念
树:是一种数据结构,它是由n(n>=1)个有限节点组成一个具有层次关系的集合。
二叉树:是一种特殊的树。
结点的度:结点拥有的子树个数
叶结点(叶):度为0的结点,即没有儿子的结点
分支结点:度不为0的结点
兄弟结点:具有相同父亲的结点
树的度:树中最大的结点度
结点的层次:根为第一层,依次类推
深度:树中节点的最大层次
高度:从下往上数层数
如果根结点第0,层数=深度=高度-1
如果根结点第1,层数=深度=高度
特点
1、每个结点最多有两颗子树,结点的度最大为2。
2、左子树和右子树是有顺序的,次序不能颠倒。
3、即使某结点只有一个子树,也要区分左右子树。
类型
满二叉树:顾名思义,布满结点的树,从高到低,除了叶节点外,每一个结点都有左右子叶,且叶子结点都处在最底层的二叉树。
完全二叉树:比满二叉树少几个叶节点,除最底层外,其它各层结点数都达到最大个数,底层的叶子结点都是从左到右依次排布。
平衡二叉树(AVL树):空树或者它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树也都是平衡树。
二叉搜索树:空树或者二叉树的所有节点比他的左子节点大,比他的右子节点小。(左<=根<=右)
红黑树:不仅是具有二叉搜索树的属性,还具有平衡树的属性,有序且子树差不超过1,颜色规则:结点要么红要么黑,上下层结点红黑交替,根节点和特殊节点(即叶节点下面两个虚无的节点)是黑的,红节点的左右子节点是黑的,最重要的是从任一节点到其每个叶子节点的所有路径都包含相同数目的黑色节点。
遍历方式
深度遍历:前中后序三种
前序遍历:根结点->左子树->右子树
中序遍历:左子树->根结点->右子树
后序遍历:左子树->根结点->根节点
广度遍历:
层次遍历:按层,从上到下,从左到右遍历。
扩展
红黑树插入结点问题
一般默认插入节点是红色的。
若插入以后树不符合颜色规则,则需要进行颜色调整。
若插入以后树已经不是一个平衡的二叉树,则需要进行结构调整。
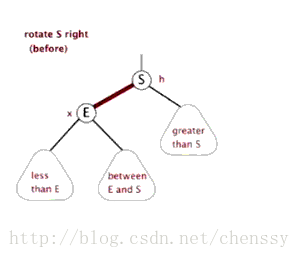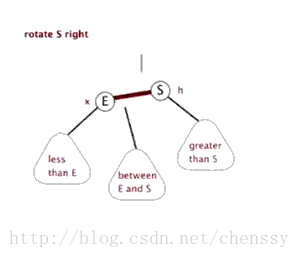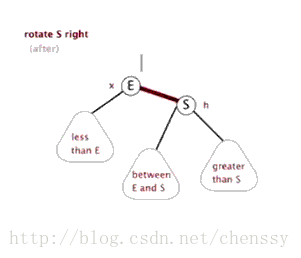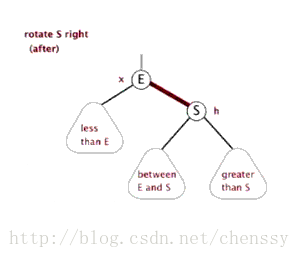
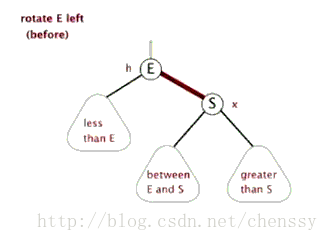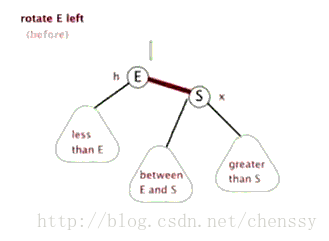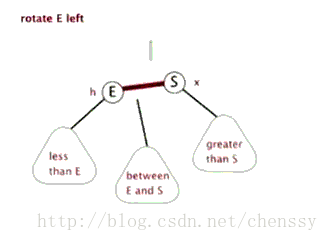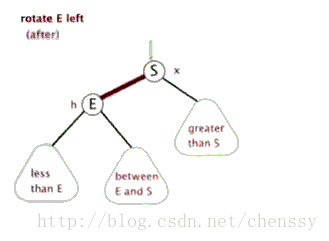
结构调整过程包含两个基本操作:左旋(Rotate Left),右旋(RotateRight)。
左旋
右旋