二维前缀和详解

我们讲一下什么是二维前缀和，建立在一维前缀和之上，我们要求一个矩阵内一个任意的子矩阵的数的和，我们就可以用二维前缀和，我们还是用DP来预处理，状态和一维前缀和差不多，只不过我们多加了一维，DP[i][j]表示（1,1）这个点与（i，j）这个点两个点分别为左上角和右下角所组成的矩阵内的数的和，好好想一下状态转移方程，DP[i][j]=DP[i-1][j]+DP[i][j-1]-DP[i-1][j-1]+map[i][j],怎么来的呢？我们画一下图就知道了。

这张图就知道了（i，j）可以由（i-1，j）和（i,j-1）两块构成，不过要注意两个点

1. 有一块矩阵我们重复加了，也就是（i-1，j-1）这一块，所以我们要减去它。

2. 我们这个矩阵是不完整的，由图可知我们还有一块深蓝色的没有加，也就是（i，j）这一点，所以我们要再加上map[i][j]也就是题目给出的矩阵中这一格的数。

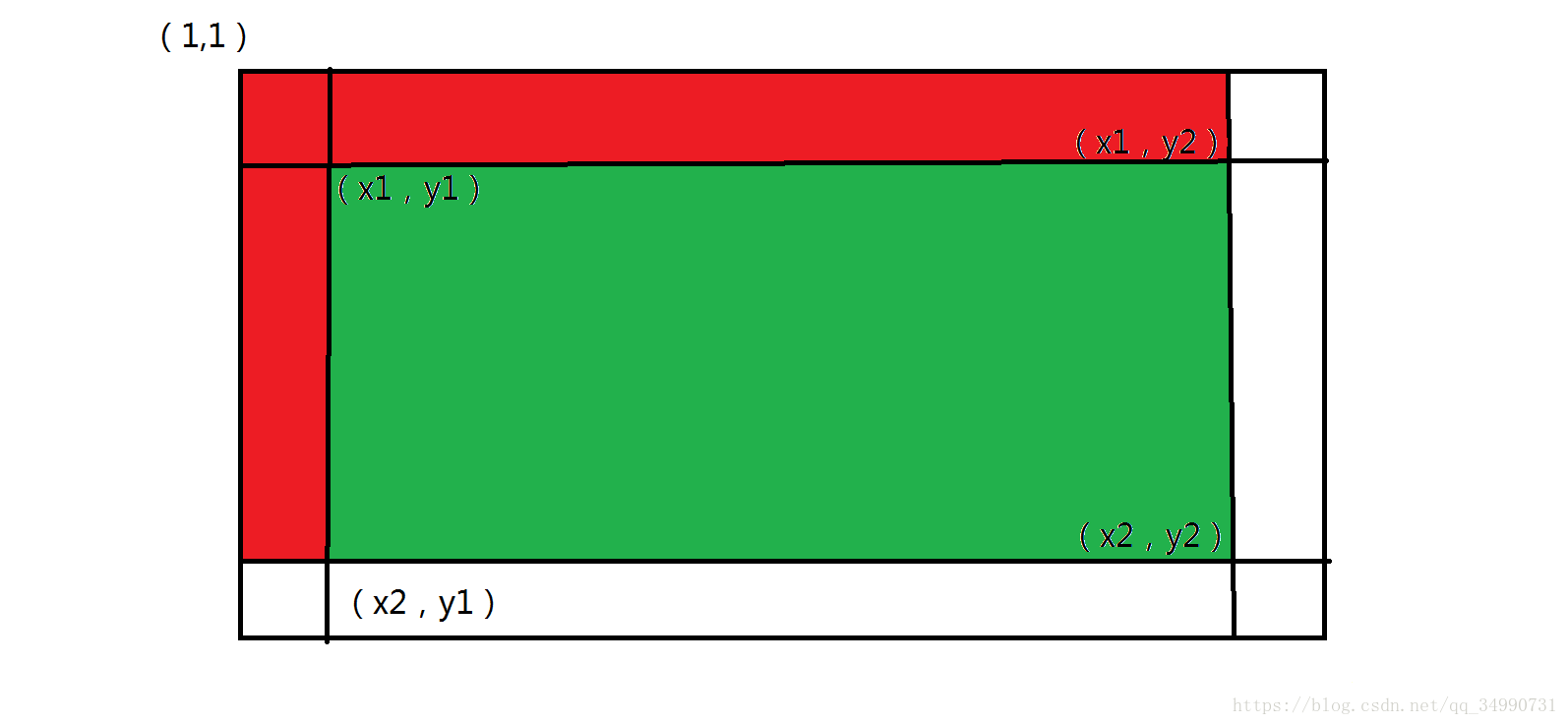
这样我们就预处理完了，现在讲一下怎么通过我们的预处理从而快速地得出我们想要的任意子矩阵中的和，我们定义（x1，y1）为我们想要子矩阵的左上角，（x2，y2）为我们想要子矩阵的右下角，然后我们画图想一想。

我们可以通过DP[x2][y2]来计算，我们通过图可以发现这个距离我们要的还差红色的部分看看怎么表示红色部分？我们可以分割成两块，分别是DP[x1][y2]和DP[x2][y1]我们发现有一块重复减了，所以我们再加上它即DP[x1][y1]。

有一点注意，因为画图和定义原因我们发现边界好像不对，我们来看看，我们定义的状态是整个矩阵包括边的和，而我们要求的也是要包括边的，所以我们要再改一下，把DP[x1][y2]和DP[x2][y1]和DP[x1][y1]分别改成DP[x1-1][y2]和DP[x2][y1-1]和DP[x1-1][y1-1]

这样一减我们就可以得到自己想要的答案，整理可得公式，DP[x2][y2]-DP[x1-1][y2]-DP[x2][y1-1]+DP[x1-1][y1-1]这样我们就可以做到O（1）之内查询，很奇妙吧，我们看一下实现代码：

#include<iostream>
#include<cstring>
using namespace std;
int dp[2000][2000],map[2000][2000];
int main()
{
	int m,n,k;//所给的矩阵是n*m的,有k组查询 
	cin >>n>>m>>k;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			cin >>map[i][j];
	memset(dp,0,sizeof(dp));
	for(int i=1;i<=n;i++)//预处理一波 
		for(int j=1;j<=m;j++)
			dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+map[i][j];
	for(int i=1;i<=k;i++)//接受查询 
	{
		int x1,x2,y1,y2;
		cin >>x1>>y1>>x2>>y2;
		cout <<(dp[x2][y2]+dp[x1-1][y1-1]-dp[x1-1][y2]-dp[x2][y1-1])<<endl;//O（1）查询 
	}
	return 0;
}

参考博文:https://blog.csdn.net/qq_34990731/article/details/82807870