三分钟带你快速实现二叉树的递归遍历

写在前面：

上一篇文章中我们聊到了队列——漫画趣解——队列
相信很多小伙伴都知道了如何实现队列；
那么这次，时光同样采用漫画形式，
给大家聊一聊什么是二叉树，如何实现二叉树的递归遍历；

思维导图：

​

什么是树？

​

树是一种非线性结构，有一个直接前驱，但可能有多个直接后继（1：n）；
树的定义具有递归性，树中还有树；
树可以为空，即结节点个数为0；

如图：

​

若干术语：

根：根节点，没有前驱；
叶子：终端结点，没有后继；
双亲：上层的那个结点，就是直接前驱；
孩子：下层结点的子树，就是直接后继；
结点：树的数据元素；（上图的结点数为11）
结点的度：结点挂接的子树数，有几个直接后继就是几度；
树的度：所有结点度中的最大值，Max{各结点的度}，（上图树的度为2）；
树的深度（或高度）：所有结点中最大的层数，（上图数的深度为3层）；

什么是二叉树？

​

二叉树：
​

特征：每个结点最多只有两个子结点（不存在度大于2的结点）；

​

5种形态：
​

常见的二叉树有两种重要形态，满二叉树和完全二叉树；

满二叉树：
叶子结点全部都在最底层；
除叶子结点外，每个结点都有左右两个子节点；

​

完全二叉树：
叶子结点全都都在最底的两层；
最后一层只缺少右边的叶子结点，左边一定有叶子结点；
除了最后一层，其它层的结点个数均达到最大值；

​

二叉树的遍历：

二叉树也是有顺序存储和链式存储，那么其中存储的数据如何读取出来呢？

​

于是就有了二叉树的遍历，总共有3种遍历方式：
先序遍历，中序遍历和后序遍历；
先序遍历：

也就是先访问根结点，再左边子结点，最后右边子结点；俗称DLR；

上图中先序遍历访问的结果就是：

A-B-C-D-E-F-G-H；

中序遍历：

也就是先访问左结点，再根结点，最后右结点；俗称LDR；

上图中中序遍历访问的结果是：

B-D-C-E-A-F-H-G;

后序遍历：

先访问左结点，再右结点，最后根结点；俗称LRD；

上图中后序遍历访问的结果是：

D-E-C-B-H-G-F-A；

​

代码实现：

文中完整源码获取请关注公众号《程序员的时光》；
后台回复——数据结构源码，可以获得常见数据结构代码；

二叉树递归遍历实现；
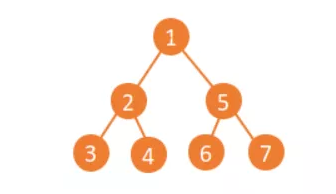
我们以这个二叉树为例：

​

结点实体类：

 1package com.java.model;
 2
 3public class BinaryTreeNode {
 4    //树的根结点
 5    public char ch;
 6    //左结点
 7    public BinaryTreeNode lchild;
 8    //右结点
 9    public BinaryTreeNode rchild;
10
11    //构造函数
12    public BinaryTreeNode(char ch, BinaryTreeNode lchild, BinaryTreeNode rchild) {
13        this.ch = ch;
14        this.lchild = lchild;
15        this.rchild = rchild;
16    }
17}

方法类：

 1package com.java.dao;
 2
 3import com.java.model.BinaryTreeNode;
 4
 5//二叉树递归遍历
 6public class BTRecursionDao {
 7    public void RecursionBiTree(BinaryTreeNode root){
 8        if(root==null){
 9            return;
10        }
11        //先序遍历
12        System.out.print(root.ch+" ");
13        RecursionBiTree(root.lchild);
14        RecursionBiTree(root.rchild);
15
16        /**
17         * 中序遍历(其实就是把顺序调换一下)
18         * RecursionBiTree(root.lchild);
19         * System.out.print(root.ch+" ");
20         * RecursionBiTree(root.rchild);
21         */
22
23        /**
24         * 后序遍历
25         * RecursionBiTree(root.lchild);
26         * RecursionBiTree(root.rchild);
27         * System.out.print(root.ch+" ");
28         */
29    }
30}

主函数：

1package com.java.main;
 2
 3import com.java.dao.BTRecursionDao;
 4import com.java.model.BinaryTreeNode;
 5
 6public class BTRecursionMain {
 7    public static void main(String[] args) {
 8        BTRecursionDao btRecursionDao=new BTRecursionDao();
 9        //创建树结点
10        BinaryTreeNode node1=new BinaryTreeNode('A',null,null);
11        BinaryTreeNode node2=new BinaryTreeNode('B',null,null);
12        BinaryTreeNode node3=new BinaryTreeNode('C',null,null);
13        BinaryTreeNode node4=new BinaryTreeNode('D',null,null);
14        BinaryTreeNode node5=new BinaryTreeNode('E',null,null);
15        BinaryTreeNode node6=new BinaryTreeNode('F',null,null);
16        BinaryTreeNode node7=new BinaryTreeNode('G',null,null);
17        BinaryTreeNode node8=new BinaryTreeNode('H',null,null);
18
19        //建立结点间的关系
20        node1.lchild=node2;  /* node1就是A，结点A的左孩子是B(node2)，右孩子是F(node6) */
21        node1.rchild=node6;
22        node2.rchild=node3;  /* node2就是B，结点B的左孩子为null(初始化就是null，所以不用管)，右孩子是C(node3) */
23        node3.lchild=node4;
24        node3.rchild=node5;
25        node6.rchild=node7;
26        node7.lchild=node8;
27
28        //递归遍历
29        System.out.println("先序遍历结果:");
30        btRecursionDao.RecursionBiTree(node1);  /* 根结点为A */
31    }
32}

运行结果（这里以先序遍历为例）：

​

读者可以自行试试中序遍历和后序遍历；

好了，今天就先分享到这里了，下期给大家带来二叉树的非递归遍历的讲解！
更多采用漫画趣解编程知识的文章，欢迎关注我的微信公众号，一起学习进步！

​

                                        原创实属不易，求个关注吧~