【NOIP模拟赛】皇后游戏

【引子】
还记得 NOIP 2012 提高组 Day1 的国王游戏吗？时光飞逝，光阴荏苒，两年过去了。国王游戏早已过时，如今已被皇后游戏取代，请你来解决类似于国王游戏的另一个问题。
【问题描述】
皇后有 n 位大臣，每位大臣的左右手上面分别写上了一个正整数。恰逢国庆节来临，皇后决定为 n 位大臣颁发奖金，其中第 i 位大臣所获得的奖金数目为第i－1 位大臣所获得奖金数目与前 i 位大臣左手上的数的和的较大值再加上第 i 位
大臣右手上的数。
形式化地讲： 我们设第 i 位大臣左手上的正整数为 ai， 右手上的正整数为 bi，则第 i 位大臣获得的奖金数目为 ci 可以表达为：

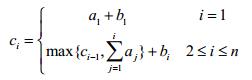
当然，吝啬的皇后并不希望太多的奖金被发给大臣，所以她想请你来重新安排一下队伍的顺序，使得获得奖金最多的大臣，所获奖金数目尽可能的少。
注意：重新安排队伍并不意味着一定要打乱顺序，我们允许不改变任何一位大臣的位置。
【输入格式】
第一行包含一个正整数 T，表示测试数据的组数。
接下来 T 个部分，每个部分的第一行包含一个正整数 n，表示大臣的数目。
每个部分接下来 n 行中，每行两个正整数，分别为 ai 和 bi， 含义如上文所述。
【输出格式】
共 T 行，每行包含一个整数，表示获得奖金最多的大臣所获得的奖金数目。
【样例输入 1】
1
3
4 1
2 2
1 2

【样例输出 1】
8
【样例说明 1】
按照 1、2、3 这样排列队伍，获得最多奖金的大臣获得奖金的数目为 10；
按照 1、3、2 这样排列队伍，获得最多奖金的大臣获得奖金的数目为 9；
按照 2、1、3 这样排列队伍，获得最多奖金的大臣获得奖金的数目为 9；
按照 2、3、1 这样排列队伍，获得最多奖金的大臣获得奖金的数目为 8；
按照 3、1、2 这样排列队伍，获得最多奖金的大臣获得奖金的数目为 9；
按照 3、2、1 这样排列队伍，获得最多奖金的大臣获得奖金的数目为 8。
当按照 3、2、1 这样排列队伍时，三位大臣左右手的数分别为：
(1, 2)、(2, 2)、(4, 1)
第 1 位大臣获得的奖金为 1 + 2 = 3；
第 2 位大臣获得的奖金为 max{3, 3} + 2 = 5；
第 3 为大臣获得的奖金为 max{5, 7} + 1 = 8。
【样例输入 2】
2
5
85 100
95 99
76 87
60 97
79 85
12
9 68
18 45
52 61
39 83
63 67
45 99
52 54
82 100
23 54
99 94
63 100
52 68
【样例输出 2】
528
902

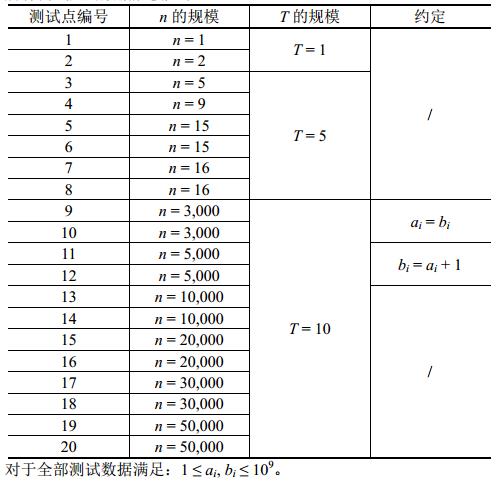
【数据规模与约定】
所有测试点的数据规模如下：

【特别提示】
由于评测在 Linux 下进行，请 C++选手务必注意 Linux 系统下 rand()函数返
回值的取值范围是[0, 2^31)。

分析

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn=200000+5;
inline int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1; ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}
int n,t;
ll f[maxn];
struct node
{
    int a,b;
    bool operator < (const node &j) const {
        return min(a,j.b)<min(b,j.a);
    }
}p[maxn];
int main()
{
    freopen("game.in","r",stdin);
    freopen("game.out","w",stdout);
    int testcase=read();
    while(testcase--)
    {
        n=read();
        for(int i=1;i<=n;i++)
        {p[i].a=read(); p[i].b=read();}
        sort(p+1,p+n+1);
        ll s=0;
        for(int i=1;i<=n;i++)
        {
            s+=p[i].a;
            f[i]=max(f[i-1],s)+p[i].b;
        }
        printf("%lld
",f[n]);
    }
    fclose(stdin); fclose(stdout);
    return 0;
}