【引子】
还记得 NOIP 2012 提高组 Day2 中的借教室吗?时光飞逝,光阴荏苒,两年过去了,曾经借教室的同学们纷纷归还自己当初租借的教室。请你来解决类似于借教室的另一个问题。
【问题描述】
在接受借教室请求的 n 天中,第 i 天剩余的教室为 ai 个。作为大学借教室服务的负责人,你需要完成如下三种操作共 m 次:
① 第 l 天到第 r 天,每天被归还 d 个教室。
② 询问第 l 天到第 r 天教室个数的平均数。
③ 询问第 l 天到第 r 天教室个数的方差。
【输入格式】
第一行包括两个正整数 n 和 m,其中 n 为借教室的天数,m 为操作次数。
接下来一行,共包含 n 个整数,第 i 个整数表示第 i 天剩余教室数目为 ai 个。
接下来 m 行,每行的第一个整数为操作编号(只能为 1 或 2 或 3) ,接下来包含两个正整数 l 和 r,若操作编号为 1,则接下来再包含一个正整数 d。
【输出格式】
对于每个操作 2 和操作 3,输出一个既约分数(分子与分母互质)表示询问的答案(详见样例)。若答案为 0,请输出“0/1” (不含引号)。
【样例输入】
5 4
1 2 3 4 5
1 1 2 3
2 2 4
3 2 4
3 1 5
【样例输出】
4/1
2/3
14/25
【样例说明】

【数学小贴士】
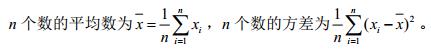
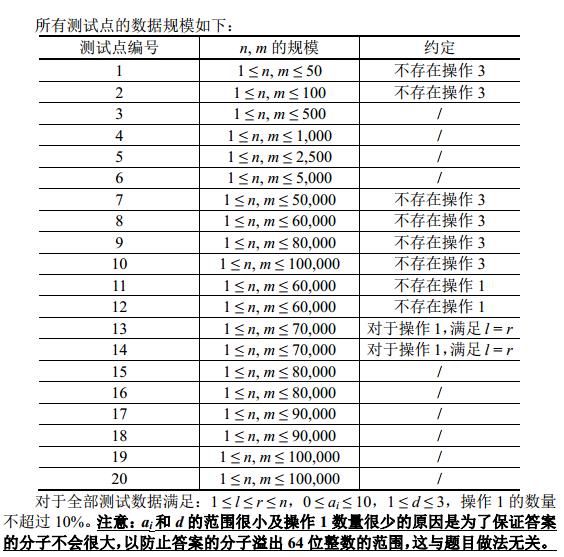
【数据规模与约定】
分析
区间修改和区间查询,很明显这是一道线段树的题。关于平均数的求法,只要记录区间和就行了,麻烦一点的就是方差。
为了方便举例子,例如求两个数x1,x2的方差,设t是t=(x1+x2)/2; 那么方差p=((x1-t)^2+(x2-t)^2)/2; 展开得到
p=((x1^2+x2^2)-2(x1+x2)*t+2*t^2)/2; 可以发现只需要这个区间的平方和和区间和就可以求出方差(平均数可以用区间和求得),之后用线段树维护就行了。
还有一点是要注意要防止过程量溢出。
代码
代码虽然很长(线段树的代码貌似都不短),但是思路清晰地话代码的长的不是问题。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int maxn=100000+5; typedef long long ll; inline int read() { int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-') f=-1; ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();} return x*f; } int n,m,len; int a[maxn]; struct node { int l,r,lc,rc; ll c,mul,add; }tr[maxn<<1]; void bt(int x,int y) { len++; int now=len; tr[now].l=x; tr[now].r=y; tr[now].lc=tr[now].rc=0; if(x==y) { tr[now].c=a[x]; tr[now].mul=a[x]*a[x]; } else { int mid=(x+y)>>1; tr[now].lc=len+1; bt(x,mid); tr[now].rc=len+1; bt(mid+1,y); tr[now].c=tr[tr[now].lc].c+tr[tr[now].rc].c; tr[now].mul=tr[tr[now].lc].mul+tr[tr[now].rc].mul; } } inline void pushdown(int now) { if(tr[now].l==tr[now].r||!tr[now].add) return; int lc=tr[now].lc,rc=tr[now].rc; tr[lc].mul=tr[lc].mul+2*tr[lc].c*tr[now].add+(tr[lc].r-tr[lc].l+1)*tr[now].add*tr[now].add; tr[rc].mul=tr[rc].mul+2*tr[rc].c*tr[now].add+(tr[rc].r-tr[rc].l+1)*tr[now].add*tr[now].add; tr[lc].c=tr[lc].c+(tr[lc].r-tr[lc].l+1)*tr[now].add; tr[rc].c=tr[rc].c+(tr[rc].r-tr[rc].l+1)*tr[now].add; tr[lc].add+=tr[now].add; tr[rc].add+=tr[now].add; tr[now].add=0; } void update(int now,int x,int y,int d) { if(tr[now].l==x&&tr[now].r==y) { tr[now].mul=tr[now].mul+2*tr[now].c*d+(tr[now].r-tr[now].l+1)*d*d; tr[now].c=tr[now].c+(y-x+1)*d; tr[now].add+=d; }else { pushdown(now); int lc=tr[now].lc,rc=tr[now].rc; int mid=(tr[now].l+tr[now].r)>>1; if(y<=mid) update(lc,x,y,d); else if(x>=mid+1) update(rc,x,y,d); else { update(lc,x,mid,d); update(rc,mid+1,y,d); } tr[now].c=tr[lc].c+tr[rc].c; tr[now].mul=tr[lc].mul+tr[rc].mul; } } ll getsum(int now,int x,int y) { if(tr[now].l==x&&tr[now].r==y) return tr[now].c; else { pushdown(now); int lc=tr[now].lc,rc=tr[now].rc; int mid=(tr[now].l+tr[now].r)>>1; if(y<=mid) return getsum(lc,x,y); else if(x>=mid+1) return getsum(rc,x,y); else return getsum(lc,x,mid)+getsum(rc,mid+1,y); } } ll getmul(int now,int x,int y) { if(tr[now].l==x&&tr[now].r==y) return tr[now].mul; else { pushdown(now); int lc=tr[now].lc,rc=tr[now].rc; int mid=(tr[now].l+tr[now].r)>>1; if(y<=mid) return getmul(lc,x,y); else if(x>=mid+1) return getmul(rc,x,y); else return getmul(lc,x,mid)+getmul(rc,mid+1,y); } } ll gcd(ll a, ll b) { if(b==0) return a; return gcd(b,a%b); } int main() { freopen("classroom.in","r",stdin); freopen("classroom.out","w",stdout); n=read();m=read(); for(int i=1;i<=n;i++) a[i]=read(); bt(1,n); for(int i=1;i<=m;i++) { int p,x,y,d; p=read(); if(p==1) { x=read(); y=read(); d=read(); update(1,x,y,d); }else { x=read(); y=read(); ll sum,num,fz,fm,t; sum=getsum(1,x,y); num=y-x+1; if(!sum){printf("%d/%d ",0,1); continue;} t=gcd(sum,num); if(p==2) printf("%lld/%lld ",sum/t,num/t); else if(p==3) { ll mul=getmul(1,x,y); fz=mul*num-sum*sum; fm=num*num; t=gcd(fz,fm); printf("%lld/%lld ",fz/t,fm/t); } } } fclose(stdin); fclose(stdout); return 0; }