P3415 祭坛
题目背景
在遥远的Dgeak大陆,生活着一种叫做Dar-dzo-nye的怪物。每当这种怪物降临,人们必须整夜对抗怪物而不能安睡。为了乞求这种怪物不再降临,人们决定建造祭坛。
题目描述
Dgeak大陆可以看成一个用平面直角坐标系表示的巨大平面。在这个平面上,有 n 个Swaryea水晶柱,每个水晶柱可以用一个点表示。
如果 4 个水晶柱依次相连可以构成一个四边形,满足其两条对角线分别平行于 x 轴和 y 轴,并且对角线的交点位于四边形内部(不包括边界),那么这 4 个水晶柱就可以建立一个结界。其中,对角线的交点称作这个结界的中心。
例如下左图中,水晶柱 ABCD 可以建立一个结界,其中心为 O。
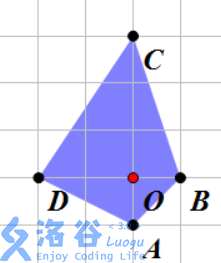
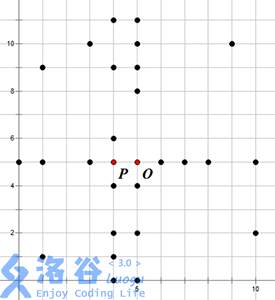
为了起到抵御Dar-dzo-nye的最佳效果,人们会把祭坛修建在最多层结界的保护中。其中不同层的结界必须有共同的中心,这些结界的边界不能有任何公共点,并且中心处也不能有水晶柱。这里共同中心的结界数量叫做结界的层数。
为了达成这个目的,人们要先利用现有的水晶柱建立若干个结界,然后在某些结界的中心建立祭坛。
例如上右图中,黑色的点表示水晶柱(注意 P 和 O 点不是水晶柱)。祭坛的一个最佳位置为 O 点,可以建立在 3 层结界中,其结界的具体方案见下左图。当然,建立祭坛的最佳位置不一定是唯一,在上右图中,O 点左侧 1 单位的点 P 也可以建立一个在 3 层结界中的祭坛,见下右图。
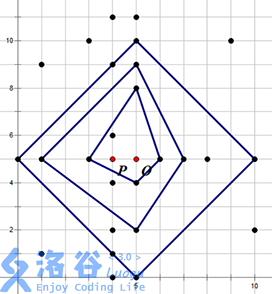
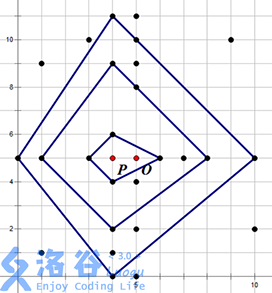
现在人们想知道:
祭坛最佳选址地点所在的结界层数;
祭坛最佳的选址地点共有多少个。
输入输出格式
输入格式:
输入的第一行包含两个正整数 n,表示水晶柱的个数
接下来 n 行,每行包含两个非负整数 x,y,表示每个水晶柱的坐标。保证相同的坐标不会重复出现。
输出格式:
第一行一个整数,表示祭坛最多可以位于多少个结界的中心
第二行一个整数,表示结界数最多的方案有多少种。
输入输出样例
输入样例#1:
26
0 5
1 1
1 5
1 9
3 5
3 10
4 0
4 1
4 2
4 4
4 6
4 9
4 11
5 0
5 2
5 4
5 8
5 9
5 10
5 11
6 5
7 5
8 5
9 10
10 2
10 5
输出样例#1:
3
2
说明
对于(30\%)的数据 (n leq 1000)
另外(30\%)的数据 (n leq 10000)
剩下的(40\%)数据 (n leq 100000)
保证 (0 leq x, y leq n)
题解
二分答案 + 扫描线。
二分答案mid。一个点满足条件当且仅当这个点上下左右四个方向上点数最小值(geq mid)
在x上扫,维护线左边、右边的点数,对于扫描线上的点,不难确定其在上下方向上满足条件的点的区间,只需要判断在左右方向上满足的点的个数即可。
可以在维护上下点数的同时,判断是否上下点数同时(geq mid),若是则标记坐标为1,区间和即为在左右方向上满足的点的个数。
单点修改,区间查询。BIT即可。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <map>
#include <string>
#include <cmath>
#include <sstream>
inline int lowbit(int x){return x & -x;}
inline void read(int &x)
{
x = 0;char ch = getchar(), c = ch;
while(ch < '0' || ch > '9') c = ch, ch = getchar();
while(ch <= '9' && ch >= '0') x = x * 10 + ch - '0', ch = getchar();
if(c == '-') x = -x;
}
const int INF = 0x3f3f3f3f;
const int MAXN = 100000 + 10;
int n, up[MAXN], down[MAXN], q[MAXN], tot;
std::vector<int> vec[MAXN];
int data[MAXN], shu[MAXN];
void modify(int p, int k)
{
++ p;
for(;p <= n + 1;p += lowbit(p)) data[p] += k;
}
int ask(int p)
{
++ p;
int sum = 0;
for(;p;p -= lowbit(p)) sum += data[p];
return sum;
}
int check(int mid)
{
int num = 0;
memset(shu, 0, sizeof(shu)), memset(data, 0, sizeof(data));
memset(down, 0, sizeof(down)), memset(up, 0, sizeof(up));
for(int i = 1;i <= tot;++ i)
for(int j = vec[q[i]].size() - 1;j >= 0;-- j)
++ down[vec[q[i]][j]];
for(int k = 1;k <= tot;++ k)
{
int i = q[k];
for(int j = vec[i].size() - 1;j >= 0;-- j)
{
-- down[vec[i][j]];
if((down[vec[i][j]] < mid || up[vec[i][j]] < mid) && shu[vec[i][j]])
shu[vec[i][j]] = 0, modify(vec[i][j], -1);
}
if(mid - 1 < vec[i].size())
{
int l = vec[i][mid - 1], r = vec[i].size() - mid;
if(r >= 0)
{
r = vec[i][r];
if(r > 0 && l <= r - 1) num += ask(r - 1) - ask(l);
}
}
for(int j = vec[i].size() - 1;j >= 0;-- j)
{
++ up[vec[i][j]];
if(down[vec[i][j]] >= mid && up[vec[i][j]] >= mid && !shu[vec[i][j]])
shu[vec[i][j]] = 1, modify(vec[i][j], 1);
}
}
return num;
}
int main()
{
read(n);
for(int i = 1;i <= n;++ i)
{
int x,y;read(x), read(y);
vec[x].push_back(y);
q[++ tot] = x;
}
std::sort(q + 1, q + 1 + tot);
tot = std::unique(q + 1, q + 1 + tot) - q - 1;
for(int i = 1;i <= tot;++ i) std::sort(vec[q[i]].begin(), vec[q[i]].end());
int l = 1, r = n, ans = 0, num = 0;
while(l <= r)
{
int mid = l + r >> 1, tmp;
if(tmp = check(mid)) ans = mid, l = mid + 1, num = tmp;
else r = mid - 1;
}
printf("%d
%d", ans, num);
return 0;
}