Wherever the destination is, whoever we meet, let's render this song together.
On a Cartesian coordinate plane lies a rectangular stage of size w × h, represented by a rectangle with corners (0, 0), (w, 0), (w, h) and (0, h). It can be seen that no collisions will happen before one enters the stage.
On the sides of the stage stand n dancers. The i-th of them falls into one of the following groups:
- Vertical: stands at (xi, 0), moves in positive y direction (upwards);
- Horizontal: stands at (0, yi), moves in positive x direction (rightwards).
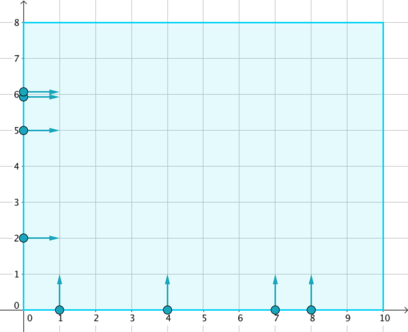
According to choreography, the i-th dancer should stand still for the first ti milliseconds, and then start moving in the specified direction at 1 unit per millisecond, until another border is reached. It is guaranteed that no two dancers have the same group, position and waiting time at the same time.
When two dancers collide (i.e. are on the same point at some time when both of them are moving), they immediately exchange their moving directions and go on.
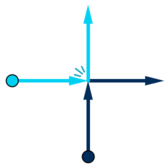
Dancers stop when a border of the stage is reached. Find out every dancer's stopping position.
The first line of input contains three space-separated positive integers n, w and h (1 ≤ n ≤ 100 000, 2 ≤ w, h ≤ 100 000) — the number of dancers and the width and height of the stage, respectively.
The following n lines each describes a dancer: the i-th among them contains three space-separated integers gi, pi, and ti (1 ≤ gi ≤ 2, 1 ≤ pi ≤ 99 999, 0 ≤ ti ≤ 100 000), describing a dancer's group gi (gi = 1 — vertical, gi = 2 — horizontal), position, and waiting time. If gi = 1 then pi = xi; otherwise pi = yi. It's guaranteed that 1 ≤ xi ≤ w - 1 and 1 ≤ yi ≤ h - 1. It is guaranteed that no two dancers have the same group, position and waiting time at the same time.
Output n lines, the i-th of which contains two space-separated integers (xi, yi) — the stopping position of the i-th dancer in the input.
8 10 8
1 1 10
1 4 13
1 7 1
1 8 2
2 2 0
2 5 14
2 6 0
2 6 1
4 8
10 5
8 8
10 6
10 2
1 8
7 8
10 6
3 2 3
1 1 2
2 1 1
1 1 5
1 3
2 1
1 3
The first example corresponds to the initial setup in the legend, and the tracks of dancers are marked with different colours in the following figure.
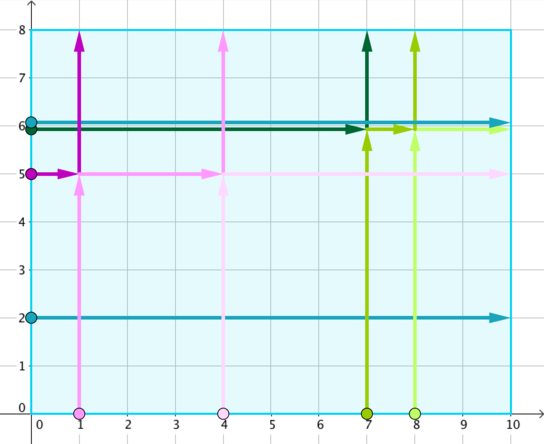
In the second example, no dancers collide.
【题解】
不(题)难(解)发(上)现(说)两个点能够相碰当且仅当p - t相等
于是我们可以按照p - t分组,发现两个点相碰可以看做穿过去。那么
最终位置与原始位置有什么对应关系呢?
我们把每个点的路径化成直线,交点意味着碰撞。我们发现一个点的行走轨迹是
阶梯状的,手画一下不难发现:左上->左下->右下方向的点对应左上->右上->
右下的点
于是两次间接排序即可

1 #include <iostream> 2 #include <cstdio> 3 #include <cstdlib> 4 #include <cstring> 5 #include <algorithm> 6 #define max(a, b) ((a) > (b) ? (a) : (b)) 7 #define min(a, b) ((a) < (b) ? (a) : (b)) 8 9 const int INF = 0x3f3f3f3f; 10 const int MAXN = 1000000 + 10; 11 12 inline void read(int &x) 13 { 14 x = 0;char ch = getchar(), c = ch; 15 while(ch < '0' || ch > '9')c = ch, ch = getchar(); 16 while(ch <= '9' && ch >= '0')x = x * 10 + ch - '0', ch = getchar(); 17 if(c == '-')x = -x; 18 } 19 20 inline int abs(int a) 21 { 22 return a < 0 ? -1*a : a; 23 } 24 25 struct Node 26 { 27 int g, p, t, x, y; 28 }node[MAXN],ans[MAXN]; 29 30 int n,w,h,cnt[MAXN],cnt2[MAXN]; 31 32 int cmp(int c, int d) 33 { 34 Node a = node[c], b = node[d]; 35 return (a.p - a.t == b.p - b.t) ? ( (a.y == b.y) ? (a.x > b.x) : (a.y < b.y)) : (a.p - a.t < b.p - b.t); 36 } 37 38 int cmp2(int c, int d) 39 { 40 Node a = node[c], b = node[d]; 41 return (a.p - a.t == b.p - b.t) ? ((a.x == b.x) ? (a.y < b.y) : (a.x > b.x)) : (a.p - a.t < b.p - b.t); 42 } 43 44 int main() 45 { 46 read(n), read(w), read(h); 47 for(register int i = 1;i <= n;++ i) 48 { 49 read(node[i].g), read(node[i].p), read(node[i].t); 50 if(node[i].g == 1) node[i].y = -1, node[i].x = node[i].p; 51 else node[i].y = node[i].p, node[i].x = -1; 52 cnt[i] = cnt2[i] = i; 53 } 54 std::sort(cnt + 1, cnt + 1 + n, cmp); 55 for(register int i = 1;i <= n;++ i) 56 if(node[i].x != -1)node[i].y = h; 57 else node[i].x = w; 58 std::sort(cnt2 + 1, cnt2 + 1 + n, cmp2); 59 for(register int i = 1;i <= n;++ i) 60 ans[cnt[i]] = node[cnt2[i]]; 61 for(register int i = 1;i <= n;++ i) 62 printf("%d %d ", ans[i].x, ans[i].y); 63 return 0; 64 }
