Radar Installation
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 89661 | Accepted: 20143 |
Description
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
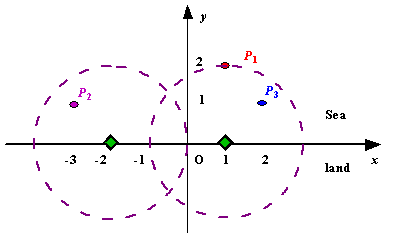
Figure A Sample Input of Radar Installations
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.

Figure A Sample Input of Radar Installations
Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 2 1 2 -3 1 2 1 1 2 0 2 0 0
Sample Output
Case 1: 2 Case 2: 1
Source
【题解】
每个点对应一段放置的区间,于是问题转化成了区间点覆盖问题。贪心即可

1 #include <iostream> 2 #include <iostream> 3 #include <cstdio> 4 #include <cstdlib> 5 #include <string> 6 #include <algorithm> 7 #include <cmath> 8 #define min(a, b) ((a) < (b) ? (a) : (b)) 9 10 const int INF = 0x7fffffff; 11 const int MAXN = 1000 + 10; 12 13 inline void read(int &x) 14 { 15 x = 0;char ch = getchar(),c = ch; 16 while(ch < '0' || ch > '9')c = ch, ch = getchar(); 17 while(ch <= '9' && ch >= '0')x = x * 10 + ch - '0', ch = getchar(); 18 if(c == '-')x = -x; 19 } 20 21 int n, R, cnt[MAXN], ans, t, ok; 22 double l[MAXN], r[MAXN], now; 23 24 bool cmp(int a, int b) 25 { 26 return l[a] < l[b]; 27 } 28 29 int main() 30 { 31 while(scanf("%d%d", &n, &R) && (n + R)) 32 { 33 ans = now = ok = 0; 34 register int x,y; 35 for(register int i = 1;i <= n;++i) 36 { 37 cnt[i] = i; 38 read(x);read(y); 39 if(R < y) ans = -1,ok = 1; 40 double tmp = sqrt(R * R - y * y); 41 l[i] = x - tmp; 42 r[i] = x + tmp; 43 } 44 if(ok)goto L1; 45 std::sort(cnt + 1, cnt + 1 + n, cmp); 46 now = -INF; 47 for(register int i = 1;i <= n;++ i) 48 if(l[cnt[i]] > now) ans ++, now = r[cnt[i]]; 49 else now = min(now, r[cnt[i]]); 50 L1: ; 51 if(!ans) ans = -1; 52 printf("Case %d: %d ", ++t, ans); 53 } 54 return 0; 55 }
