P1244 青蛙过河
题目描述
有一条河,左边一个石墩(A区)上有编号为1,2,3,4,…,n的n只青蛙,河中有k个荷叶(C区),还有h个石墩(D区),右边有一个石墩(B区),如下图所示。n只青蛙要过河(从左岸石墩A到右岸石墩B),规则为:
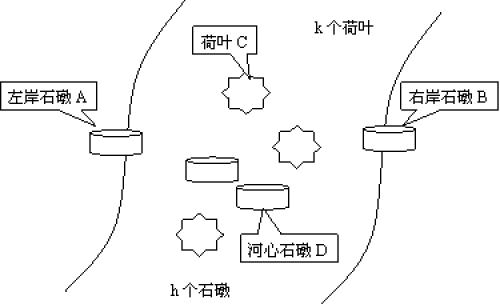
(1)石墩上可以承受任意多只青蛙,荷叶只能承受一只青蛙(不论大小);
(2)青蛙可以:A→B(表示可以从A跳到B,下同),A→C,A→D,C→B,D→B,D→C,C→D;
(3)当一个石墩上有多只青蛙时,则上面的青蛙只能跳到比它大1号的青蛙上面。
你的任务是对于给出的h,k,计算并输出最多能有多少只青蛙可以根据以上规则顺利过河?
输入输出格式
输入格式:两个整数h,k
输出格式:一个整数,表示最多能有多少只青蛙可以根据以上规则顺利过河。
输入输出样例
输入样例#1:
2 3
输出样例#1:
16
这里表面上是个dp,实际上体现了一个分治的思想。
定义状态:f[i][j]表示i个石墩j个荷叶最大青蛙数。
易知:f[0][k] = k + 1;(k只青蛙跳到C上,此时石墩A还剩下编号为k的青蛙,让它跳到石墩B作为底部,其他青蛙依次罗上去,符合要求)
那么对于f[1][k],最优情况是让 石墩D1被占满(f[0][k],此时当做没有石墩B,可以把石墩D1当做石墩B),并让青蛙把石墩B占满(f[0][k+1],此时当做没有石墩D1),因此f[1][k] = f[0][k] * 2 = 2^1 * (k + 1) = (2 << 1) * (k + 1)
对于f[2][k],最优情况是让 石墩D2被占满(f[1][k],此时当做没有石墩B,可以把石墩D2当做石墩B),并让青蛙把石墩D1占满(f[0][k],此时当做没有石墩B,可以把石墩D1当做石墩B),并让青蛙把
石墩B占满(f[0][k+1],此时当做没有石墩D1),因此f[2][k] = f[1][k] + f[0][k] * 2 = 2^2 * (k + 1) = (1 << 2) * (k + 1)
(括号中的内容体现了分治的思想)
以此类推:
f[3][k] = f[2][k] + f[1][k] + f[0][k] * 2 = (2^3) * (k + 1)
f[4][k] = f[3][k] + f[2][k] + f[1][k] + f[0][k] * 2 = (2^4) * (k + 1)
.
.
.
.
.
.
f[h][k] = (2 ^ h) * (k + 1)
所以。。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cstring>
#include <vector>
#define max(a,b) ((a) > (b) ? (a) : (b))
#define min(a,b) ((a) < (b) ? (a) : (b))
inline int read()
{
int x = 0;char ch = getchar();char c = ch;
while(ch > '9' || ch < '0')c = ch,ch = getchar();
while(ch <= '9' && ch >= '0')x = x * 10 + ch - '0',ch = getchar();
if(c == '-')return -1 * x;
return x;
}
const int INF = 99999999999;
int c,d;
int main()
{
d = read();c = read();
printf("%d", (1 << d) * (c + 1));
return 0;
}