一、 最小二乘法的由来
1805年,法国数学家Legendre发表了最小二乘法的第一个清晰简洁的论述;
1809年,德国数学家高斯发表了《天体运动论》,并声称自1795年以来就使用了最小二乘法。导致了与Legendre的优先权争议。
1829年,高斯提供了最小二乘法的优化效果强于其他方法的证明(高斯-马尔可夫定理)
二、参数估计——最小二乘法(正规方程)
1. 一元线性回归
对于一元线性回归模型 ![]() ,其中 ei 表示误差,可得
,其中 ei 表示误差,可得 ![]()
假设从总体中获取了n组观察值(X1,Y1),(X2,Y2), …,(Xn,Yn)。对于平面中的这n个点,可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看,这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为:使总的拟合误差(即总残差)达到最小。有以下三个标准可以选择:
(1)用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
(2)用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
(3)最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外,得到的估计量还具有优良特性。这种方法对异常值非常敏感。
最常用的是普通最小二乘法( Ordinary Least Square,OLS):所选择的回归模型应该使所有观察值的残差平方和达到最小
数学公式表达:Q为残差平方和——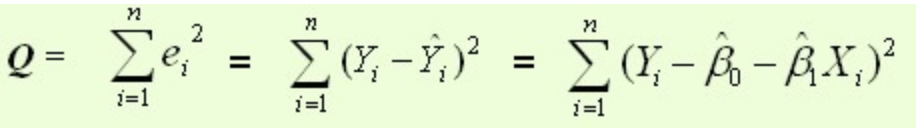
要使得Q最小,即求Q得极值。把![]() 看做变量,然后对
看做变量,然后对![]() 求偏导,可得:
求偏导,可得:

然后对上述两个偏导进一步消元、计算可得:
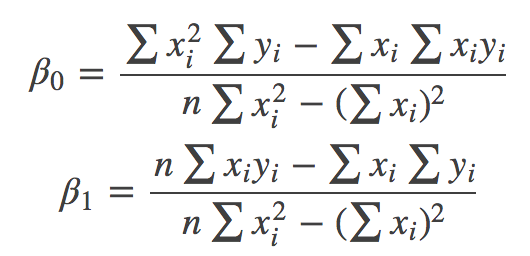
这样我们就可以确定![]() ,得到回归模型。最后将数据代入带这个模型中,即可得到我们要的结果。
,得到回归模型。最后将数据代入带这个模型中,即可得到我们要的结果。
2. 多元线性回归
推广到更一般的情况,假如有更多的模型变量 x1,x2,⋯,xn,可以用线性函数表示如下:
![]()
对于m个样本来说,可以用如下线性方程组表示:
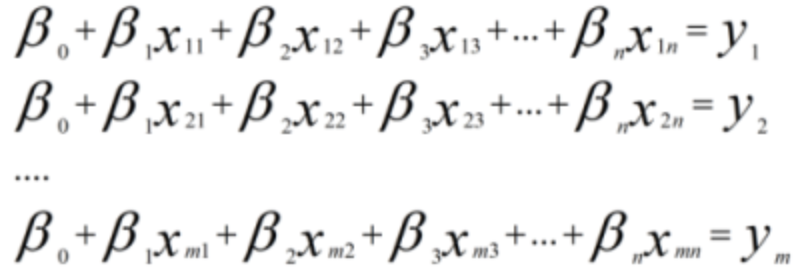
如果将样本矩阵xij记为矩阵A,将参数矩阵记为向量β,真实值记为向量Y,上述线性方程组可以表示为:
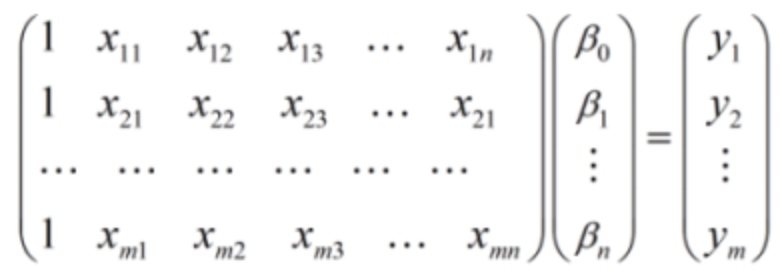 即
即 ![]()
对于最小二乘来说,最终的矩阵表达形式可以表示为:
![]() (这里涉及到向量范式)
(这里涉及到向量范式)
其中m≥n,由于考虑到了常数项,故属性值个数由n变为n+1
该方程的求解过程如下:
![]()
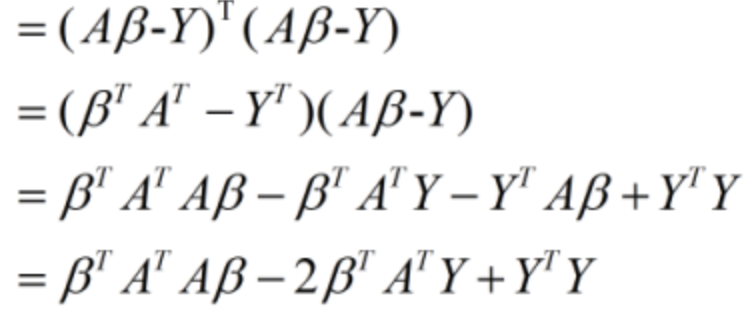
其中倒数第二行中的中间两项为标量,所以二者相等。然后利用该式对向量β求导:
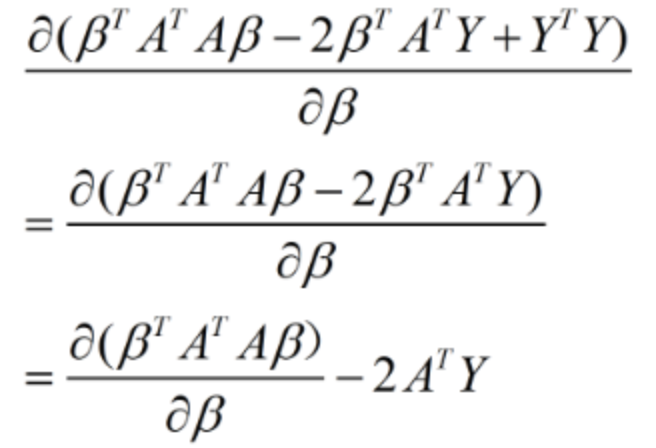 ①
①

令上式结果等于0可得:
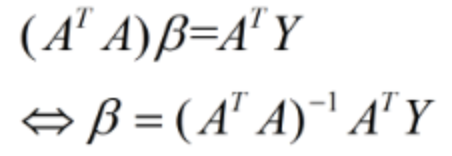 ②
②
注:(1)式是根据向量矩阵求导公式求导得到后面的式子
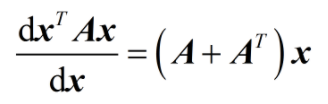
三、 最小二乘法和梯度下降算法
1. 二者相同点
最小二乘法和梯度下降法在线性回归问题中的目标函数是一样的(或者说本质相同),都是通过最小化均方误差来构建拟合曲线。
2. 二者不同点
见下表:
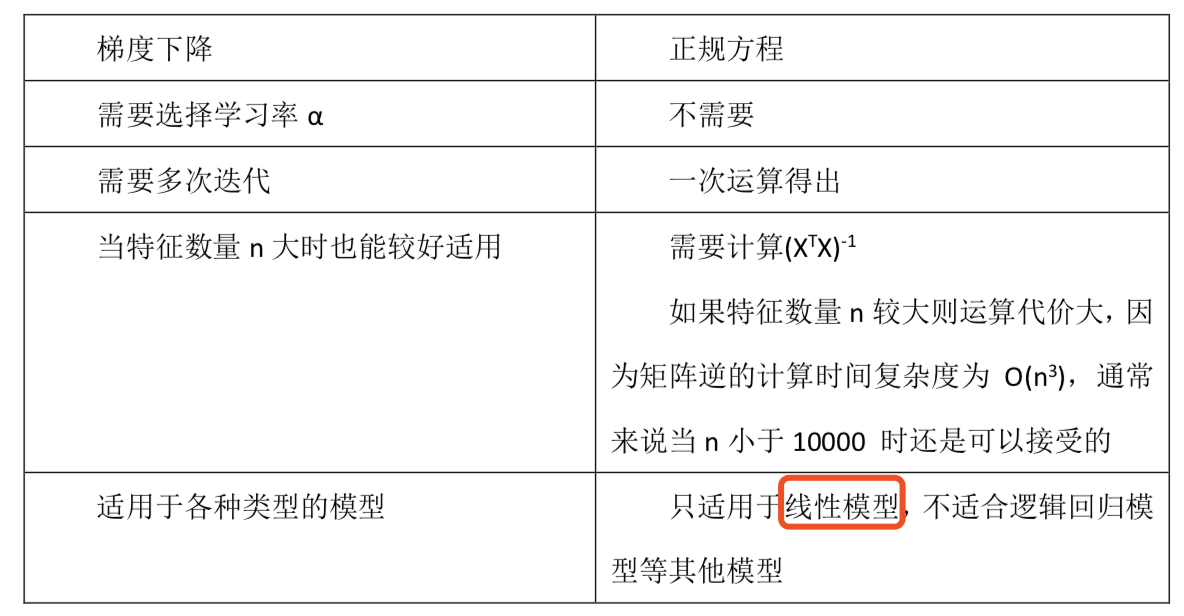
梯度下降适用性极强,一般而言,只要是凸函数,都可以通过梯度下降法得到全局最优值(对于非凸函数,能够得到局部最优解)
最小二乘法只适用于线性模型(这里一般指线性回归)
3. 最小二乘法中需要注意的问题
(1)②式中的  不可逆问题
不可逆问题
关于ATA在什么情况下不可逆:
1)当样本的数量小于参数向量(即β)的维度时,此时ATA一定是不可逆的。例如:你有1000个特征,但你的样本数目小于1000的话,那么构造出的ATA就是不可逆的。
2)在所有特征中若存在一个特征与另一个特征线性相关或一个特征与若干个特征线性相关时,此时ATA也是不可逆的
如何解决不可逆问题:
1)筛选出线性无关的特征,不保留相同的特征,保证不存在线性相关的特征。
2)增加样本量。
3)采用正则化的方法。对于正则化的方法,常见的是L1正则项和L2正则项,L1项有助于从很多特征中筛选出重要的特征,而使得不重要的特征为0(所以L1正则项是个不错的特征选择方法);如果采用L2正则项的话,实际上解析解就变成了如下的形式:

λ即正则参数(是一种超参数)后面的矩阵为(n+1)*(n+1)维,如果不考虑常数项的话,就是一个单位阵;此时括号中的矩阵一定是可逆的。
(2)最小二乘法的改进——加权最小二乘法
最小二乘法由于是最小化均方差,所以它考虑了每个样本的贡献,也就是每个样本具有相同的权重;
由于它采用距离作为度量,使得他对噪声比较敏感(最小二乘法假设噪声服从高斯分布),即使得他它对异常点比较敏感。
因此,人们提出了加权最小二乘法,相当于给每个样本设置了一个权重,以此来反应样本的重要程度或者对解的影响程度
参考:https://blog.csdn.net/qll125596718/article/details/8248249
https://www.cnblogs.com/wangkundentisy/p/7505487.html