Some questions
神经网络的结构,即几层网络,输入输出怎么设计才最有效?
设计几层网络比较好的问题仍然是个黑匣子,没有理论支撑应该怎么设计网络,现在仍是经验使然。
数学理论证明,三层的神经网络就能够以任意精度逼近任何非线性连续函数。那么为什么还需要有深度网络?
深层网络一般用于深度学习范畴,一般的分类、回归问题还是传统机器学习算法用的比较多,而深度学习的天空在cv、nlp等需要大量数据的领域。
在不同应用场合下,激活函数怎么选择?
没深入研究过,感觉还是靠经验多一些;
学习率怎么怎么选择?
学习率的原则肯定是开始大收敛快,后面小逼近全局最优,需要设置动态的学习率。而且最开始的学习率设置大了训练会震荡,设置小了收敛会很慢,这是实际项目中需要调的超参数。
训练次数设定多少训练出的模型效果更好?
关于训练次数的问题,一般设置检查点然后让训练到模型过拟合,选择检查点中保存的最优模型权重就好了。次数要能够使得模型过拟合,因为不过拟合就没有达到模型的极限。
The Unknown Word
| The First Column | The Second Column |
|---|---|
| LSTM | Long-Short Term Memory 长短时期记忆单元 |
| fine-tunning | 微调 |
| DBN | Deep Belief Network 深度信念网络 |
| unsupervised layer-wise training | 无监督逐层训练 |
| weight sharing | 全共享 |
#coding:utf-8
import random
import math
#
# 参数解释:
# "pd_" :偏导的前缀
# "d_" :导数的前缀
# "w_ho" :隐含层到输出层的权重系数索引
# "w_ih" :输入层到隐含层的权重系数的索引
class NeuralNetwork:
LEARNING_RATE = 0.5
def __init__(self, num_inputs, num_hidden, num_outputs, hidden_layer_weights = None, hidden_layer_bias = None, output_layer_weights = None, output_layer_bias = None):
self.num_inputs = num_inputs
self.hidden_layer = NeuronLayer(num_hidden, hidden_layer_bias)
self.output_layer = NeuronLayer(num_outputs, output_layer_bias)
self.init_weights_from_inputs_to_hidden_layer_neurons(hidden_layer_weights)
self.init_weights_from_hidden_layer_neurons_to_output_layer_neurons(output_layer_weights)
def init_weights_from_inputs_to_hidden_layer_neurons(self, hidden_layer_weights):
weight_num = 0
for h in range(len(self.hidden_layer.neurons)):
for i in range(self.num_inputs):
if not hidden_layer_weights:
self.hidden_layer.neurons[h].weights.append(random.random())
else:
self.hidden_layer.neurons[h].weights.append(hidden_layer_weights[weight_num])
weight_num += 1
def init_weights_from_hidden_layer_neurons_to_output_layer_neurons(self, output_layer_weights):
weight_num = 0
for o in range(len(self.output_layer.neurons)):
for h in range(len(self.hidden_layer.neurons)):
if not output_layer_weights:
self.output_layer.neurons[o].weights.append(random.random())
else:
self.output_layer.neurons[o].weights.append(output_layer_weights[weight_num])
weight_num += 1
def inspect(self):
print('------')
print('* Inputs: {}'.format(self.num_inputs))
print('------')
print('Hidden Layer')
self.hidden_layer.inspect()
print('------')
print('* Output Layer')
self.output_layer.inspect()
print('------')
def feed_forward(self, inputs):
hidden_layer_outputs = self.hidden_layer.feed_forward(inputs)
return self.output_layer.feed_forward(hidden_layer_outputs)
def train(self, training_inputs, training_outputs):
self.feed_forward(training_inputs)
# 1. 输出神经元的值
pd_errors_wrt_output_neuron_total_net_input = [0] * len(self.output_layer.neurons)
for o in range(len(self.output_layer.neurons)):
# ∂E/∂zⱼ
pd_errors_wrt_output_neuron_total_net_input[o] = self.output_layer.neurons[o].calculate_pd_error_wrt_total_net_input(training_outputs[o])
# 2. 隐含层神经元的值
pd_errors_wrt_hidden_neuron_total_net_input = [0] * len(self.hidden_layer.neurons)
for h in range(len(self.hidden_layer.neurons)):
# dE/dyⱼ = Σ ∂E/∂zⱼ * ∂z/∂yⱼ = Σ ∂E/∂zⱼ * wᵢⱼ
d_error_wrt_hidden_neuron_output = 0
for o in range(len(self.output_layer.neurons)):
d_error_wrt_hidden_neuron_output += pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].weights[h]
# ∂E/∂zⱼ = dE/dyⱼ * ∂zⱼ/∂
pd_errors_wrt_hidden_neuron_total_net_input[h] = d_error_wrt_hidden_neuron_output * self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_input()
# 3. 更新输出层权重系数
for o in range(len(self.output_layer.neurons)):
for w_ho in range(len(self.output_layer.neurons[o].weights)):
# ∂Eⱼ/∂wᵢⱼ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢⱼ
pd_error_wrt_weight = pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].calculate_pd_total_net_input_wrt_weight(w_ho)
# Δw = α * ∂Eⱼ/∂wᵢ
self.output_layer.neurons[o].weights[w_ho] -= self.LEARNING_RATE * pd_error_wrt_weight
# 4. 更新隐含层的权重系数
for h in range(len(self.hidden_layer.neurons)):
for w_ih in range(len(self.hidden_layer.neurons[h].weights)):
# ∂Eⱼ/∂wᵢ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢ
pd_error_wrt_weight = pd_errors_wrt_hidden_neuron_total_net_input[h] * self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_weight(w_ih)
# Δw = α * ∂Eⱼ/∂wᵢ
self.hidden_layer.neurons[h].weights[w_ih] -= self.LEARNING_RATE * pd_error_wrt_weight
def calculate_total_error(self, training_sets):
total_error = 0
for t in range(len(training_sets)):
training_inputs, training_outputs = training_sets[t]
self.feed_forward(training_inputs)
for o in range(len(training_outputs)):
total_error += self.output_layer.neurons[o].calculate_error(training_outputs[o])
return total_error
class NeuronLayer:
def __init__(self, num_neurons, bias):
# 同一层的神经元共享一个截距项b
self.bias = bias if bias else random.random()
self.neurons = []
for i in range(num_neurons):
self.neurons.append(Neuron(self.bias))
def inspect(self):
print('Neurons:', len(self.neurons))
for n in range(len(self.neurons)):
print(' Neuron', n)
for w in range(len(self.neurons[n].weights)):
print(' Weight:', self.neurons[n].weights[w])
print(' Bias:', self.bias)
def feed_forward(self, inputs):
outputs = []
for neuron in self.neurons:
outputs.append(neuron.calculate_output(inputs))
return outputs
def get_outputs(self):
outputs = []
for neuron in self.neurons:
outputs.append(neuron.output)
return outputs
class Neuron:
def __init__(self, bias):
self.bias = bias
self.weights = []
def calculate_output(self, inputs):
self.inputs = inputs
self.output = self.squash(self.calculate_total_net_input())
return self.output
def calculate_total_net_input(self):
total = 0
for i in range(len(self.inputs)):
total += self.inputs[i] * self.weights[i]
return total + self.bias
# 激活函数sigmoid
def squash(self, total_net_input):
return 1 / (1 + math.exp(-total_net_input))
def calculate_pd_error_wrt_total_net_input(self, target_output):
return self.calculate_pd_error_wrt_output(target_output) * self.calculate_pd_total_net_input_wrt_input();
# 每一个神经元的误差是由平方差公式计算的
def calculate_error(self, target_output):
return 0.5 * (target_output - self.output) ** 2
def calculate_pd_error_wrt_output(self, target_output):
return -(target_output - self.output)
def calculate_pd_total_net_input_wrt_input(self):
return self.output * (1 - self.output)
def calculate_pd_total_net_input_wrt_weight(self, index):
return self.inputs[index]
# 文中的例子:
nn = NeuralNetwork(2, 2, 2, hidden_layer_weights=[0.15, 0.2, 0.25, 0.3], hidden_layer_bias=0.35, output_layer_weights=[0.4, 0.45, 0.5, 0.55], output_layer_bias=0.6)
for i in range(10000):
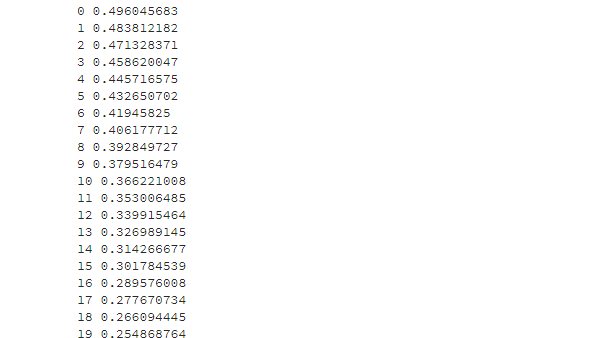
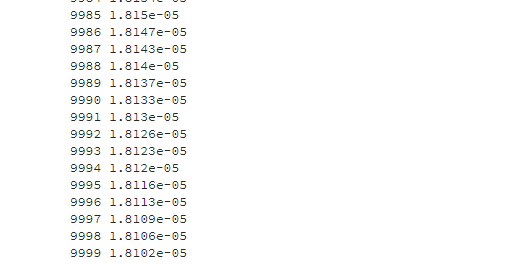
nn.train([0.05, 0.1], [0.01, 0.09])
print(i, round(nn.calculate_total_error([[[0.05, 0.1], [0.01, 0.09]]]), 9))
#另外一个例子,可以把上面的例子注释掉再运行一下:
# training_sets = [
# [[0, 0], [0]],
# [[0, 1], [1]],
# [[1, 0], [1]],
# [[1, 1], [0]]
# ]
# nn = NeuralNetwork(len(training_sets[0][0]), 5, len(training_sets[0][1]))
# for i in range(10000):
# training_inputs, training_outputs = random.choice(training_sets)
# nn.train(training_inputs, training_outputs)
# print(i, nn.calculate_total_error(training_sets))

Reference
transmission
transmission_Back_Algorithm
Transmission_Online_demonstration_of_neural_network_changes
Transmission_How_The_Backpropagation_algorithm_works