算法思想
/*
----------------中缀转后缀 前缀 概念---------
后缀-----同级操作符按 左优先原则
前缀-----右优先原则
中缀表达式 前缀表达式 后缀表达式
a+b +ab ab+
A+B*(C-D)-E/F +A-*B-CD/EF ABCD-*+EF/-
A+B-C*D/E+F AB+CD*E/-F+
----------------转后缀--------------
扫描中缀表达式
遇到操作数 直接加入后缀表达式;
遇到括号
"(" 直接入栈;
")" 弹出栈中运算符到后缀表达式 遇到"("为止;
遇到运算符
弹出栈中优先级高 或与当前运算符相等 的所有运算符加入后缀表达式;
期间遇到"("或栈空则停止 把当前运算符入栈;
扫描结束
弹出剩余操作符 到后缀表达式
----------------计算--------------
扫描后缀表达式
遇到操作数 入栈;
遇到运算符 弹出栈顶两个元素进行运算 运算结果 入栈;
*/
代码
#include "Algorithm_bracket.h"
int weight(char c) // 单引号是字符型 双引号是字符串型
{
if(c=='+' || c=='-')
{
return 2;
}
else if( c=='*' || c=='/')
{
return 3;
}
if( c=='(' )
{
return -1;
}
}
bool GetTop(Stack S, char &x)
{
if(isEmpty(S))
{
return false;
}
x = S.str[S.top];
return true;
}
bool TransPostfix(char instr[], char Pstr[])
{
Stack S;
InitStack(S); // 栈 用于存放操作符
int n = 0;
for(int i=0; i<strlen(instr); i++) // 扫描
{
//printf("i: %i c: %c Pstr: %s\n", i, instr[i], Pstr);
char c = instr[i];
if(c == '(') // 入栈
{
Push(S, c);
}
else if(c == ')') // 弹出所有操作符 直到遇到 "("
{
char x;
Pop(S, x);
while(x != '(')
{
Pstr[n++] = x;
Pop(S, x);
}
}
else if(c=='+' || c=='-' || c=='*' || c=='/')
{
if(isEmpty(S))
{
Push(S, c);
}
else
{
// 弹出优先级 高于等于 c优先级的运算符
char x;
GetTop(S, x);
while(weight(x) >= weight(c) && !isEmpty(S)) // 遇到"("权重为最小的-1 或栈空则停止;
{
Pop(S, x);
Pstr[n++] = x;
GetTop(S, x);
}
// 当前操作符入栈
Push(S, c);
}
}
else // 遇到操作数
{
Pstr[n++] = c;
}
}
if(isEmpty(S))
{
return false;
}
// 弹出剩余操作符 到后缀表达式
while(! isEmpty(S))
{
char x;
Pop(S, x);
Pstr[n++] = x;
}
return true;
}
int main()
{
char instr[Maxsize];
char Pstr[Maxsize]; // 存放后缀表达式
puts("Please input a infix str:");
scanf("%s", &instr);
TransPostfix(instr, Pstr);
puts("The postfix str:");
printf("%s", Pstr);
return 0;
}
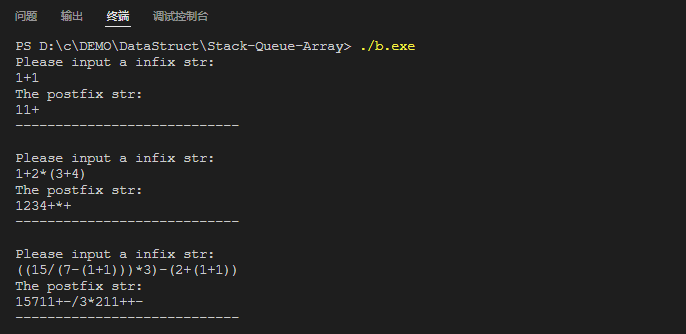
测试