什么是动态规划,我们要如何描述它?
动态规划算法通常基于一个递推公式及一个或多个初始状态。 当前子问题的解将由上一次子问题的解推出。使用动态规划来解题只需要多项式时间复杂度, 因此它比回溯法、暴力法等要快许多。
现在让我们通过一个例子来了解一下DP的基本原理。
首先,我们要找到某个状态的最优解,然后在它的帮助下,找到下一个状态的最优解。
“状态”代表什么及如何找到它?
“状态"用来描述该问题的子问题的解。原文中有两段作者阐述得不太清楚,跳过直接上例子。
如果我们有面值为1元、3元和5元的硬币若干枚,如何用最少的硬币凑够11元? (表面上这道题可以用贪心算法,但贪心算法无法保证可以求出解,比如1元换成2元的时候)
首先我们思考一个问题,如何用最少的硬币凑够i元(i<11)?为什么要这么问呢? 两个原因:1.当我们遇到一个大问题时,总是习惯把问题的规模变小,这样便于分析讨论。 2.这个规模变小后的问题和原来的问题是同质的,除了规模变小,其它的都是一样的, 本质上它还是同一个问题(规模变小后的问题其实是原问题的子问题)。
好了,让我们从最小的i开始吧。当i=0,即我们需要多少个硬币来凑够0元。 由于1,3,5都大于0,即没有比0小的币值,因此凑够0元我们最少需要0个硬币。 (这个分析很傻是不是?别着急,这个思路有利于我们理清动态规划究竟在做些什么。) 这时候我们发现用一个标记来表示这句“凑够0元我们最少需要0个硬币。”会比较方便, 如果一直用纯文字来表述,不出一会儿你就会觉得很绕了。那么, 我们用d(i)=j来表示凑够i元最少需要j个硬币。于是我们已经得到了d(0)=0, 表示凑够0元最小需要0个硬币。当i=1时,只有面值为1元的硬币可用, 因此我们拿起一个面值为1的硬币,接下来只需要凑够0元即可,而这个是已经知道答案的, 即d(0)=0。所以,d(1)=d(1-1)+1=d(0)+1=0+1=1。当i=2时, 仍然只有面值为1的硬币可用,于是我拿起一个面值为1的硬币, 接下来我只需要再凑够2-1=1元即可(记得要用最小的硬币数量),而这个答案也已经知道了。 所以d(2)=d(2-1)+1=d(1)+1=1+1=2。一直到这里,你都可能会觉得,好无聊, 感觉像做小学生的题目似的。因为我们一直都只能操作面值为1的硬币!耐心点, 让我们看看i=3时的情况。当i=3时,我们能用的硬币就有两种了:1元的和3元的( 5元的仍然没用,因为你需要凑的数目是3元!5元太多了亲)。 既然能用的硬币有两种,我就有两种方案。如果我拿了一个1元的硬币,我的目标就变为了: 凑够3-1=2元需要的最少硬币数量。即d(3)=d(3-1)+1=d(2)+1=2+1=3。 这个方案说的是,我拿3个1元的硬币;第二种方案是我拿起一个3元的硬币, 我的目标就变成:凑够3-3=0元需要的最少硬币数量。即d(3)=d(3-3)+1=d(0)+1=0+1=1. 这个方案说的是,我拿1个3元的硬币。好了,这两种方案哪种更优呢? 记得我们可是要用最少的硬币数量来凑够3元的。所以, 选择d(3)=1,怎么来的呢?具体是这样得到的:d(3)=min{d(3-1)+1, d(3-3)+1}。
OK,码了这么多字讲具体的东西,让我们来点抽象的。从以上的文字中, 我们要抽出动态规划里非常重要的两个概念:状态和状态转移方程。
上文中d(i)表示凑够i元需要的最少硬币数量,我们将它定义为该问题的"状态", 这个状态是怎么找出来的呢?我在另一篇文章 动态规划之背包问题(一)中写过: 根据子问题定义状态。你找到子问题,状态也就浮出水面了。 最终我们要求解的问题,可以用这个状态来表示:d(11),即凑够11元最少需要多少个硬币。 那状态转移方程是什么呢?既然我们用d(i)表示状态,那么状态转移方程自然包含d(i), 上文中包含状态d(i)的方程是:d(3)=min{d(3-1)+1, d(3-3)+1}。没错, 它就是状态转移方程,描述状态之间是如何转移的。当然,我们要对它抽象一下,
d(i)=min{ d(i-vj)+1 },其中i-vj >=0,vj表示第j个硬币的面值;
有了状态和状态转移方程,这个问题基本上也就解决了。当然了,Talk is cheap,show me the code!
伪代码如下:

下图是当i从0到11时的解:

从上图可以得出,要凑够11元至少需要3枚硬币。
此外,通过追踪我们是如何从前一个状态值得到当前状态值的, 可以找到每一次我们用的是什么面值的硬币。比如,从上面的图我们可以看出, 最终结果d(11)=d(10)+1(面值为1),而d(10)=d(5)+1(面值为5),最后d(5)=d(0)+1 (面值为5)。所以我们凑够11元最少需要的3枚硬币是:1元、5元、5元。
注意:原文中这里本来还有一段的,但我反反复复读了几遍, 大概的意思我已经在上文从i=0到i=3的分析中有所体现了。作者本来想讲的通俗一些, 结果没写好,反而更不好懂,所以这段不翻译了。
我们还是说算法导论里的例子:
Description:
The rod-cutting problem is the following. Given a rod of length n inches and a table of prices pi for i D 1,2,…,n, determine the maximum revenue rn obtainable by cutting up the rod and selling the pieces. Note that if the price pn for a rod of length n is large enough, an optimal solution may require no cutting at all.
以下给出的样例:
Analysis:
长度为n的钢条可以有2n-1中切割方案,所以当n很大时用暴力求解的方法是行不通的。假设将该钢条切割成k(k的取值为[1,n])段,切割顺序为从钢条的左端开始,那么最有切割方案是:
n = len1+len2+len3+…+lenk
将钢条切割为长度是len1,len2,…,lenk的小段,得到最大收益
rn = p len1+p len2+p len3+…+p lenk
根据样例给出的价格表,可以得到最大收益值ri(i=1,2,…,10)及对应的切割方案。
|
i |
最大收益 |
切割方案 |
|
1 |
1 |
无切割 |
|
2 |
5 |
无切割 |
|
3 |
8 |
无切割 |
|
4 |
10 |
4 = 2 + 2 |
|
5 |
13 |
5 = 2 + 3 |
|
6 |
17 |
无切割 |
|
7 |
18 |
7 = 1 + 6 或7 = 2 + 2 + 3 |
|
8 |
22 |
8 = 2 + 6 |
|
9 |
25 |
9 = 3 + 6 |
|
10 |
30 |
无切割
|
由上表可以得出:长度为n的钢条其最大收益值和长度为k和n-k的两条钢条的最大收益值相关。
我们可以假设长度为n的钢条的最大收益值:
rn = max(pn,r1+rn-1,r2+rn-2,…,rn-1+r1),pn为不切割时的价格。
这样可以通过组合两个相关子问题的最优解,并在所有可能的两段切割方案中选取组合收益最大者,构成原问题的最优解。
另一种思路:将钢条从左边切割长度为i的一段,只对右边剩下的长度为n-i的一段继续进行切割(递归求解),对左边的一段则不再进行分割。
rn = max(pi + rn-i) (i取值范围[1,n])
在这个公式中,原问题的最优解只包含一个相关子问题(右端剩余部分)的解。
自顶向下的递归算法实现
1 //自顶向下递归实现,prof[]是样例给出的价格表 2 int cutRod(int prof[], int n) 3 { 4 if (n == 0) 5 return 0; 6 else 7 { 8 int profit = 0; 9 for (int i = 1; i <= n; i++) 10 profit = max(profit, prof[i] + cutRod(prof, n - i)); 11 return profit; 12 } 13 14 }
根据代码可以分析得出:
随着n的增大,程序的运行时间会成倍的增加。原因是,cutRod反复地用相同的参数值对自身进行递归调用,即它反复求解相同的子问题。
当 n = 4时,递归调用树如下:
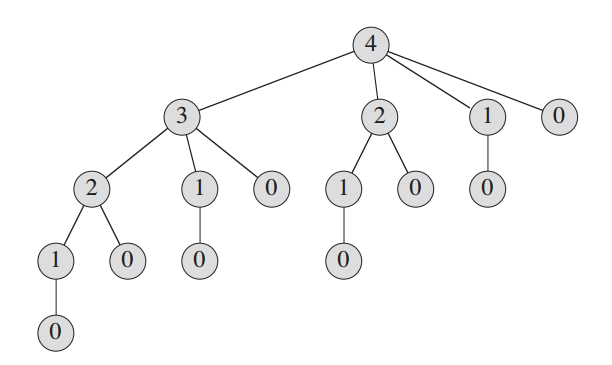
cutRod的运行时间为n的指数函数,T(n)= 2n
使用动态规划方法求解钢条切割的最优化问题
我们可以用备忘录的方式:
1、带备忘的自顶向下法
备忘就是一张存储每次计算最佳收益的表,这样就可以避免“自顶向下递归算法”中出现的重复计算重叠子问题的情况
1 int memoizedCutRodAux(int pro[], int r[], int n) 2 { 3 if (r[n] > 0) 4 return r[n]; 5 else 6 { 7 int profit = 0; 8 for (int i = 1; i <= n; i++) 9 profit = max(profit, pro[i] + memoizedCutRodAux(pro, r, n - i)); 10 r[n] = profit; 11 return profit; 12 } 13 }
2、自底向上法(javascript版本)
1 function Cut(p, n) { 2 var m = []; 3 var s = []; 4 5 for (var i = 1; i <= n; i++) { 6 m[i] = []; 7 s[i] = []; 8 for (var j = 1; j <= n; j++) { 9 m[i][j] = 0; 10 s[i][j] = 0; 11 } 12 } 13 14 15 for (var l = 0; l < n; l++) { 16 17 for (var i = 1; i + l <= n; i++) { 18 19 var j = i + l; 20 21 m[i][j] = p[l] ? p[l] : 0; 22 23 for (var k = i; k < j; k++) { 24 25 var temp = m[i][k] + m[k + 1][j]; 26 27 if (temp > m[i][j]) { 28 m[i][j] = temp; 29 s[i][j] = k; 30 } 31 } 32 33 } 34 } 35 return { 36 m: m, 37 s: s 38 }; 39 40 }
总结:结合动态规划的算法设计步骤来说,钢条切割问题也是遵守其标准的。
第一步先确定最优化解的结构特征:最优切割方案是由第一次切割后得到的两段钢条的最优切割方案组成的,或者是第一次切割后,其右端剩余部分的最优切割方案组成的。
第二步递归定义最优解的值,由上面的分析我们可以得到rn = max(pn,r1+rn-1,r2+rn-2,…,rn-1+r1)和rn = max(pi + rn-i) 两个最优解的公式,其满足求得原问题最优解的条件。
第三步根据得到的求最优解公式,计算出结果。我们用到了两种方法:带备忘的自顶向下递归法和自底向上法(非递归)。
第四步构造出最优解。