摘要:List item使用scikit-learn机器学习包的支持向量机算法,使用全部特征对鸢尾花进行分类。
本文分享自华为云社区《支持向量机算法之鸢尾花特征分类【机器学习】》,作者:上进小菜猪。
一.前言
1.1 本文原理
支持向量机(SVM)是一种二元分类模型。它的基本模型是在特征空间中定义最大区间的线性分类器,这使它不同于感知器;支持向量机还包括核技术,这使得它本质上是一个非线性分类器。支持向量机的学习策略是区间最大化,它可以形式化为求解凸二次规划的问题,等价于正则化铰链损失函数的最小化。支持向量机的学习算法是求解凸二次规划的优化算法。Scikit learn(sklearn)是机器学习中常见的第三方模块。它封装了常见的机器学习方法,包括回归、降维、分类、聚类等。
1.2 本文目的
- List item使用scikit-learn机器学习包的支持向量机算法,使用全部特征对鸢尾花进行分类;
- 使用scikit-learn机器学习包的支持向量机算法,设置SVM对象的参数,包括kernel、gamma和C,分别选择一个特征、两个特征、三个特征,写代码对鸢尾花进行分类;
- 使用scikit-learn机器学习包的支持向量机算法,选择特征0和特征2对鸢尾花分类并画图,gamma参数分别设置为1、10、100,运行程序并截图,观察gamma参数对训练分数(score)的影响,请说明如果错误调整gamma参数会产生什么问题?
二.实验过程
2.1 支持向量机算法SVM
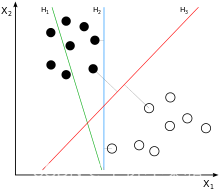
实例的特征向量(以2D为例)映射到空间中的一些点,如下图中的实心点和空心点,它们属于两个不同的类别。支持向量机的目的是画一条线来“最好”区分这两类点,这样,如果将来有新的点,这条线也可以很好地进行分类。
2.2List item使用scikit-learn机器学习包的支持向量机算法,使用全部特征对鸢尾花进行分类;
首先引入向量机算法svm模块:
from sklearn import svm
还是老样子,使用load_iris模块,里面有150组鸢尾花特征数据,我们可以拿来进行学习特征分类。
如下代码:
from sklearn.datasets import load_iris iris = load_iris() X = iris.data print(X.shape, X) y = iris.target print(y.shape, y)
下面使用sklearn.svm.SVC()函数。
C-支持向量分类器如下:
svm=svm.SVC(kernel='rbf',C=1,gamma='auto')
使用全部特征对鸢尾花进行分类
svm.fit(X[:,:4],y)
输出训练得分:
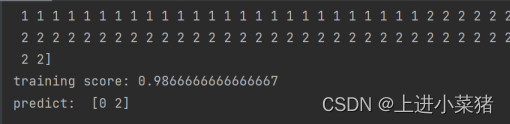
print("training score:",svm.score(X[:,:4],y)) print("predict: ",svm.predict([[7,5,2,0.5],[7.5,4,7,2]]))
使用全部特征对鸢尾花进行分类训练得分如下:
2.3 使用scikit-learn机器学习包的支持向量机算法,设置SVM对象的参数,包括kernel、gamma和C,分别选择一个特征、两个特征、三个特征,写代码对鸢尾花进行分类;
2.3.1 使用一个特征对鸢尾花进行分类
上面提过的基础就不再写了。如下代码:

使用一个特征对鸢尾花进行分类,如下代码:
svm=svm.SVC()
svm.fit(X,y)
输出训练得分:
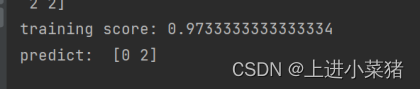
print("training score:",svm.score(X,y)) print("predict: ",svm.predict([[7,5,2,0.5],[7.5,4,7,2]]))
使用一个特征对鸢尾花进行分类训练得分如下:
2.3.2 使用两个特征对鸢尾花进行分类
使用两个特征对鸢尾花进行分类,如下代码:
svm=svm.SVC() svm.fit(X[:,:1],y)
输出训练得分:
print("training score:",svm.score(X[:,:1],y)) print("predict: ",svm.predict([[7],[7.5]]))
使用两个特征对鸢尾花进行分类训练得分如下:

2.3.3 使用三个特征对鸢尾花进行分类
使用三个特征对鸢尾花进行分类,如下代码:
svm=svm.SVC(kernel='rbf',C=1,gamma='auto') svm.fit(X[:,1:3],y)
输出训练得分:
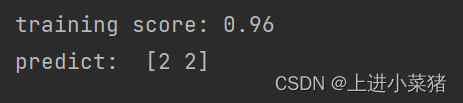
print("training score:",svm.score(X[:,1:3],y)) print("predict: ",svm.predict([[7,5],[7.5,4]]))
使用三个特征对鸢尾花进行分类训练得分如下:
2.3.4 可视化三个特征分类结果
使用plt.subplot()函数用于直接指定划分方式和位置进行绘图。
x_min,x_max=X[:,1].min()-1,X[:,1].max()+1 v_min,v_max=X[:,2].min()-1,X[:,2].max()+1 h=(x_max/x_min)/100 xx,vy =np.meshgrid(np.arange(x_min,x_max,h),np.arange(v_min,v_max,h)) plt.subplot(1,1,1) Z=svm.predict(np.c_[xx.ravel(),vy.ravel()]) Z=Z.reshape(xx.shape)
绘图,输出可视化。如下代码
plt.contourf(xx,vy,Z,cmap=plt.cm.Paired,alpha=0.8) plt.scatter(X[:, 1], X[:, 2], c=y, cmap=plt.cm.Paired) plt.xlabel('Sepal width') plt.vlabel('Petal length') plt.xlim(xx.min(), xx.max()) plt.title('SVC with linear kernel') plt.show()
可视化三个特征分类结果图:

2.4使用scikit-learn机器学习包的支持向量机算法,选择特征0和特征2对鸢尾花分类并画图,gamma参数分别设置为1、10、100,运行程序并截图,观察gamma参数对训练分数(score)的影响,请说明如果错误调整gamma参数会产生什么问题?
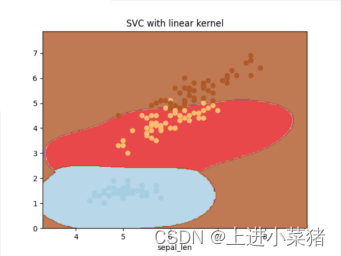
2.4.1当gamma为1时:
讲上文的gamma='auto‘ 里的auto改为1,得如下代码:
svm=svm.SVC(kernel='rbf',C=1,gamma='1') svm.fit(X[:,1:3],y)
运行上文可视化代码,得如下结果:

2.4.2当gamma为10时:
讲上文的gamma='auto‘ 里的auto改为10,得如下代码:
svm=svm.SVC(kernel='rbf',C=1,gamma='10') svm.fit(X[:,:3:2],y)
运行上文可视化代码,得如下结果:


2.4.3当gamma为100时:
讲上文的gamma='auto‘ 里的auto改为100,得如下代码:
svm=svm.SVC(kernel='rbf',C=1,gamma='100') svm.fit(X[:,:3:2],y)
运行上文可视化代码,得如下结果:
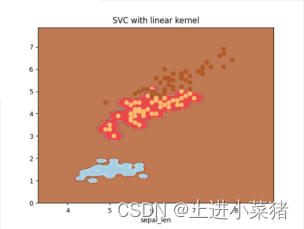

2.4.4 结论
参数gamma主要是对低维的样本进行高度度映射,gamma值越大映射的维度越高,训练的结果越好,但是越容易引起过拟合,即泛化能力低。通过上面的图可以看出gamma值越大,分数(score)越高。错误使用gamma值可能会引起过拟合,太低可能训练的结果太差。