带你了解两种线性规划的方法：稀疏矩阵存储和预处理

摘要：本文为大家带来线性规划的稀疏矩阵存储和数据预处理。

本文分享自华为云社区《线性规划--稀疏矩阵》，原文作者：Bale10 。

随着AI时代的发展，线性规划问题的规模越来越大是一种必然。面对大规模的线性规划问题，如何存储数据，使得存储空间节省以避免资源的浪费，并且使得数据的查询、修改和增删方便快捷，是一个急需解决的问题。本文为大家带来线性规划的稀疏矩阵存储和数据预处理。

稀疏矩阵

LP的规模通常是由约束矩阵A的规模决定的，矩阵的元素通常用8个字节的double型储存，假设矩阵有m行，n列，则直接储存A需要8mn字节。如果A有10000行，20000列（不是特别大规模的），那么需要1.6G内存储存A，一方面内存要求高，另一方面对矩阵A的操作困难。大规模LP通常含有大量的零元，非零元占比非常小，这个性质称为稀疏性，即A为稀疏矩阵。

稀疏矩阵储存

稀疏矩阵的数据结构设计应该考虑下面三个因素：

1. 仅存非零元，一个好的稀疏矩阵数据结构应该仅存A的非零元，而不存大量的零元。这样做的优点有三。首先，节省内存，使得大型稀疏矩阵能存在内存中。其次，若仅存非零元内存也放不下，则必须借助于外存，而从外存存取数据的速度一般比从内存存取数据慢得多，因此，在使用外存的情况我们也希望仅存非零元。第三，涉及零元的操作可以不执行，从而显著节约计算时间。
2. 非零元的产生--填入元，一个稀疏矩阵，在高斯消去(或LU分解）过程中，原来的零元可能要变成非零元。这种在消去过程中，由零元变成的非零元，叫做填入元；在整个消去过程中产生的填入元的个数，叫做填入量。如果一个十分稀疏的矩阵，经过上述消去运算后产生大量的填入元，则稀疏性就会消失，因此，保持矩阵的稀疏性是利用其稀疏性的前提。如何设法使消去过程中产生尽可能少的填入元是算法需要考虑的。稀疏矩阵是一个动态的数据结构，特别是经常需要插入非零元或删去非零元。因此，一个好的稀疏矩阵数据结构必须便于插入或删除。
3. 稀疏矩阵的数据结构和消去算法紧密相关，在考虑稀疏矩阵的数据结构时，必须同时考虑到消去算法，数据结构必须尽可能便于其算法的实现。

线性表

最简单的稀疏矩阵存储方案是线性表。为了具体起见，我们以下列稀疏矩阵A_5为例：

将非零元按列存放到数组CE中：

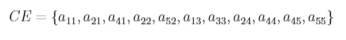
CE中相应非零元的行号记录在数组IROW中：

为了给出每个非零元在的列号，引入一个指针数组ICFR，ICFR(j)表示第j列第一个非零元在CE中的位置。

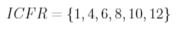
ICFR的长度为N+1，ICFR(N+1)表示最后一个元存放在第$N$列末元位置加1的位置上，这是为了便于计算最后一列非零元个数而引入的。这种存储方案所需要存储量为2NZ+N+1。它的优点是存储量小，结构简单，单缺点是不便于插入和删除，若要插入一个非零元，位于它下面的非零元必须向下移动一个位置，这是非常浪费时间的。

在程序中为了允许插入非零元，通常要说明一个较大的数组。上述是将A按列存放，当然也可以按行存放。经常的做法是先将A进行LU分解，然后将下三角形矩阵L按列存放，上三角矩阵U按行存放。

单链表

为了克服线性表不便于插入和删除的缺点，引入链表数据结构。即在上述线性表中增加一个链表指针数组LNXT，LNXT(i)表示第i个非零元的下一个非零元的位置，同时用数组ICNZ记录給列非零元的个数。这种链形表称为单链表，又称为列链表。仍然以上述稀疏矩阵A_5为例，并按列存放：

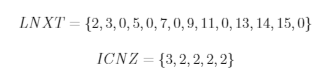
从上述表结构可以看出，对稀疏矩阵的每一非零元，表中有一个三元组(行号，元素，下一个元素位置)，即

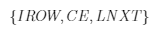
每列非零元，均以链指针$LNXT$连起来，每列最后一个非零元，链指针为0，表示链的结束。而指针数组$ICFR$指示每列的首元位置。

1. 同一列非零元不一定要挨着存放，因为每个非零元均用$LNXT$指出下一个元的位置，所以下一个元可以放在表中任何位置。
2. 插入和删除一个元，不需要移动其它元素，只需要改变指针。

采用链表的优点是便于插入或删除；缺点是访问链表中任何一个元均需要从一列的第一个非零元开始顺序找下去，而且均需要间接访问，所以比访问线性表要慢。

双链表

双链表是在单链表基础上增加ICOL(i)第i个非零元列号，RNXT(i)第i个非零元行链指针，即该行下一非零元的位置，以及IRFR(i)第i行的第一个非零元在链表中的位置。

这种双链表数据结构对于处理结构不对称的稀疏矩阵是十分方便的，它具有单链表的优点，即便于插入和删去。

在双链表中插入或删除一个元的操作和单链表时相同，只需注意插入或删除一个元不仅要修改列链和空单元链，而且要修改行链。

设计好稀疏矩阵的数据结构是稀疏矩阵算法的关键之一。好的稀疏矩阵数据结构，不仅要节约存储，而且要便于查找、插入和删除，以及便于稀疏矩阵算法的实现。数据结构对算法设计有根本性影响。通常先用链表建立稀疏矩阵，并进行一次假高斯消去、插入填入元、求出非零元总数，然后转换为线性表，以便快速进行求解。

数据预处理

线性规划问题的规模越来越大，含有成千上万个约束和变量的问题非常常见，面临着数据的储存和处理效率问题，大规模问题一般都是由模型支持工具自动生成的，往往存在大量冗余的约束和变量，在算法求解之前进行数据预处理是必要的。

主要目的

1. 化约冗余约束，减少约束矩阵非零元素，提高稀疏度，减少问题规模，节省内存；
2. 改善模型的数值特征，提高问题的数值稳定性；
3. 在不求解问题的情况下判定问题无可行解或无界。

主要挑战

1. 提升复杂预处理方法的性能；
2. 确定不同预处理方法的作用次序和作用次数；
3. 确定预处理何时停止；
4. 设计预处理并行框架。

预处理方法

不可行性

空行和空列

固定变量

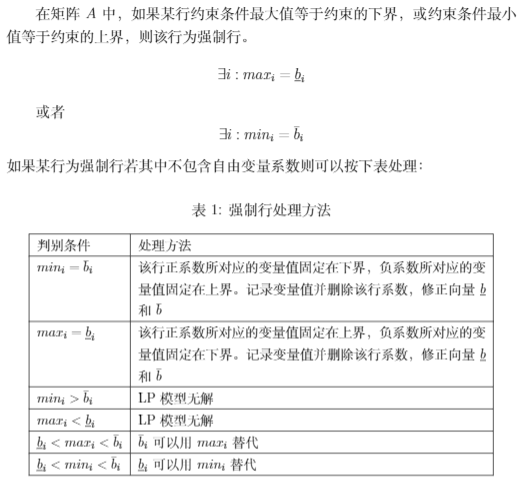
强制行

比例行

平行行

对偶规定

两行非零元消去

 

点击关注，第一时间了解华为云新鲜技术~