2017年10月icpc 哈尔滨赛——A题题解（马拉车算法）

直接上题目：

Alice like strings, especially long strings. For each string, she has a special evaluation system to judge how elegant the string is. She defines that a string  S[1..3n−2](n≥2) is one-and-half palindromic if and only if it satisfies  S[i]=S[2n−i]=S[2n+i−2](1≤i≤n) .For example,  abcbabc  is one-and-half palindromic string, and  abccbaabc  is not. Now, Alice has generated some long strings. She ask for your help to find how many substrings which is one-and-half palindromic.

输入描述:

The first line is the number of test cases. For each test case, there is only one line containing a string(the length of strings is less than or equal to 500000), this string only consists of lowercase letters.

输出描述:

For each test case, output a integer donating the number of one-and-half palindromic substrings.

示例1

输入

1
ababcbabccbaabc

输出

2

说明

In the example input, there are two substrings which are one-and-half palindromic strings, abab and abcbabc.


题意很简单，算是一到”水题“（相对于别人是）
题意：
  输入T个样咧，每个样例包含若干字符，，然后从这个字符串里找出若干个符合条件的子字符串，输出个数，符合条件：S[i]=S[2n−i]=S[2n+i−2](1≤i≤n) 
  eg：abcbabc 中abcba和cbabc分别为回文串就符合条件
思路：找中心点呗，，找两个中心点可以互达的两个回文串

           a b a b c b a b c c b a a b c   p[i]
回文长度：   0 1 1 0 2 0 2 0 0 0 0 0 0 0 0
显而易见可以有：abab 和abcbabc两个符合条件

枚举后面那个点 找到[i-p[i],i-1]有多少个数可以到当前点
维护前面每一个点最远可达位置 i+p[i];
找到[i-p[i],i-1]有多少个最远可达位置 >=i;

区间[l,r]大于x的数的个数 可持久线段树log
N st
L 往左
R 往右
出口 1，N
最少修改 次数使得走

运用马拉车（Manacher's Algorithm 马拉车算法）：

这个马拉车算法Manacher‘s Algorithm是用来查找一个字符串的最长回文子串的线性方法，由一个叫Manacher的人在1975年发明的，这个方法的最大贡献是在于将时间复杂度提升到了线性，这是非常了不起的。对于回文串想必大家都不陌生，就是正读反读都一样的字符串，比如 "bob", "level", "noon" 等等，那么如何在一个字符串中找出最长回文子串呢，可以以每一个字符为中心，向两边寻找回文子串，在遍历完整个数组后，就可以找到最长的回文子串。但是这个方法的时间复杂度为O(n*n)，并不是很高效，下面我们来看时间复杂度为O(n)的马拉车算法。

由于回文串的长度可奇可偶，比如"bob"是奇数形式的回文，"noon"就是偶数形式的回文，马拉车算法的第一步是预处理，做法是在每一个字符的左右都加上一个特殊字符，比如加上'#'，那么

bob    -->    #b#o#b#

noon    -->    #n#o#o#n# 

这样做的好处是不论原字符串是奇数还是偶数个，处理之后得到的字符串的个数都是奇数个，这样就不用分情况讨论了，而可以一起搞定。接下来我们还需要和处理后的字符串t等长的数组p，其中p[i]表示以t[i]字符为中心的回文子串的半径，若p[i] = 1，则该回文子串就是t[i]本身，那么我们来看一个简单的例子：

# 1 # 2 # 2 # 1 # 2 # 2 #
1 2 1 2 5 2 1 6 1 2 3 2 1

由于第一个和最后一个字符都是#号，且也需要搜索回文，为了防止越界，我们还需要在首尾再加上非#号字符，实际操作时我们只需给开头加上个非#号字符，结尾不用加的原因是字符串的结尾标识为''，等于默认加过了。通过p数组我们就可以找到其最大值和其位置，就能确定最长回文子串了，那么下面我们就来看如何求p数组，需要新增两个辅助变量mx和id，其中id为最大回文子串中心的位置，mx是回文串能延伸到的最右端的位置，这个算法的最核心的一行如下：

 

p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;

 

可以这么说，这行要是理解了，那么马拉车算法基本上就没啥问题了，那么这一行代码拆开来看就是

如果mx > i, 则 p[i] = min(p[2 * id - i], mx - i)

否则， p[i] = 1

当 mx - i > P[j] 的时候，以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中，由于 i 和 j 对称，以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中，所以必有 P[i] = P[j]，见下图。

 

 

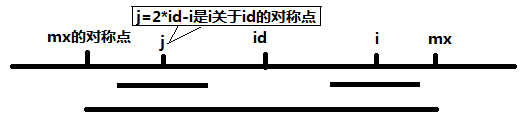
当 P[j] >= mx - i 的时候，以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中，但是基于对称性可知，下图中两个绿框所包围的部分是相同的，也就是说以S[i]为中心的回文子串，其向右至少会扩张到mx的位置，也就是说 P[i] >= mx - i。至于mx之后的部分是否对称，就只能老老实实去匹配了。

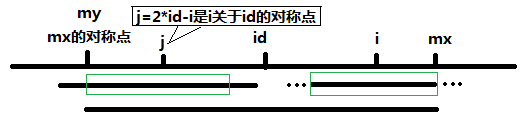
对于 mx <= i 的情况，无法对 P[i]做更多的假设，只能P[i] = 1，然后再去匹配了。

#include <vector>
#include <iostream>
#include <string>

using namespace std;

string Manacher(string s) {
// Insert '#'
string t = "$#";
for (int i = 0; i < s.size(); ++i) {
t += s[i];
t += "#";
}
// Process t
vector<int> p(t.size(), 0);
int mx = 0, id = 0, resLen = 0, resCenter = 0;
for (int i = 1; i < t.size(); ++i) {
p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
while (t[i + p[i]] == t[i - p[i]]) ++p[i];
if (mx < i + p[i]) {
mx = i + p[i];
id = i;
}
if (resLen < p[i]) {
resLen = p[i];
resCenter = i;
}
}
return s.substr((resCenter - resLen) / 2, resLen - 1); //获得字符串s中 从第(rescenter-reslen)/2位开始的长度为reslen-1的字符串

                                                        //默认时的长度为从开始位置到尾
}

int main() {
string s1 = "12212";
cout << Manacher(s1) << endl;
string s2 = "122122";
cout << Manacher(s2) << endl;
string s = "waabwswfd";
cout << Manacher(s) << endl;
}

算法有了，可还不够哦，还需要一点东西：可持续化线段树（这里先不写，线段树会分出开单独记）

是不是觉得思路贼简单，有种你就写代码：（大佬给的，自己现在还是写不出来的）

#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N=5e5+10;
const LL INF=1e18+10;
const double eps=1e-6;

char a[N],str[N];
int p[N];
void manacher(int l)
{
    int i,j=0,k,ans=0;
    //for(i=1;i<=l;++i)str[i<<1]=s[i],str[(i<<1)+1]='#';
    //str[1]='#';str[l*2+1]='#';str[0]='&';str[l*2+2]='$';
    //l=l*2+1;j=0;
    for(int i=1;i<=l;i++)str[i]=a[i];
    str[0]='&';str[l+1]='$';
    for(i=1;i<=l;)
    {
       while(str[i-j-1]==str[i+j+1])++j;
       p[i]=j;if(j>ans)ans=j;
       for(k=1;k<=j&&p[i]-k!=p[i-k];++k)p[i+k]=min(p[i-k],p[i]-k);
       i+=k;j=max(j-k,0);
    }
}
int n;
struct Chairmantree
{
    int rt[N*30],ls[N*30],rs[N*30],sum[N*30];
    int tot;
    void init()
    {
        tot=0;
    }
    void build(int l,int r,int &pos)
    {
        pos=++tot;
        sum[pos]=0;
        if(l==r)return;
        int mid=(l+r)>>1;
        build(l,mid,ls[pos]);
        build(mid+1,r,rs[pos]);
    }
    void update(int p,int c,int pre,int l,int r,int &pos)
    {
        pos=++tot;
        ls[pos]=ls[pre];
        rs[pos]=rs[pre];
        sum[pos]=sum[pre]+c;
        if(l==r)return;
        int mid=(l+r)>>1;
        if(p<=mid)
            update(p,c,ls[pre],l,mid,ls[pos]);
        else
            update(p,c,rs[pre],mid+1,r,rs[pos]);
    }
    int query(int s,int t,int L,int R,int l,int r)
    {
        if(L<=l&&r<=R)
            return sum[t]-sum[s];
        int mid=(l+r)>>1;
        int ans=0;
        if(L<=mid)
            ans+=query(ls[s],ls[t],L,R,l,mid);
        if(R>mid)
            ans+=query(rs[s],rs[t],L,R,mid+1,r);
        return ans;
    }
};
Chairmantree tree;
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%s",a+1);
        n=strlen(a+1);
        manacher(n);
        LL ans=0;
        tree.init();
        tree.build(1,n,tree.rt[0]);
        for(int i=1;i<=n;i++)
            tree.update(i+p[i],1,tree.rt[i-1],1,n,tree.rt[i]);
        for(int i=1;i<=n;i++)
        {
            if(!p[i])continue;
            ans+=tree.query(tree.rt[i-p[i]-1],tree.rt[i-1],i,n,1,n);
        }
        printf("%lld
",ans);
        for(int i=0;i<=tree.tot;i++)
            tree.rt[i]=0,tree.ls[i]=0,tree.rs[i]=0,tree.sum[i]=0;
    }
    return 0;
}

就这样算不算补题啊！