论文《一种模式识别神经网络重力匹配算法》2007中提出模式识别的方法进行重力匹配。通过概率神经网络处理重力测量值序列,结合惯性导航系统的轨迹与重力背景图,在重力背景图中找出一组与重力测量值最为相似的重力序列,以此作为重力匹配的结果。
论文匹配方法原理如下图所示:
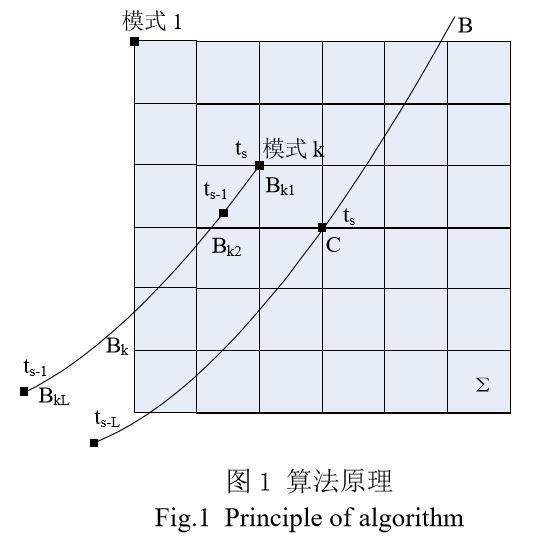
通过在重力背景图搜索区域中平移惯性导航系统给出的轨迹,得到对应的重力值序列,作为模式k的特征向量。详情见论文。
在测试过程中,假设重力测量值误差非常小(几乎为0)时,才可能得到更精确的重力匹配结果。并且论文中的节点偏置系数(如下图所示)对模式识别的结果影响很大。若该系数设置不当,可能无法得到正确的重力匹配结果,在使用过程中需要斟酌。

MATLAB代码如下所示:
% 《一种模式识别神经网络重力匹配算法》 % 利用概率神经网络进行重力匹配 clear all; clc; %% 训练数据 load x2; load y2; load z2; M=3; %搜索区域左右间隔 N=3; %上下间隔 load Storedata_caiyang; %真实轨迹 load INS_caiyang; %INS轨迹 load g_m; %重力测量值 % 相对位置关系 L=length(INS_caiyang); % 采样点个数 del_lamda=zeros(L-1,1); % 相邻两个采样点之间的经度相对距离 del_fai=zeros(L-1,1); % 纬度相对距离 for i=1:L-1 del_lamda(i)=abs(INS_caiyang(L,1)-INS_caiyang(L-i,1)); %经度 del_fai(i)=abs(INS_caiyang(L,2)-INS_caiyang(L-i,2)); %纬度 end center_point=zeros(1,2); center_point=INS_caiyang(L,1:2); % 以INS轨迹最后一个点为搜索区域的中心 center_num=find_num(center_point); %在重力背景图中的坐标 % 定义第k个模式类 S = (2*M+1)*(2*N+1); %共S个模式类 P = zeros(L,S); Bk_num=zeros(1,2); g_k = zeros(L,1); %重力值序列 for k=1:S R1=floor(k/(2*N+1)); i_num(k) = center_num(1)-M+R1; % 搜索区域中,从上到下从左到右第k个网格点的横坐标 j_num(k) = center_num(2)+N-k+R1*(2*N+1)+1; % 纵坐标 lamda(k) = x2(1, i_num(k)); % 经纬度坐标 fai(k) = y2(j_num(k), 1); g_k(1) = z2(j_num(k),i_num(k)); % 对应重力背景图值 for j=1:L-1 Bk_lamda(j) = lamda(k) - del_lamda(j); % 根据相对位置计算k模式类轨迹上各点的经度 Bk_fai(j) = fai(k) - del_fai(j); % 纬度 point(1) = Bk_lamda(j); point(2) = Bk_fai(j); Bk_num= find_num(point); % 对应坐标 % 模式k对应的特征向量(重力值) g_k(j+1) = z2(Bk_num(2),Bk_num(1)); end % 输入矩阵P,包含重力值序列 P(:,k) = g_k(:); end % 模式指示矩阵T for i=1:S T(1,i) = i; end for i=1:L g_m_new(i, 1) = g_m(L-(i-1), 1); % 重力测量时间顺序:从后向前 end %% 神经网络参数 % 重力粗糙程度 start_point=zeros(1,2); % 搜索区域中心点 start_point=INS_caiyang(1,1:2); start_num=find_num(start_point); %在重力背景图中的坐标 X0 = center_num(1) - start_num(1); %轨迹跨越网格数 Y0 = center_num(2) - start_num(2); X = 2*M+X0; Y = 2*N+Y0; left_end_point(1) = start_num(1) - M; %搜索区域左上角顶点坐标 left_end_point(2) = start_num(2) - Y0 - N; % 经度方向 Q = 0; %粗糙度 for i=1:(X-1) for j=1:Y H1 = z2(left_end_point(2) + j -1,left_end_point(1) + i - 1); H2 = z2(left_end_point(2) + j -1,left_end_point(1) + (i+1) - 1); Q = Q + (H1 - H2)^2; end end Q_lamda = sqrt(1/((X-1)*Y)*Q); % 纬度方向 Q = 0; %粗糙度 for i=1:X for j=1:(Y-1) H1 = z2(left_end_point(2) + j -1,left_end_point(1) + i - 1); H2 = z2( left_end_point(2) + (j+1) -1,left_end_point(1) + i - 1); Q = Q + (H1 - H2)^2; end end Q_fai= sqrt(1/(X*(Y-1))*Q); sigma_z = (Q_lamda + Q_fai)/2; %平均粗糙度 %% 建立PNN p = P; T2 = ind2vec(T); % 生成单位矩阵 t = T2; spread = 0.5; %暂时用不到 net = newpnn_test(P, T2, spread); %% 利用样本训练和测试PNN x = g_m_new; y = net(x); %利用重力测量值测试神经网络 Yc = vec2ind(y); plot(INS_caiyang(:,1),INS_caiyang(:,2),'k'); hold on; plot(Storedata_caiyang(:,1),Storedata_caiyang(:,2),'r'); hold on; k = Yc; R1=floor(k/(2*N+1)); i_num(k) = center_num(1)-M+R1; %搜索区域中,从上到下从左到右第k个网格点的经度坐标 j_num(k) = center_num(2)+N-k+R1*(2*N+1)+1; %纬度 lamda(k) = x2(1, i_num(k)); %经纬度坐标 fai(k) = y2(j_num(k), 1); Bk(1,1) = lamda(k); Bk(1,2) = fai(k); for j=1:L-1 Bk_lamda(j) = lamda(k) - del_lamda(j); Bk_fai(j) = fai(k) - del_fai(j); point(1) = Bk_lamda(j); point(2) = Bk_fai(j); Bk_num= find_num(point); Bk(j,1:2) = point(1:2); end plot(Bk(:,1),Bk(:,2),'b'); hold on;
其中newpnn_test函数是根据MATLAB自带的newpnn修改得到的,主要修改了节点偏置部分的定义。MATLAB代码如下所示:
function out1 = newpnn_test(varargin) %NEWPNN Design a probabilistic neural network. % % Probabilistic neural networks are a kind of radial % basis network suitable for classification problems. % % <a href="matlab:doc newpnn">newpnn</a>(P,T,SPREAD) takes an RxQ input matrix P and an SxQ target matrix % T, a radial basis function SPREAD and returns a new probabilistic % neural network. % % If SPREAD is near zero the network will act as a nearest % neighbor classifier. As SPREAD becomes larger the designed % network will take into account several nearby design vectors. % % Here a classification problem is defined with a set of % inputs P and class indices Tc. A PNN is designed to fit this data. % % P = [1 2 3 4 5 6 7]; % Tc = [1 2 3 2 2 3 1]; % T = <a href="matlab:doc ind2vec">ind2vec</a>(Tc) % net = <a href="matlab:doc newpnn">newpnn</a>(P,T); % Y = net(P) % Yc = <a href="matlab:doc vec2ind">vec2ind</a>(Y) % % See also SIM, IND2VEC, VEC2IND, NEWRB, NEWRBE, NEWGRNN. % Mark Beale, 11-31-97 % Copyright 1992-2014 The MathWorks, Inc. %% ======================================================= % BOILERPLATE_START % This code is the same for all Network Functions. persistent INFO; if isempty(INFO), INFO = get_info; end if (nargin > 0) && ischar(varargin{1}) ... && ~strcmpi(varargin{1},'hardlim') && ~strcmpi(varargin{1},'hardlims') code = varargin{1}; switch code case 'info', out1 = INFO; case 'check_param' err = check_param(varargin{2}); if ~isempty(err), nnerr.throw('Args',err); end out1 = err; case 'create' if nargin < 2, error(message('nnet:Args:NotEnough')); end param = varargin{2}; err = nntest.param(INFO.parameters,param); if ~isempty(err), nnerr.throw('Args',err); end out1 = create_network(param); out1.name = INFO.name; otherwise, % Quick info field access try out1 = eval(['INFO.' code]); catch %#ok<CTCH> nnerr.throw(['Unrecognized argument: ''' code '''']) end end else [args,param] = nnparam.extract_param(varargin,INFO.defaultParam); [param,err] = INFO.overrideStructure(param,args); if ~isempty(err), nnerr.throw('Args',err,'Parameters'); end net = create_network(param); net.name = INFO.name; out1 = init(net); end end function v = fcnversion v = 7; end % BOILERPLATE_END %% ======================================================= function info = get_info info = nnfcnNetwork(mfilename,'Probabilistic Neural Network',fcnversion, ... [ ... nnetParamInfo('inputs','Input Data','nntype.data',{},... 'Input data.'), ... nnetParamInfo('targets','Target Data','nntype.data',{},... 'Target output data.'), ... nnetParamInfo('spread','Radial basis spread','nntype.strict_pos_scalar',0.1,... 'Distance from radial basis center to 0.5 output.'), ... ]); end function err = check_param(param) err = ''; end function net = create_network(param) % Data p = param.inputs; t = param.targets; if iscell(p), p = cell2mat(p); end if iscell(t), t = cell2mat(t); end % Dimensions [R,Q] = size(p); [S,Q] = size(t); % Architecture net = network(1,2,[1;0],[1;0],[0 0;1 0],[0 1]); %构建自定义神经网络 % Simulation net.inputs{1}.size = R; %输入维数R % 构造RBF net.inputWeights{1,1}.weightFcn = 'dist'; %输入与第一层连接权重,dist欧几里得函数 net.layers{1}.netInputFcn = 'netprod'; %输入函数:计算输入*权重求和的结果 net.layers{1}.transferFcn = 'radbas'; %传递函数(激活函数) net.layers{1}.size = Q; net.layers{2}.size = S; net.layers{2}.transferFcn = 'compet'; %竞争函数 net.outputs{2}.exampleOutput = t; % Weight and Bias Values % net.b{1} = zeros(Q,1)+sqrt(-log(.5))/param.spread; %节点偏置 zita = 0.3; % 节点偏置系数 sigma_z = 5.79; % 粗糙度 sigma = zita * sigma_z; net.b{1} = zeros(Q,1)+sigma; net.iw{1,1} = p'; %RBF输入权重(节点数据中心) net.lw{2,1} = t; %层之间权重 end
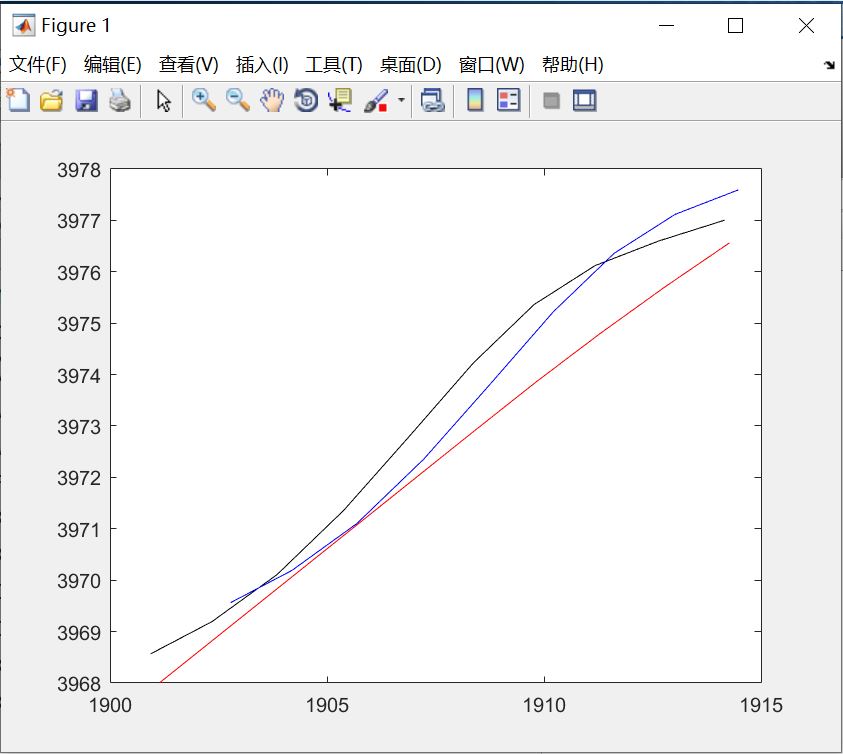
测试重力匹配结果如下图所示,其中红色为真实轨迹,黑色为惯性导航系统指示轨迹,蓝色为PNN匹配的轨迹: