人工智能深度学习入门练习之（34）深度学习 – 多层神经网络

深度学习 – 多层神经网络

单层网络

先回顾一下单层网络，即一个神经元（自适应线性单元），如下图所示。

可以使用梯度下降法训练模型，确定权重与偏置。

多层神经网络历史

深度学习涉及训练多层神经网络，也称为深度神经网络。

在20世纪50年代Rosenblatt感知器被开发出来之后，直到1986年hinton博士和他的同事开发了反向传播算法来训练多层神经网络，人们才重新对神经网络产生了兴趣。

现在，深度神经网络是一个热门技术，许多大公司，如百度，阿里，腾讯，谷歌，Facebook和微软，都在深度神经网络项目上投入巨资。

多层神经网络

神经网络其实就是按照一定规则连接起来的多个神经元。

上图展示了一个全连接(full connected, FC)神经网络，它的规则包括：

• 神经元按照层来布局。最左边的输入层，负责接收输入数据；最右边的输出层，负责输出数据。
• 中间是隐藏层，对于外部不可见。隐藏层可以包含多层，大于一层的就被称为深度神经网络，层次越多数据处理能力越强。
• 同一层的神经元之间没有连接。
• 前后两层的所有神经元相连(这就是full connected的含义)，前层神经元的输出就是后层神经元的输入。
• 每个连接都有一个权值。

上面这些规则定义了全连接神经网络的结构。事实上还存在很多其它结构的神经网络，比如卷积神经网络(CNN)、循环神经网络(RNN)，它们都具有不同的连接规则。

多层感知器(MLP)

一个完全连接的多层神经网络被称为多层感知器(MLP)，或深度前馈网络（deepfeedforwardnetwork）、前馈神经网络（feedforward neural network），是典型的深度学习模型。

层数和每层的神经元数被称为神经网络的超参数，由开发人员根据经验预先设置。

权重的调整训练还是通过梯度下降法来进行，但梯度的求取使用反向传播法。

多层神经网络的训练过程

多层神经网络的训练过程，按如下步骤进行：

1. 从输入层开始，将数据经过神经网络传输到输出层，这一步是前向传播。
2. 根据输出，计算误差(预测结果和已知结果之间的差异)，得到代价函数。利用梯度下降法最小化误差。
3. 梯度下降法需要计算每个权重的梯度，使用反向传播算法计算梯度，根据梯度调整权重值。

重复以上3个步骤训练权重。

与单层网络的区别

从大的方面来说，两者都是通过梯度下降法，求取代价函数的最小值，来训练权重。

区别在于，多层神经网络引入了反向传播算法来计算梯度。

单层网络中，权重的梯度计算是直接求代价函数对某个权重的偏导数，单层网络的代价函数相对简单，可以这样做。

但是多层神经网络中，越靠近输入层的权重，其代价函数越复杂，计算量非常大。而反向传播算法是一种高效简单的梯度算法。

深度学习 – 反向传播

梯度

一个深度神经网络的权重参数有可能会达到百万级，权重的梯度计算非常耗时，反向传播是一种非常高效的梯度算法。

一个神经网络中的所有权重参数可以表示为：

 

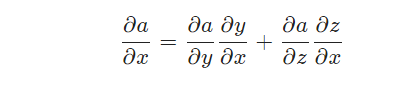
利用链式求导法则，计算代价函数相对于某个权重的偏导数（梯度），可以转化为这个权重之后所有层次的偏导数的表达式。

反向传播计算过程

反向传播由输出端往输入端逐层计算权重的梯度。

我们假设有下面这样3层神经网络：

神经元o1如下图所示：

设神经网络的代价函数为J(w)J(w), ww表示所有权重参数，根据链式法则，w5w5的梯度（偏导数）可以表示为：

理解反向传播算法

对于反向传播算法的理解，可以打个比方，一个公司一年的利润与目标差距比较大，公司开始找原因，看看谁的责任比较大。从管理层开始逐层往下找，确定每个人的责任(梯度)。反向传播算法，就是分黑锅，梯度是对偏差的贡献，就是黑锅。

深度学习 – 反向传播例子

为加深对反向传播算法的理解，本章将演示一个实际的权重计算例子。

考虑下面的神经网络:

上图中的神经网络包括以下部分:

• 2个输入
• 2个隐藏的神经元
• 2个输出神经元
• 2个偏置

下面是反向传播涉及的步骤:

• 步骤1: 前向传播
• 步骤2: 反向传播
• 步骤3: 权重值更新

步骤1: 前向传播

我们从前向传播开始。

我们将对输出层神经元重复这个过程，使用隐藏层神经元的输出作为输入。

现在，让我们看看最后的误差值是多少:

步骤2: 反向传播

现在，我们反向传播，计算出梯度。这样我们就可以通过权重值的调整来减少误差。

考虑W5，计算w5的梯度，调整w5的值。

因为我们是反向传播的，所以第一件事，是计算总误差对o1输出的变化率（导数）。

现在，我们将进一步向后传播，计算o1输出对o1总净输入的变化率（导数）。

现在让我们看看O1的总净输入对W5的变化率（导数）

步骤3: 权重值更新

现在，让我们把所有的值放在一起:

我们来计算W5的更新值:

• 同样，我们也可以计算其他权重值。
• 之后，我们将再次前向传播并计算输出、计算误差。
• 如果误差已经降到最小，我们将停止，否则我们将再次反向传播，并更新权重值。
• 这个过程将不断重复，直到误差降到最小。