人工智能深度学习入门练习之（32）深度学习 – 感知器

深度学习 – 人工神经元

关于人工神经元，前面章节稍微提过，本章将详细讨论。

生物神经元

人脑有数十亿个神经元。神经元是人脑中相互连接的神经细胞，参与处理和传递化学信号和电信号。树突是从其他神经元接收信息的分枝。

细胞核处理从树突接收到的信息。轴突是一种神经细胞用来传递信息的生物电缆。突触是轴突和其他神经元树突之间的连接。

人工神经元的出现

1943年，研究人员沃伦·麦卡洛克(Warren McCullock)和沃尔特·皮茨(Walter Pitts)发表了简化模拟脑细胞的首个概念设计，被称为McCullock-Pitts (MCP)神经元。他们将这种神经细胞描述为一个简单的逻辑门，输出二进制信息。

人脑神经元处理信息的过程：多个信号到达树突，然后整合到细胞体中，如果积累的信号超过某个阈值，就会产生一个输出信号，由轴突传递。

人工神经元

人工神经元是一个基于生物神经元的数学模型，神经元接受多个输入信息，对它们进行加权求和，再经过一个激活函数处理，然后将这个结果输出。

生物神经元对照人工神经元

生物神经元	人工神经元
细胞核	节点 (加权求和 + 激活函数)
树突	输入
轴突	带权重的连接
突触	输出

小结

人工神经元具有以下特点:

• 人工神经元是生物神经元的数学模型
• 它是人工神经网络中的一个基本单元
• 多个输入信息被加权求和
• 加权求和的结果经过一个激活函数后，生成输出信息
• 每个神经元连接到下一层神经元

深度学习 – 感知器原理

人工神经元也称为感知器。它接受输入信号，处理后再向一下层神经元输出信号。

感知器由Frank Rosenblatt在1957年提出，他介绍了一种基于人工神经元的感知器学习规则。

感知器定义

感知器的结构，如下图所示：

感知器中，输入信息被加权求和，再经过一个激活函数处理，然后生成输出信息。

假设正确的输出是预定义的，每次通过感知器传递数据时，都会将最终结果与正确的结果进行比较，并根据差值对感知器中的输入权重值进行调整，直到网络可以生成正确的最终输出。

所以，感知器的学习过程，实际上就是根据一组样本数据，确定感知器输入权重的过程。

感知器输入

一个感知器可以接受多个输入(x_1, x_2, …, x_n)(x1​,x2​,…,xn​)，每个输入都有一个权重值，另外还有一个偏置项(bias)，即上图中的w0，通常也记为b(bias)。

加权求和

对于输入信号，感知器首先会对其加权求和：

z(x) = w_0 + w_1x_1 + w_2x_2 + … + w_nx_nz(x)=w0​+w1​x1​+w2​x2​+…+wn​xn​

激活函数

激活函数作用是模拟生物神经元中阈值的作用，当信号强度达到阈值时，就输出信号，否则就没有输出。数学中的许多函数可以作为激活函数使用，例如阶跃函数(step funciton)，sign函数，sigmoid函数。

• 阶跃函数的输入信号大于t, 输出1，否则输出0。
• 符号（sign）函数的输入大于0，输出1，小于0，输出-1。
• Sigmoid函数是s曲线，输出值在0到1之间。

感知器的输出

感知器的输出，可以表示为:

输入

输入项：1, x_1, x_2, …, x_n1,x1​,x2​,…,xn​，表示为向量x

X = [1, x_1, x_2, …, x_n]X=[1,x1​,x2​,…,xn​]

权重

权重项：w_1, w_2, …, w_nw1​,w2​,…,wn​，表示为向量w

W = [w_0, w_1, w_2, …, w_n]W=[w0​,w1​,w2​,…,wn​]

偏置项(bias)

偏置项为 w_0 imes 1w0​×1，也记为bb

激活函数

激活函数为f(Z)f(Z)

输出

加权求和的值可以表示为:

Z = W · X = W^TX = sum _{i=0}^n w_i*x_iZ=W⋅X=WTX=i=0∑n​wi​∗xi​

经过激活函数处理后：

Y = f( W · X )Y=f(W⋅X)

例子：用感知器实现逻辑门

用感知器实现逻辑与

设计一个感知器，实现逻辑与功能。逻辑与函数，有两个输入，一个输出，真值表如下所示：

x1	x2	y
0	0	0
0	1	0
1	0	0
1	1	1

0表示false, 1表示true。

我们让权重：w0 = -0.8, w1 = 0.5, w2 = 0.5，激活函数使用阶跃函数(t=0)，这时，感知器就相当于and函数。

我们验算一下：

• x1 = 1, x2 = 1, y = x1 * w1 + x2 * w2 + w0 = 0.5*1 + 0.5*1 + (-0.8) = 0.2 > 0，输出为1，即true
• x1 = 0, x2 = 1, y = x1 * w1 + x2 * w2 + w0 = 0.5*0 + 0.5*1 + (-0.8) = -0.3 < 0，输出为0，即false

用感知器实现逻辑或

类似的，可以使用感知器实现逻辑或功能。

我们让权重：w0 = -0.3, w1 = 0.5, w2 = 0.5，激活函数使用阶跃函数(t=0)，这时，感知器就相当于or函数。

• x1 = 1, x2 = 1, y = x1 * w1 + x2 * w2 + w0 = 0.5*1 + 0.5*1 + (-0.3) = 0.7 > 0，输出为1，即true
• x1 = 0, x2 = 1, y = x1 * w1 + x2 * w2 + w0 = 0.5*0 + 0.5*1 + (-0.3) = 0.2 > 0，输出为1，即true

感知器还能做什么

事实上，感知器不仅仅能实现简单的布尔运算。它可以拟合任何的线性函数，任何线性分类或线性回归问题都可以用感知器来解决。

感知器训练

现在，你可能困惑前面的权重项和偏置项的值是如何获得的呢？

在感知器学习规则中，将实际输出与样本中的正确输出进行比较，根据输出偏差调整权重与偏置项。重复多次迭代样本数据，直到实际输出与正确输出匹配，从而得出正确的权重与偏置项，这就是感知器的学习过程。后面章节，将有更详细的介绍。

深度学习 – 感知器学习规则

如前所述，在 20 世纪 50 年代，感知器 (Rosenblatt, 1956, 1958) 成为第一个能根据每个类别的输入样本来学习权重的模型。约在同一时期，自适应线性单元 (adaptive linearelement, ADALINE) 简单地返回函数 f(x) 本身的值来预测一个实数 (Widrow and Hoff, 1960)，并且它还可以学习从数据预测这些数。

自适应线性单元(Adaline)的激活函数是一个线性函数，该函数的输出等于输入，实际上就相当于没有激活函数，线性激活函数$\phi (Z)$的定义：

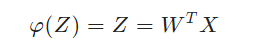
自适应线性单元的训练

自适应线性单元的训练规则

• 权重根据线性激活函数进行更新
• 将样本数据中的实际输出与线性激活函数的输出进行比较，计算模型偏差，然后更新权重。

感知器训练规则

• 权重是根据单位阶跃函数更新的
• 将样本数据中的实际输出与模型输出进行比较，计算模型偏差，然后更新权重。

自适应线性单元与感知器的区别，在于激活函数不同，自适应线性单元将返回一个实数值而不是0,1分类。因此自适应线性单元用来解决回归问题而不是分类问题。

自适应线性单元训练时，用于调节权重的训练算法是被称为梯度下降法。稍加改进后的随机梯度下降算法仍然是当今深度学习的主要训练算法。后面将详细介绍。

监督学习与无监督学习

监督学习：对有标记（分类）的训练样本进行学习，以尽可能对训练样本集外的数据进行标记（分类）预测。

监督学习中，所有的标记（分类）是已知的。因此，训练样本的岐义性低。

无监督学习：对没有标记（分类）的训练样本进行学习，以发现训练样本集中的结构性知识。

这里，所有的标记（分类）是未知的。因此，训练样本的岐义性高。

聚类就是典型的无监督学习，经过聚类后的样本数据就可以用来做监督学习。

目标函数

通常，神经网络的训练都属于监督学习类别，即使样本数据没有分类，也可先做聚类处理，把样本数据分类，然后就可以用来做监督学习了。

在监督学习下，对于一个样本，我们知道它的特征（输入）$x$，以及标记（输出）$y$。同时，我们还可以得到神经网络的预测输出$\hat{y}$。注意这里面我们用$y$表示训练样本里面的标记，也就是实际值；用$\hat{y}$表示神经网络的的预测值。我们当然希望预测值$\hat{y}$和实际值$y$越接近越好。

数学上有很多方法来表示预测值$\hat{y}$和实际值$y$接近程度，比如我们可以用$\hat{y}$和$y$的差的平方的$\genfrac{}{}{0ex}{}{1}{2}$来表示它们的接近程度

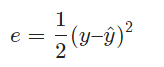
 我们把

$e$叫做单个样本的误差。至于为什么前面要乘$\genfrac{}{}{0ex}{}{1}{2}$，是为了后面计算方便。

训练数据中会有很多样本，比如$N$个，我们可以用训练数据中所有样本的误差的和，来表示神经网络的误差$E$，也就是

 上式的

$e^{(1)}$表示第一个样本的误差，$e^{(2)}$表示第二个样本的误差……。

上面的也可以表示为和式：

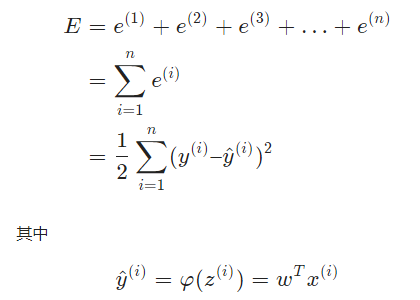
 x

${}^{(i)}$表示第$i$个训练样本的特征，$y^{(i)}$表示第$i$个样本的标记，我们也可以用元组$(x^{(i)},y^{(i)})$表示第$i$个训练样本。${\hat{y}}^{(i)}$则是神经网络对第$i$个样本的预测值，$\phi (z^{(i)})$中$z^{(i)}$表示第$i$个样本的加权求和值，$\phi (z)$表示线性激活函数。

对于一个训练数据集来说，我们当然希望误差$E$最小越好。对于特定的训练数据集来说，$(x^{(i)},y^{(i)})$的值都是已知的，所以$E$其实是参数$w$的函数。

w

$w$。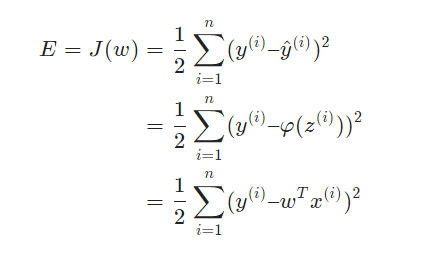

 由此可见，神经网络的训练，实际上就是求取到合适的权重

$w$，使差值$E$取得最小值。这在数学上称作优化问题，而$J(w)$就是我们优化的目标，称之为目标函数，也被称为代价函数、损失函数。

注意：前面提到，目标函数实际上是差值平方和，从数学上来说，平方与线性激活函数让目标函数变成可微凸函数。
对于可微凸函数，可以使用一种简单但功能强大的优化算法，梯度下降法来求取目标函数$J(w)$

的最小值，及其对应的参数

深度学习 – 激活函数

感知器中的激活函数模拟生物神经元中阈值的作用，当信号强度达到阈值时，就输出信号，否则就没有输出。数学中的许多函数可以作为激活函数使用，本章将详细介绍几种常用的激活函数。

激活函数的本质作用

从数学上来说，激活函数是用来加入非线性因素的，解决线性模型所不能解决的问题。
神经网络从数学上来看，是对函数的拟合，理论上已经证明，两层以上的神经网络可以逼近任意函数。

Sigmoid 函数

Sigmoid函数，即S形函数，是一个具有S形曲线的数学函数。Sigmoid函数是常用的激活函数。函数的数学定义如

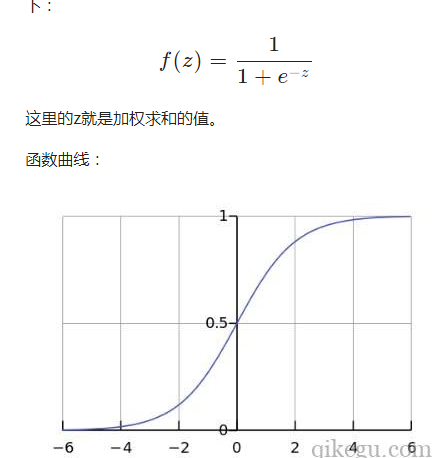
 可以看到Sigmoid 函数的值，总是在0到1之间。Sigmoid 函数的缺点是，在神经网络训练时，计算时间较长，速度比较慢。

ReLU/Rectifier函数 与 Softplus 函数

ReLU函数和Softplus函数也是常见的激活函数。这两个的函数曲线如下：

ReLU函数是目前深度神经网络中最常用的激活函数。

从函数曲线可以看出，ReLU函数的作用是，当输入信号小于0，没有输出；当输入信号大于0，按原样输出输入信号，也就是说ReLU函数祛除了负值的信号。

softplus函数与ReLU函数作用类似，softplus的曲线更平滑，softplus函数也被称为光滑的ReLU函数。

Softplus 函数的数学定义：

其他

其他还有 Softmax, Hyperbolic, sign等等激活函数，如需进一步了解可参考相关资料。

下图列举了常用的各种激活函数

如前所述，在 20 世纪 50 年代，感知器 (Rosenblatt, 1956, 1958) 成为第一个能根据每个类别的输入样本来学习权重的模型。约在同一时期，自适应线性单元 (adaptive linearelement, ADALINE) 简单地返回函数 f(x) 本身的值来预测一个实数 (Widrow and Hoff, 1960)，并且它还可以学习从数据预测这些数。

自适应线性单元(Adaline)的激活函数是一个线性函数，该函数的输出等于输入，实际上就相当于没有激活函数，线性激活函数$\phi (Z)$的定义：

$\phi (Z)=Z=W^{T}X$

自适应线性单元的训练

自适应线性单元的训练规则

• 权重根据线性激活函数进行更新
• 将样本数据中的实际输出与线性激活函数的输出进行比较，计算模型偏差，然后更新权重。

感知器训练规则

• 权重是根据单位阶跃函数更新的
• 将样本数据中的实际输出与模型输出进行比较，计算模型偏差，然后更新权重。

自适应线性单元与感知器的区别，在于激活函数不同，自适应线性单元将返回一个实数值而不是0,1分类。因此自适应线性单元用来解决回归问题而不是分类问题。

自适应线性单元训练时，用于调节权重的训练算法是被称为梯度下降法。稍加改进后的随机梯度下降算法仍然是当今深度学习的主要训练算法。后面将详细介绍。

监督学习与无监督学习

监督学习：对有标记（分类）的训练样本进行学习，以尽可能对训练样本集外的数据进行标记（分类）预测。

监督学习中，所有的标记（分类）是已知的。因此，训练样本的岐义性低。

无监督学习：对没有标记（分类）的训练样本进行学习，以发现训练样本集中的结构性知识。

这里，所有的标记（分类）是未知的。因此，训练样本的岐义性高。

聚类就是典型的无监督学习，经过聚类后的样本数据就可以用来做监督学习。

目标函数

通常，神经网络的训练都属于监督学习类别，即使样本数据没有分类，也可先做聚类处理，把样本数据分类，然后就可以用来做监督学习了。

在监督学习下，对于一个样本，我们知道它的特征（输入）$x$，以及标记（输出）$y$。同时，我们还可以得到神经网络的预测输出$\hat{y}$。注意这里面我们用$y$表示训练样本里面的标记，也就是实际值；用$\hat{y}$表示神经网络的的预测值。我们当然希望预测值$\hat{y}$和实际值$y$越接近越好。

数学上有很多方法来表示预测值$\hat{y}$和实际值$y$接近程度，比如我们可以用$\hat{y}$和$y$的差的平方的$\genfrac{}{}{0ex}{}{1}{2}$来表示它们的接近程度

$e=\genfrac{}{}{0ex}{}{1}{2}(y–^{)}^2$

我们把$e$叫做单个样本的误差。至于为什么前面要乘$\genfrac{}{}{0ex}{}{1}{2}$，是为了后面计算方便。

训练数据中会有很多样本，比如$N$个，我们可以用训练数据中所有样本的误差的和，来表示神经网络的误差$E$，也就是

$E=e^{(1)}+e^{(2)}+e^{(3)}+\dots +e^{(n)}$

上式的$e^{(1)}$表示第一个样本的误差，$e^{(2)}$表示第二个样本的误差……。

上面的也可以表示为和式：

$\begin{array}{rl}E& =e^{(1)}+e^{(2)}+e^{(3)}+\dots +e^{(n)}\\ & =\stackrel{n\sum }{i=1}{e}^{(i)}\\ & =\genfrac{}{}{0ex}{}{1}{2}\stackrel{n\sum }{i=1}(y^{(i)}–{\hat{y}}^{(i)}{)}^2\end{array}$

其中

${\hat{y}}^{(i)}=\phi (z^{(i)})=w^T{x}^{(i)}$

$x^{(i)}$表示第$i$个训练样本的特征，$y^{(i)}$表示第$i$个样本的标记，我们也可以用元组$(x^{(i)},y^{(i)})$表示第$i$个训练样本。${\hat{y}}^{(i)}$则是神经网络对第$i$个样本的预测值，$\phi (z^{(i)})$中$z^{(i)}$表示第$i$个样本的加权求和值，$\phi (z)$表示线性激活函数。

对于一个训练数据集来说，我们当然希望误差$E$最小越好。对于特定的训练数据集来说，$(x^{(i)},y^{(i)})$的值都是已知的，所以$E$其实是参数$w$的函数。