【ST表（RMQ）】

ST表

　　ST表是一种解决RMQ（区间最值问题）的强有力的工具

　　它可以做到O(nlogn)预处理，O(1)查询最值。

实现

　　ST表其实是一种倍增的思想，我们就拿取最大值为例：

开一个二维数组Max，其中Max[i][j]表示从第i位开始，包括第i位在内的2^j个数中最大的数，例如Max[i][1]表示第i个数和第i+1个数中大的那个数。

 

然后就类似于二分的样子，下一层也是拿两个已得到的区间的最大值作比较，然后存储。

预处理代码

for(int j=1;j<=21;j++)
    {
        for(int i=1;i+(1<<j)-1<=n;i++)
        {
            Max[i][j]=max(Max[i][j-1],Max[i+(1<<(j-1))][j-1]);
        }
    }

　　为什么要先循环j呢？因为我们是一层一层向上搜的，每一层的答案需要下面的基础，所以把j放在外层，然后(1<<(j-1)）就是把二进制的1向左移动（j-1）位，也就是2^(j-1)。

查询　　

　　查询也比较简单，我们只需要求出k=log2（r-l+1）(求2的k次幂小于这一段区间的值，并且尽可能大)，然后得到两个区间，比较就行了

 （图片来源）

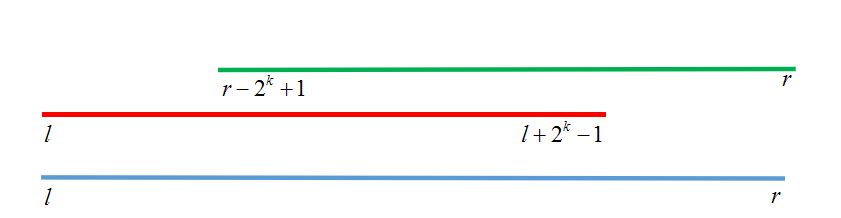
然后取最大值返回就可以了

int ST(int l,int r)
{
    int k=log2(r-l+1);
    return max(Max[l][k],Max[r-(1<<k)+1][k]);
}

既然了解了这么多，不如.......（放心，都是模板题）

洛谷P3865 【模板】ST表

#include<bits/stdc++.h>
#define N 100005
using namespace std;
int n,m;
int Max[N][21];
int ST(int l,int r)
{
    int k=log2(r-l+1);
    return max(Max[l][k],Max[r-(1<<k)+1][k]);
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&Max[i][0]);
    }
    for(int j=1;j<=21;j++)
    {
        for(int i=1;i+(1<<j)-1<=n;i++)
        {
            Max[i][j]=max(Max[i][j-1],Max[i+(1<<(j-1))][j-1]);
        }
    }
    int l,r;
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&l,&r);
        printf("%d
",ST(l,r));
    }
    return 0;
}

洛谷P2251 质量检测

// luogu-judger-enable-o2
#include<bits/stdc++.h>
#define N 100005
using namespace std;
int n,m;
int Min[N][21];
int ST(int l,int r)
{
    int k=log2(r-l+1);
    return min(Min[l][k],Min[r-(1<<k)+1][k]);
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&Min[i][0]);
    }
    for(int j=1;j<=21;j++)
    {
        for(int i=1;i+(1<<j)-1<=n;i++)
        {
            Min[i][j]=min(Min[i][j-1],Min[i+(1<<(j-1))][j-1]);
        }
    }
    for(int i=1;i+m-1<=n;i++)
    {
        printf("%d
",ST(i,i+m-1));
    }
    return 0;
}

洛谷P1816 忠诚

#include<bits/stdc++.h>
using namespace std;
int Min[100005][21];
int n,m;
int ST(int l,int r)
{
    int k=log2(r-l+1);
    return min(Min[l][k],Min[r-(1<<k)+1][k]);
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&Min[i][0]);
    }
    for(int j=1;j<=21;j++)
    {
        for(int i=1;i+(1<<j)-1<=n;i++)
        {
            Min[i][j]=min(Min[i][j-1],Min[i+(1<<(j-1))][j-1]);
        }
    }
    for(int i=1;i<=m;i++)
    {
        int l,r;
        scanf("%d%d",&l,&r);
        printf("%d ",ST(l,r));
    }
 }