1.完全二叉堆
分类: 最大堆和最小堆。
最大堆:父结点的键值总是大于或等于任何一个子节点的键值;
最小堆:父结点的键值总是小于或等于任何一个子节点的键值。
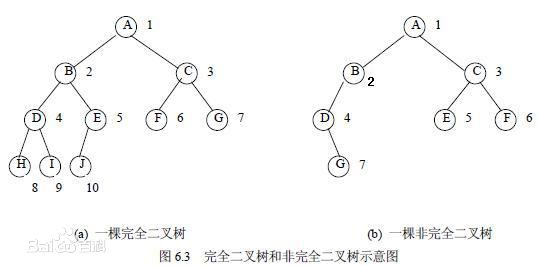
背景:完全二叉树
叶节点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树
完全二叉堆结构:
逻辑上,等同于完全二叉树;
物理上,直接借助向量实现。
计算节点位置:(以节点i 为例)
若存在父节点,父节点的位置为 (i-1)/2;
若存在左孩子,左孩子的位置为 i*2+1;(奇数)
若存在右孩子,右孩子的位置为 i*2+2;(偶数)
二叉堆的上滤(插入):[时间复杂度o(logn)]
1、当插入一个新元素时,放在最末尾。
2、若有父节点,将插入节点和父节点比较,如果插入节点大于父节点,交换位置。
3、重复2,直至插入节点不小于父节点或者没有父节点,上滤结束。
二叉堆的下滤(删除):
1、删除首元素,将最后一个元素移到首节点。
2、若有孩子,则比较该节点和最大孩子的值,若小于最大孩子的值,与最大的孩子互换位置。
3、重复2,直至该节点的值大于最大孩子的值或者没有孩子,下滤结束,堆序性得以满足。
二叉堆的建堆:
1、蛮力算法:(自上而下的上滤)
将每个元素插入到二叉堆,经过上滤调整组成二叉堆。
效率:时间复杂度o(nlogn),太大,完全可以做一个全排序。
2、自下而上的下滤(推荐)
从最后一个内部节点(有孩子的节点,公式(n/2-1))开始,进行下滤合并,再向前移一个节点,下滤合并直至首节点。
效率:时间复杂度o(n),节点内部所需调整的时间正比于高度,而不是深度。(高度越高,下滤时间就越长)
堆排序:
1、将数组中的元素,采用下滤的方式建堆。
2、将堆的首元素和末元素交换,最大的元素放在最后,前面组成一个新的堆,新堆的首元素下滤组成最大堆。
3、重复2,直至堆的规模变成1。
2.左式堆:
保持堆序性,附加单侧倾斜(节点分布偏向左侧,合并操作只涉及右侧)的新条件,来使堆的合并过程中只需调整很少的部分节点。
左式堆 的结构性:
在拓扑上不一定是完全二叉树,但是结构性并非堆结构的本质要求,可以牺牲掉。因此不采用向量,而是使用二叉树来实现。
空节点路径长度(NPL):
引入外部节点,外部节点的值为0。
npl(null) = 0
npl(x) = 1 + min( npl( lc(x) ), npl( rc(x) ) )
npl(x) = x到外部节点的最近距离;
npl(x) = x为根的最大满子树的高度。
左式堆的定义:
左倾:对任意节点x,都有npl( lc(x) ) > npl( rc(x) )
左式堆的任意一个子堆都是左式堆