You are given n points with integer coordinates on the plane. Points are given in a way such that there is no triangle, formed by any three of these n points, which area exceeds S.
Alyona tried to construct a triangle with integer coordinates, which contains all n points and which area doesn't exceed 4S, but, by obvious reason, had no success in that. Please help Alyona construct such triangle. Please note that vertices of resulting triangle are not necessarily chosen from n given points.
Input
In the first line of the input two integers n and S (3 ≤ n ≤ 5000, 1 ≤ S ≤ 1018) are given — the number of points given and the upper bound value of any triangle's area, formed by any three of given n points.
The next n lines describes given points: ith of them consists of two integers xi and yi ( - 108 ≤ xi, yi ≤ 108) — coordinates of ith point.
It is guaranteed that there is at least one triple of points not lying on the same line.
Output
Print the coordinates of three points — vertices of a triangle which contains all n points and which area doesn't exceed 4S.
Coordinates of every triangle's vertex should be printed on a separate line, every coordinate pair should be separated by a single space. Coordinates should be an integers not exceeding 109 by absolute value.
It is guaranteed that there is at least one desired triangle. If there is more than one answer, print any of them.
Example
4 1
0 0
1 0
0 1
1 1
-1 0
2 0
0 2
题意:给定N个点,保证最大三角形面积不超过S,现在让你找一个面积不超过4*S的三角形,使之覆盖所有点。
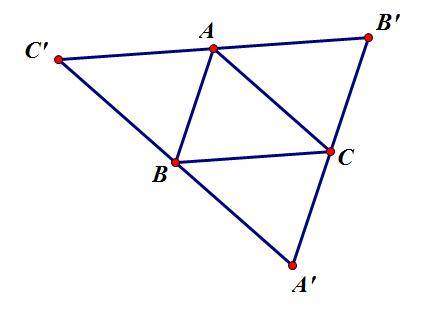
思路:找到最大三角形X,然后按照平行四边形的样子,对称出3个三角形。即可覆盖所有点,否则可以反证X的面积不是最大。
所以按照上一题一样,先求凸包,然后求最大三角形的坐标,然后对称。 如图:
#include<bits/stdc++.h> #define rep(i,a,b) for(int i=a;i<=b;i++) #define ll long long #define RC rotating_calipers using namespace std; const int maxn=100010; struct point{ ll x,y; point(ll x=0,ll y=0):x(x),y(y){} bool operator <(const point &c) const { return x<c.x||(x==c.x&&y<c.y);} point operator -(const point &c)const { return point(x-c.x,y-c.y);} }; ll det(point A,point B){ return A.x*B.y-A.y*B.x;} ll det(point O,point A,point B){ return det(A-O,B-O);} point a[maxn],ch[maxn],A,B,C; void convexhull(int n,int &top) { sort(a+1,a+n+1); top=0; for(int i=1;i<=n;i++){ while(top>1&&det(ch[top-1],ch[top],a[i])<=0) top--; ch[++top]=a[i]; } int ttop=top; for(int i=n-1;i>=1;i--){ while(top>ttop&&det(ch[top-1],ch[top],a[i])<=0) top--; ch[++top]=a[i]; } } void rotating_calipers(point p[],int top) { ll ans=0; int now; rep(i,1,top-2){ int now=i+2; rep(j,i+1,top-1){ while(now<=top&&abs(det(p[i],p[j],p[now]))<abs(det(p[i],p[j],p[now+1]))){ now++; } ll tmp=abs(det(p[i],p[j],p[now])); if(tmp>ans) ans=tmp,A=p[i],B=p[j],C=p[now]; } } } int main() { int N; ll S; scanf("%d%I64d",&N,&S); for(int i=1;i<=N;i++) scanf("%I64d%I64d",&a[i].x,&a[i].y); int top; convexhull(N,top); RC(ch,top-1); printf("%I64d %I64d ",A.x+B.x-C.x,A.y+B.y-C.y); printf("%I64d %I64d ",A.x+C.x-B.x,A.y+C.y-B.y); printf("%I64d %I64d ",B.x+C.x-A.x,B.y+C.y-A.y); return 0; }