之前在给最大流题目分类,后来整理不知道怎么继续http://www.cnblogs.com/hua-dong/p/7834447.html毕竟最大流里面东西也多。重新整理一下已经理解的俩个类型。
【最小权闭合子图】
【结论】:最大权闭合子图=收益-最小割=收益-最大流,以下是自己YY的最小值比较法来证明。
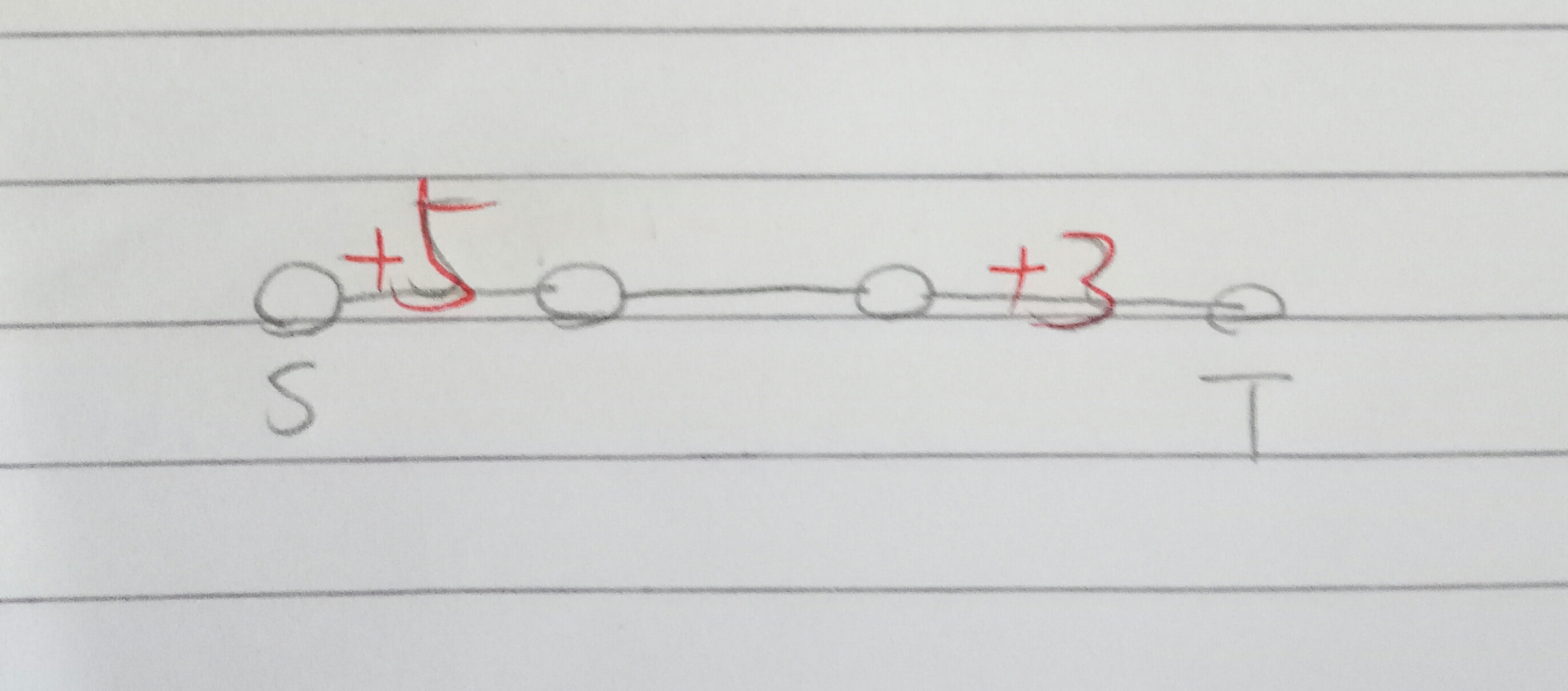
首先考虑一下如何用最大流来比较两个数a和b的大小;
设a=5;b=3;
如下图,最大流跑一趟,答案是min=b=3 ;不难知道割总是发生再最小值处,就:3-T这条边是割
那么,和闭合权值有什么关系呢?看下图,我们如何用上面的思路来得到节目的收益减去人员的工资来得到收益。
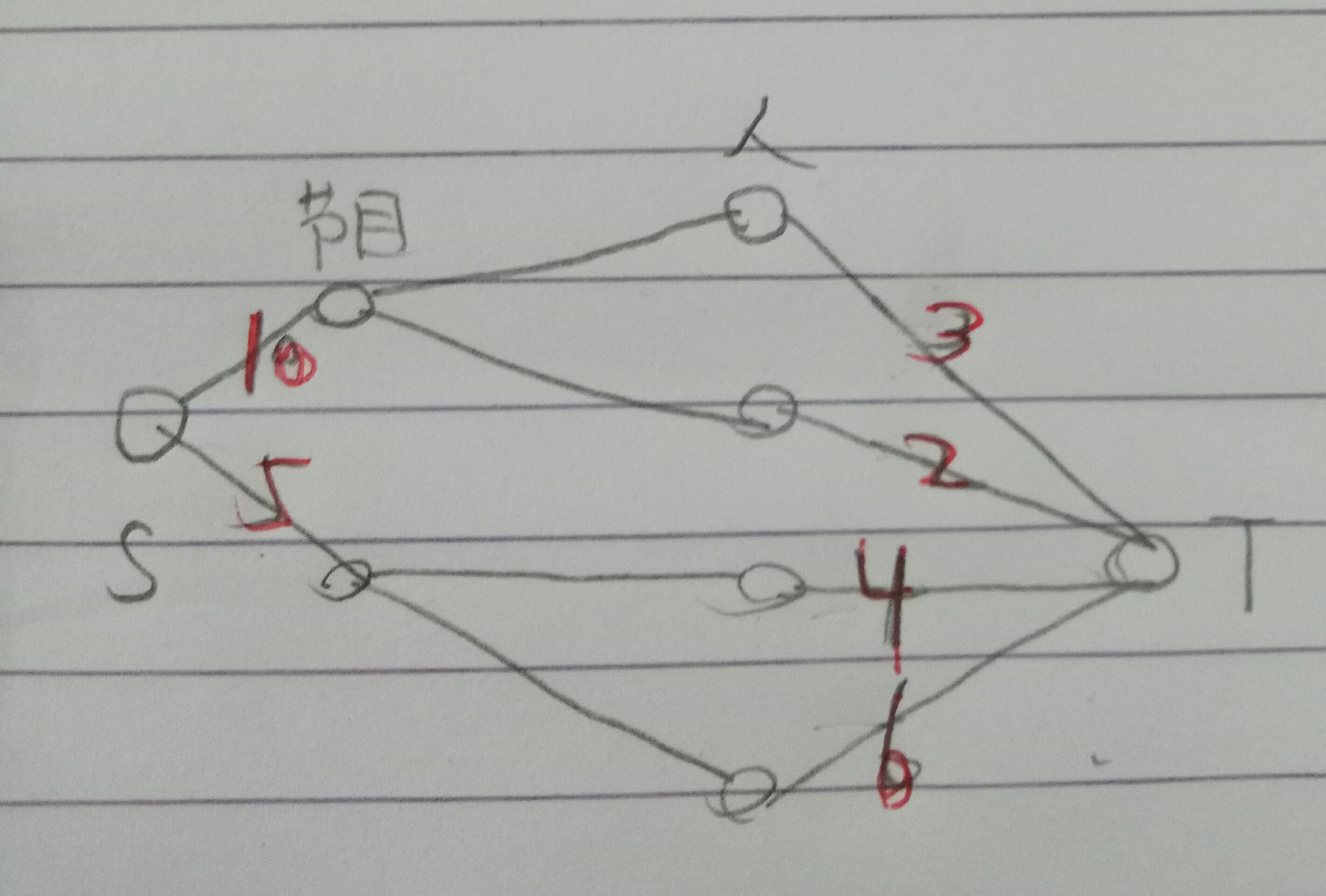
它跑一趟最大流得到了是max_flow =(2+3)+5;即割是3和2和5的这三条边。节目代表的数字(10和5)是收益,人代表的数字(3,2,4,6)是付出。则第一个节目,我们的净收益是10-(2+3)=5;第二个节目收益是5-5=0;
这表示第一个节目有盈余5,第二个节目无盈余,也补亏损。可以肯定,每个节目收益最坏的情况不会为小于0,即出现亏损。
节目和人的情况无非两种:
如果左边的值大于右边,那么右边是割,收益减去割(付出),有盈余;
如果左边的值小于右边,那么左边是割,收益减去割(本身),为0;
这是再没有交叉的情况下,那么有交叉的时候。
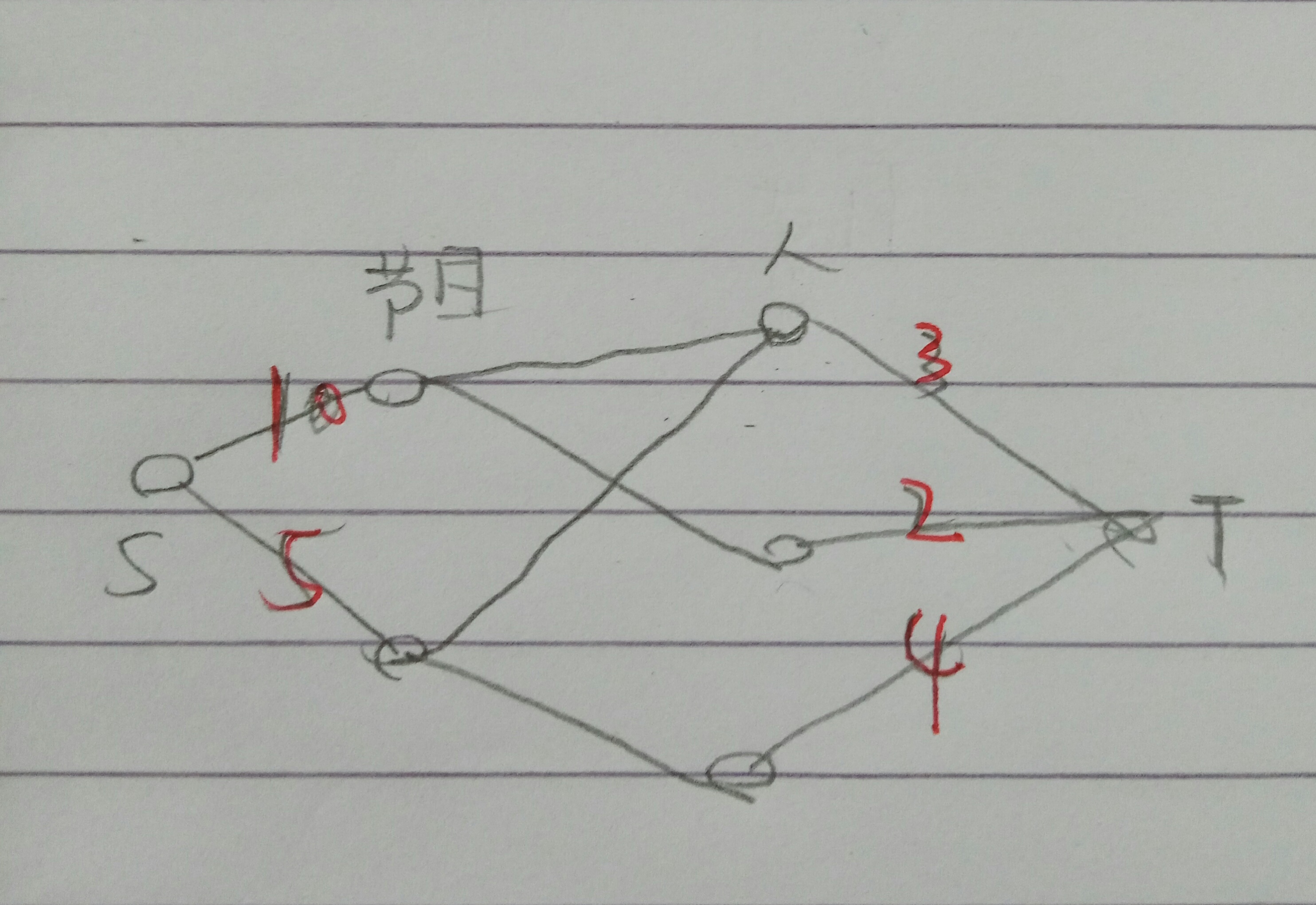
道理是一样是的,求最大流的过程如下:
先找增广路,路过了节目1 S-节目1(+10)—人(-2,-3)—T,得到最大流5,但是此时2和3变成了0;
再找增广路,路过了节目2 S-节目2(+5)—人(-0,-4)—T,得到最大流1,此时4变成了0;
找不到增广路,结束。
由此,我们用比较最小值的思路证明了最大权闭合权值=收益-最小割=收益-最大流
(题目:最大权闭合子图)


#include<cstdio> #include<cstdlib> #include<cstring> #include<cmath> #include<iostream> using namespace std; const int maxn=50000; const int inf=1000000000; int Laxt[maxn],Next[maxn],To[maxn],Cap[maxn],cnt=1; int dis[maxn],vd[maxn],S,T; void add(int u,int v,int c) { Next[++cnt]=Laxt[u]; Laxt[u]=cnt; To[cnt]=v; Cap[cnt]=c; Next[++cnt]=Laxt[v]; Laxt[v]=cnt; To[cnt]=u; Cap[cnt]=0; } int sap(int u,int flow) { if(u==T||flow==0) return flow; int delta=0,temp; for(int i=Laxt[u];i;i=Next[i]){ int v=To[i]; if(dis[v]+1==dis[u]&&Cap[i]>0){ temp=sap(v,min(flow-delta,Cap[i])); delta+=temp; Cap[i]-=temp; Cap[i^1]+=temp; if(dis[1]>=T||delta==flow) return delta; } } vd[dis[u]]--; if(vd[dis[u]]==0) dis[S]=T; vd[++dis[u]]++; return delta; } int main() { int n,m,i,j,u,v,ans=0,num=0,x; scanf("%d%d",&n,&m); S=1;T=2+n+m; for(i=1;i<=m;i++){ scanf("%d",&x); add(S,i+1,x); } for(i=1;i<=n;i++){ scanf("%d",&x); num+=x; add(m+1+i,T,x); scanf("%d",&v); for(j=1;j<=v;j++){ scanf("%d",&u); add(u+1,m+1+i,inf); } } while(dis[S]<T) ans+=sap(S,inf); printf("%d ",num-ans); return 0; }
【最小路径覆盖】
【定义】:给定一个有向无环图,用最少的路径数量去保证所有点都被覆盖住。
【结论】:最小路径覆盖的结果等于N-最大二分匹配。
一下是用‘度’来证明,这个证明网上到处都有:
【先说有向图如何联系上了二分图】
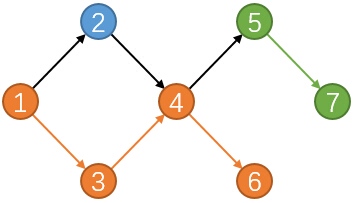
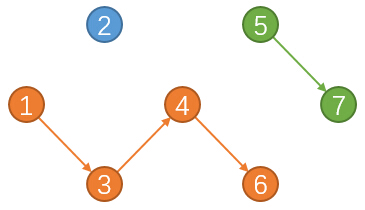
在这个例子中,我们选择的三条路径都被染上了颜色。
黑色的边去掉,注意的是每个点的出入度数量。
对于一条路径,起点的入度为0,终点的出度为0,中间节点的出入度都为1。
每一个点最多只能有1个后继,同时每一个点最多只能有1个前驱。
假如我们选择了一条边(u,v),也就等价于把前驱u和后继v匹配上了。这样前驱u和后继v就不能和其他节点匹配。
将每一个点拆分成2个,分别表示它作为前驱节点和后继节点。将所有的前驱节点作为A部,所有后继节点作为B部。
接下来进行连边,若原图中存在一条边(u,v),则连接A部的u和B部的v。
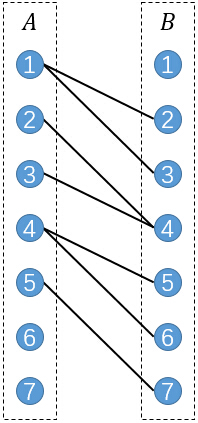
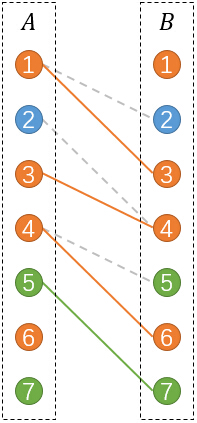
其中实线表示被选中的匹配,虚线表示未被选中的。
发现,和原图刚好有着对应的关系。未被选中的匹配也正好对应了原图中我们没有选择的黑色边。
原理很简单。我们进行的匹配是前驱和后继的匹配。假如存在选中的匹配(i,j)和(j,k)。则表示原图中存在一条路径(i,j,k)。
比如例子中的匹配(1,3),(3,4),(4,6)就对应了原图中的路径(1,3,4,6)。
这样在匹配结束的时候,我们就可以直接通过匹配的情况来确定选中的路径。
【如何保证这样就能得到最小的路径覆盖】?
路径的起点入度为0,
如果一个点是路径起点的话,它在B部的节点一定是没有匹配上的。
经过最大匹配算法后,B部剩下没有被匹配的点一定是最少的,也就对应了最小需要的路径数。
所以最小路径覆盖的结果才是N-最大匹配数。
【如果两条路径可以有交点】
先用floyd闭包传递。
(这个思路可以想到HDU3488如何建图)


#include<cstdio> #include<cstdlib> #include<cstring> #include<cmath> #include<iostream> using namespace std; const int maxn=50000; const int inf=1000000000; int Laxt[maxn],Next[maxn],To[maxn],Cap[maxn],cnt=1; int dis[maxn],vd[maxn],S,T; void add(int u,int v,int c) { Next[++cnt]=Laxt[u]; Laxt[u]=cnt; To[cnt]=v; Cap[cnt]=c; Next[++cnt]=Laxt[v]; Laxt[v]=cnt; To[cnt]=u; Cap[cnt]=0; } int sap(int u,int flow) { if(u==T||flow==0) return flow; int delta=0,temp; for(int i=Laxt[u];i;i=Next[i]){ int v=To[i]; if(dis[v]+1==dis[u]&&Cap[i]>0){ temp=sap(v,min(flow-delta,Cap[i])); delta+=temp; Cap[i]-=temp; Cap[i^1]+=temp; if(dis[1]>=T||delta==flow) return delta; } } vd[dis[u]]--; if(vd[dis[u]]==0) dis[S]=T; vd[++dis[u]]++; return delta; } int main() { int n,m,i,u,v,ans=0; scanf("%d%d",&n,&m); S=1;T=2+n+n; for(i=1;i<=m;i++){ scanf("%d%d",&u,&v); add(u+1,v+n+1,1); } for(i=1+1;i<=1+n;i++) add(S,i,1); for(i=n+1+1;i<=n+1+n;i++) add(i,T,1); while(dis[S]<T) ans+=sap(S,inf); printf("%d ",n-ans); return 0; }