连通性·四
描述
小Hi和小Ho从约翰家回到学校时,网络所的老师又找到了小Hi和小Ho。
老师告诉小Hi和小Ho:之前的分组出了点问题,当服务器(上次是连接)发生宕机的时候,在同一组的服务器有可能连接不上,所以他们希望重新进行一次分组。这一次老师希望对连接进行分组,并把一个组内的所有连接关联的服务器也视为这个组内的服务器(注意一个服务器可能属于多个组)。
这一次的条件是对于同一个组满足:当组内任意一个服务器宕机之后,不会影响组内其他服务器的连通性。在满足以上条件下,每个组内的边数量越多越好。
比如下面这个例子,一共有6个服务器和7条连接:

其中包含3个组,分别为{(1,2),(2,3),(3,1)},{(4,5),(5,6),(4,6)},{(3,4)}。对{(1,2),(2,3),(3,1)}而言,和该组边相关联的有{1,2,3}三个服务器:当1宕机后,仍然有2-3可以连接2和3;当2宕机后,仍然有1-3可以连接1和3;当3宕机后,仍然有1-2可以连接1和2。
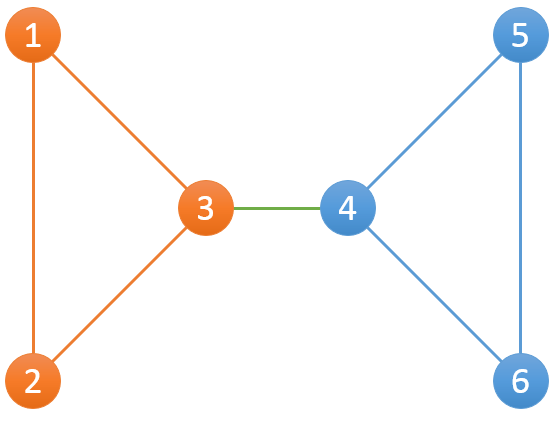
老师把整个网络的情况告诉了小Hi和小Ho,希望小Hi和小Ho统计一下一共有多少个分组。
输入
第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000
第2..M+1行:2个正整数,u,v。第i+1行表示存在一条边(u,v),编号为i,连接了u,v两台服务器。1≤u<v≤N
保证输入所有点之间至少有一条连通路径。
输出
第1行:1个整数,表示该网络的连接组数。
第2行:M个整数,第i个数表示第i条连接所属组内,编号最小的连接的编号。比如分为{(1,2)[1],(2,3)[3],(3,1)[2]},{(4,5)[5],(5,6)[7],(4,6)[6]},{(3,4)[4]},方括号内表示编号,则输出{1,1,1,4,5,5,5}。
- 样例输入
-
6 7 1 2 1 3 2 3 3 4 4 5 4 6 5 6
- 样例输出
-
3 1 1 1 4 5 5 5
第一次写存边的题,还是有些小疑惑,主要还是这种存边方式不太正宗。存两个点比较普遍。
QwQ,今天看数论看哭了,然后才回来补这道题。
#include<cstdio> #include<cstdlib> #include<cstring> #include<algorithm> #include<iostream> using namespace std; const int maxn=200010; int Laxt[maxn],Next[maxn],To[maxn],ID[maxn],cnt; int low[maxn],dfn[maxn],times; int q[maxn],top,scc[maxn],Min[maxn],scc_cnt; void add(int u,int v,int d) { Next[++cnt]=Laxt[u]; Laxt[u]=cnt; To[cnt]=v; ID[cnt]=d; } void tarjan(int u,int pre) { dfn[u]=low[u]=++times; for(int i=Laxt[u];i;i=Next[i]){ int v=To[i]; int id=ID[i]; if(v==pre) continue; if(!dfn[v]){ q[++top]=id; tarjan(v,u); low[u]=min(low[u],low[v]); if(dfn[u]<=low[v]){ scc_cnt++; while(true){ int tmp=q[top--]; scc[tmp]=scc_cnt; Min[scc_cnt]=Min[scc_cnt]==0?tmp:min(Min[scc_cnt],tmp); if(tmp==id) break; } } } else if(dfn[v]<dfn[u]){//回边,思考为什么加这个 low[u]=min(low[u],dfn[v]); q[++top]=id; } } } int main() { int i,j,n,m,u,v; scanf("%d%d",&n,&m); for(i=1;i<=m;i++){ scanf("%d%d",&u,&v); add(u,v,i); add(v,u,i); } tarjan(1,-1); printf("%d ",scc_cnt); for(i=1;i<=m;i++) printf("%d ",Min[scc[i]]); return 0; }