At regular competition Vladik and Valera won a and b candies respectively. Vladik offered 1 his candy to Valera. After that Valera gave Vladik 2 his candies, so that no one thought that he was less generous. Vladik for same reason gave 3 candies to Valera in next turn.
More formally, the guys take turns giving each other one candy more than they received in the previous turn.
This continued until the moment when one of them couldn’t give the right amount of candy. Candies, which guys got from each other, they don’t consider as their own. You need to know, who is the first who can’t give the right amount of candy.
Single line of input data contains two space-separated integers a, b (1 ≤ a, b ≤ 109) — number of Vladik and Valera candies respectively.
Pring a single line "Vladik’’ in case, if Vladik first who can’t give right amount of candy, or "Valera’’ otherwise.
1 1
Valera
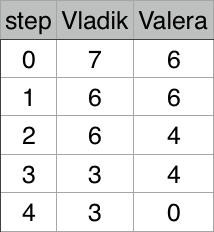
7 6
Vladik
Illustration for first test case:
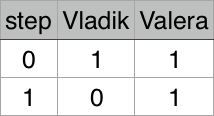
Illustration for second test case:
题意:给你两个数 a,b 按照 1 2 3 4 ...i a b轮流减少相应的i值 若a先减少到0 输出Vladik 反之输出Valera
题解:水
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<cstring> 5 #include<queue> 6 #include<map> 7 #include<vector> 8 #include<algorithm> 9 #define ll __int64 10 using namespace std; 11 int main() 12 { 13 int a,b; 14 scanf("%d %d",&a,&b); 15 int s=0,d=0; 16 s=sqrt(a); 17 for(int i=sqrt(b);;i--) 18 { 19 if(i*(i+1)<=b) 20 { 21 d=i; 22 break; 23 } 24 } 25 // cout<<s<<" "<<d<<endl; 26 if(s<=d) 27 printf("Vladik "); 28 else 29 printf("Valera "); 30 return 0; 31 }
Vladik had started reading a complicated book about algorithms containing n pages. To improve understanding of what is written, his friends advised him to read pages in some order given by permutation P = [p1, p2, ..., pn], where pi denotes the number of page that should be read i-th in turn.
Sometimes Vladik’s mom sorted some subsegment of permutation P from position l to position r inclusive, because she loves the order. For every of such sorting Vladik knows number x — what index of page in permutation he should read. He is wondered if the page, which he will read after sorting, has changed. In other words, has px changed? After every sorting Vladik return permutation to initial state, so you can assume that each sorting is independent from each other.
First line contains two space-separated integers n, m (1 ≤ n, m ≤ 104) — length of permutation and number of times Vladik's mom sorted some subsegment of the book.
Second line contains n space-separated integers p1, p2, ..., pn (1 ≤ pi ≤ n) — permutation P. Note that elements in permutation are distinct.
Each of the next m lines contains three space-separated integers li, ri, xi (1 ≤ li ≤ xi ≤ ri ≤ n) — left and right borders of sorted subsegment in i-th sorting and position that is interesting to Vladik.
For each mom’s sorting on it’s own line print "Yes", if page which is interesting to Vladik hasn't changed, or "No" otherwise.
5 5
5 4 3 2 1
1 5 3
1 3 1
2 4 3
4 4 4
2 5 3
Yes
No
Yes
Yes
No
6 5
1 4 3 2 5 6
2 4 3
1 6 2
4 5 4
1 3 3
2 6 3
Yes
No
Yes
No
Yes
Explanation of first test case:
- [1, 2, 3, 4, 5] — permutation after sorting, 3-rd element hasn’t changed, so answer is "Yes".
- [3, 4, 5, 2, 1] — permutation after sorting, 1-st element has changed, so answer is "No".
- [5, 2, 3, 4, 1] — permutation after sorting, 3-rd element hasn’t changed, so answer is "Yes".
- [5, 4, 3, 2, 1] — permutation after sorting, 4-th element hasn’t changed, so answer is "Yes".
- [5, 1, 2, 3, 4] — permutation after sorting, 3-rd element has changed, so answer is "No".
题意:给你一个长度为n的序列p m个查询 将[l,r] 升序排列 判断px是否改变 如果没有改变输出Yes 否则输出No
题解:遍历判断当前区间 小于px的数的数量;
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<cstring> 5 #include<queue> 6 #include<map> 7 #include<vector> 8 #include<algorithm> 9 #define ll __int64 10 using namespace std; 11 int n,m; 12 int a[10005]; 13 int main(){ 14 scanf("%d %d",&n,&m); 15 for(int i=1;i<=n;i++) 16 scanf("%d",&a[i]); 17 int l,r,x; 18 for(int i=1;i<=m;i++){ 19 scanf("%d %d %d",&l,&r,&x); 20 int jishu=0; 21 for(int j=l;j<=r;j++) 22 { 23 if(a[j]<=a[x]) 24 jishu++; 25 } 26 if(jishu==(x-l+1)) 27 printf("Yes "); 28 else 29 printf("No "); 30 } 31 return 0; 32 }
Vladik often travels by trains. He remembered some of his trips especially well and I would like to tell you about one of these trips:
Vladik is at initial train station, and now n people (including Vladik) want to get on the train. They are already lined up in some order, and for each of them the city code ai is known (the code of the city in which they are going to).
Train chief selects some number of disjoint segments of the original sequence of people (covering entire sequence by segments is not necessary). People who are in the same segment will be in the same train carriage. The segments are selected in such way that if at least one person travels to the city x, then all people who are going to city x should be in the same railway carriage. This means that they can’t belong to different segments. Note, that all people who travel to the city x, either go to it and in the same railway carriage, or do not go anywhere at all.
Comfort of a train trip with people on segment from position l to position r is equal to XOR of all distinct codes of cities for people on the segment from position l to position r. XOR operation also known as exclusive OR.
Total comfort of a train trip is equal to sum of comfort for each segment.
Help Vladik to know maximal possible total comfort.
First line contains single integer n (1 ≤ n ≤ 5000) — number of people.
Second line contains n space-separated integers a1, a2, ..., an (0 ≤ ai ≤ 5000), where ai denotes code of the city to which i-th person is going.
The output should contain a single integer — maximal possible total comfort.
6
4 4 2 5 2 3
14
9
5 1 3 1 5 2 4 2 5
9
In the first test case best partition into segments is: [4, 4] [2, 5, 2] [3], answer is calculated as follows: 4 + (2 xor 5) + 3 = 4 + 7 + 3 = 14
In the second test case best partition into segments is: 5 1 [3] 1 5 [2, 4, 2] 5, answer calculated as follows: 3 + (2 xor 4) = 3 + 6 = 9.
题意:给出n,然后n个数,要你选择一些不相交的区间,使得这些区间中出现的数字的异或的和最大,区间有这样的限制,对于区间的任何数,其余相同的数都要在这个区间,否者这个区间就是不合法的。
题解:求出每个数出现的最左端和最右端,定义dp[i]为1到i这个区间所能选出的最大值,然后枚举右端点,找合法的左端点即可
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<cstring> 5 #include<queue> 6 #include<map> 7 #include<vector> 8 #include<algorithm> 9 #define ll __int64 10 using namespace std; 11 int n; 12 ll a[5005]; 13 int l[5005],r[5005]; 14 ll we[5005][5005]; 15 ll dp[5005]; 16 int mp[5005]; 17 int main() 18 { 19 scanf("%d",&n); 20 for(int i=1;i<=n;i++){ 21 scanf("%d",&a[i]); 22 l[a[i]]=n; 23 r[a[i]]=1; 24 } 25 for(int i=1;i<=n;i++){ 26 l[a[i]]=min(l[a[i]],i); 27 r[a[i]]=max(r[a[i]],i); 28 } 29 for(int i=1;i<=n;i++){ 30 memset(mp,0,sizeof(mp)); 31 we[i][i]=a[i]; 32 mp[a[i]]=1; 33 int sum=a[i]; 34 for(int j=i+1;j<=n;j++){ 35 if(mp[a[j]]==0){ 36 sum=sum^a[j]; 37 mp[a[j]]=1; 38 } 39 we[i][j]=sum; 40 } 41 } 42 dp[0]=0; 43 for(int i=1;i<=n;i++){ 44 if(r[a[i]]==i){ 45 int L=l[a[i]]; 46 int what=1; 47 for(int j=l[a[i]]+1;j<r[a[i]];j++){ 48 if(r[a[j]]>i){ 49 what=0; 50 break; 51 } 52 L=min(L,l[a[j]]); 53 } 54 if(what==1) 55 dp[i]=max(dp[i-1],dp[L-1]+we[L][i]); 56 else 57 dp[i]=dp[i-1]; 58 } 59 else 60 dp[i]=dp[i-1]; 61 } 62 printf("%I64d ",dp[n]); 63 return 0; 64 }