Codeforces Round #407 (Div. 2)A B C 水 暴力 最大子序列和

A. Anastasia and pebbles

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Anastasia loves going for a walk in Central Uzhlyandian Park. But she became uninterested in simple walking, so she began to collect Uzhlyandian pebbles. At first, she decided to collect all the pebbles she could find in the park.

She has only two pockets. She can put at most k pebbles in each pocket at the same time. There are n different pebble types in the park, and there are w_i pebbles of the i-th type. Anastasia is very responsible, so she never mixes pebbles of different types in same pocket. However, she can put different kinds of pebbles in different pockets at the same time. Unfortunately, she can't spend all her time collecting pebbles, so she can collect pebbles from the park only once a day.

Help her to find the minimum number of days needed to collect all the pebbles of Uzhlyandian Central Park, taking into consideration that Anastasia can't place pebbles of different types in same pocket.

Input

The first line contains two integers n and k (1 ≤ n ≤ 10⁵, 1 ≤ k ≤ 10⁹) — the number of different pebble types and number of pebbles Anastasia can place in one pocket.

The second line contains n integers w₁, w₂, ..., w_n (1 ≤ w_i ≤ 10⁴) — number of pebbles of each type.

Output

The only line of output contains one integer — the minimum number of days Anastasia needs to collect all the pebbles.

Examples

Input

3 2
2 3 4

Output

3

Input

5 4
3 1 8 9 7

Output

5

Note

In the first sample case, Anastasia can collect all pebbles of the first type on the first day, of second type — on the second day, and of third type — on the third day.

Optimal sequence of actions in the second sample case:

• In the first day Anastasia collects 8 pebbles of the third type.
• In the second day she collects 8 pebbles of the fourth type.
• In the third day she collects 3 pebbles of the first type and 1 pebble of the fourth type.
• In the fourth day she collects 7 pebbles of the fifth type.
• In the fifth day she collects 1 pebble of the second type.

题意：n个东西 每次有两个容量为k的容器 给你n个东西的大小  问你需要装几次可以装走所有的物品  每次同一个容器中只能放置一种东西

题解：水

#include<bits/stdc++.h>
using namespace std;
int n,k;
int exm;
int main()
{
    scanf("%d %d",&n,&k);
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&exm);
        ans=ans+exm/k;
        if(exm%k)
            ans++;
    }
    int re=0;
    re=ans/2;
    if(ans%2)
        re++;
    printf("%d
",re);
    return 0;
}

B. Masha and geometric depression

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Masha really loves algebra. On the last lesson, her strict teacher Dvastan gave she new exercise.

You are given geometric progression b defined by two integers b₁ and q. Remind that a geometric progression is a sequence of integers b₁, b₂, b₃, ..., where for each i > 1 the respective term satisfies the condition b_i = b_i - 1·q, where q is called the common ratio of the progression. Progressions in Uzhlyandia are unusual: both b₁ and q can equal 0. Also, Dvastan gave Masha m "bad" integers a₁, a₂, ..., a_m, and an integer l.

Masha writes all progression terms one by one onto the board (including repetitive) while condition |b_i| ≤ l is satisfied (|x| means absolute value of x). There is an exception: if a term equals one of the "bad" integers, Masha skips it (doesn't write onto the board) and moves forward to the next term.

But the lesson is going to end soon, so Masha has to calculate how many integers will be written on the board. In order not to get into depression, Masha asked you for help: help her calculate how many numbers she will write, or print "inf" in case she needs to write infinitely many integers.

Input

The first line of input contains four integers b₁, q, l, m (-10⁹ ≤ b₁, q ≤ 10⁹, 1 ≤ l ≤ 10⁹, 1 ≤ m ≤ 10⁵) — the initial term and the common ratio of progression, absolute value of maximal number that can be written on the board and the number of "bad" integers, respectively.

The second line contains m distinct integers a₁, a₂, ..., a_m (-10⁹ ≤ a_i ≤ 10⁹) — numbers that will never be written on the board.

Output

Print the only integer, meaning the number of progression terms that will be written on the board if it is finite, or "inf" (without quotes) otherwise.

Examples

Input

3 2 30 4
6 14 25 48

Output

3

Input

123 1 2143435 4
123 11 -5453 141245

Output

0

Input

123 1 2143435 4
54343 -13 6 124

Output

inf

Note

In the first sample case, Masha will write integers 3, 12, 24. Progression term 6 will be skipped because it is a "bad" integer. Terms bigger than 24 won't be written because they exceed l by absolute value.

In the second case, Masha won't write any number because all terms are equal 123 and this is a "bad" integer.

In the third case, Masha will write infinitely integers 123.

题意：给你一个等比数列的初项 公比  数字的上界 现在写出满足的项 有m个不能出现的数字 问能写出多少项

题解：暴力

#include<bits/stdc++.h>
#define ll __int64
using namespace std;
ll b1,q,l,m;
ll exm;
map<ll,int>mp;
ll ans=0;
int main()
{
    scanf("%I64d %I64d %I64d %I64d",&b1,&q,&l,&m);
    for(ll i=1;i<=m;i++)
    {
        scanf("%I64d",&exm);
        mp[exm]=1;
    }
    for(int i=1;i<=1000;i++)
        ans=0;
    for(int i=0;i<501;i++)
    {
        if(abs(b1)>l) break;
        if(mp[b1]!=1) ans++;
        b1*=q;
    }
    if(ans>100)
        printf("inf
");
    else
        printf("%I64d
",ans);
    return 0;
}

C. Functions again

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Something happened in Uzhlyandia again... There are riots on the streets... Famous Uzhlyandian superheroes Shean the Sheep and Stas the Giraffe were called in order to save the situation. Upon the arriving, they found that citizens are worried about maximum values of the Main Uzhlyandian Function f, which is defined as follows:

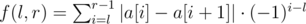
In the above formula, 1 ≤ l < r ≤ n must hold, where n is the size of the Main Uzhlyandian Array a, and |x| means absolute value of x. But the heroes skipped their math lessons in school, so they asked you for help. Help them calculate the maximum value of f among all possible values of l and r for the given array a.

Input

The first line contains single integer n (2 ≤ n ≤ 10⁵) — the size of the array a.

The second line contains n integers a₁, a₂, ..., a_n (-10⁹ ≤ a_i ≤ 10⁹) — the array elements.

Output

Print the only integer — the maximum value of f.

Examples

Input

5
1 4 2 3 1

Output

3

Input

4
1 5 4 7

Output

6

Note

In the first sample case, the optimal value of f is reached on intervals [1, 2] and [2, 5].

In the second case maximal value of f is reachable only on the whole array.

题意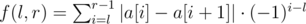：   给你一个长度为n的数列 对于这个数列输出最大的f(l,r)

题解：处理出每一项绝对值 求两遍最大子序列和

#include<bits/stdc++.h>
#define ll __int64
using namespace std;
int n;
ll a[100005];
ll b[100005];
ll c[100005];
int main()
{
    scanf("%d",&n);
    for(int i=1; i<=n; i++)
        scanf("%I64d",&a[i]);
    ll exm=0;
    for(int i=1; i<n; i++)
    {
        exm=a[i]-a[i+1];
        if(exm<0)
            exm=-exm;
        if(i%2==1)
        {
            b[i]=exm;
            c[i]=-exm;
        }
        else
        {
            b[i]=-exm;
            c[i]=exm;
        }
    }
    ll sum=0;
    ll maxn1=-1e15,maxn2=-1e15;
    for(int i=1; i<n; i++)
    {
        sum+=b[i];
        if(sum>maxn1)
        {
            maxn1=sum;
        }
        else if(sum<0)
        {
            sum=0;
            if(i%2==1)
                i--;
        }
    }
    sum=0;
    for(int i=2; i<n; i++)
    {
        sum+=c[i];
        if(sum>maxn2)
        {
            maxn2=sum;
        }
        else if(sum<0)
        {
            sum=0;
            if(i%2==0)
                i--;
        }
    }
    cout<<max(maxn1,maxn2)<<endl;
    return 0;
}