On her way to programming school tiger Dasha faced her first test — a huge staircase!
The steps were numbered from one to infinity. As we know, tigers are very fond of all striped things, it is possible that it has something to do with their color. So on some interval of her way she calculated two values — the number of steps with even and odd numbers.
You need to check whether there is an interval of steps from the l-th to the r-th (1 ≤ l ≤ r), for which values that Dasha has found are correct.
In the only line you are given two integers a, b (0 ≤ a, b ≤ 100) — the number of even and odd steps, accordingly.
In the only line print "YES", if the interval of steps described above exists, and "NO" otherwise.
2 3
YES
3 1
NO
In the first example one of suitable intervals is from 1 to 5. The interval contains two even steps — 2 and 4, and three odd: 1, 3 and 5.
题意：判断是否能够走a个偶数步 b个奇数步
题解：水
1 #include <iostream> 2 #include <cstdio> 3 #include <cstdlib> 4 #include <cstring> 5 #include <algorithm> 6 #include <stack> 7 #include <queue> 8 #include <cmath> 9 #include <map> 10 #define ll __int64 11 #define mod 1000000007 12 #define dazhi 2147483647 13 using namespace std; 14 int a,b; 15 int main() 16 { 17 scanf("%d %d",&a,&b); 18 if(a==0&&b==0) 19 { 20 printf("NO "); 21 return 0; 22 } 23 if(a==b||a+1==b||b+1==a) 24 printf("YES "); 25 else 26 printf("NO "); 27 return 0; 28 }
Running with barriers on the circle track is very popular in the country where Dasha lives, so no wonder that on her way to classes she saw the following situation:
The track is the circle with length L, in distinct points of which there are n barriers. Athlete always run the track in counterclockwise direction if you look on him from above. All barriers are located at integer distance from each other along the track.
Her friends the parrot Kefa and the leopard Sasha participated in competitions and each of them ran one lap. Each of the friends started from some integral point on the track. Both friends wrote the distance from their start along the track to each of the n barriers. Thus, each of them wrote n integers in the ascending order, each of them was between 0 and L - 1, inclusively.
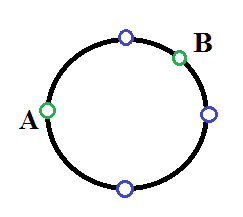Consider an example. Let L = 8, blue points are barriers, and green points are Kefa's start (A) and Sasha's start (B). Then Kefa writes down the sequence [2, 4, 6], and Sasha writes down [1, 5, 7]. There are several tracks in the country, all of them have same length and same number of barriers, but the positions of the barriers can differ among different tracks. Now Dasha is interested if it is possible that Kefa and Sasha ran the same track or they participated on different tracks.
Write the program which will check that Kefa's and Sasha's tracks coincide (it means that one can be obtained from the other by changing the start position). Note that they always run the track in one direction — counterclockwise, if you look on a track from above.
The first line contains two integers n and L (1 ≤ n ≤ 50, n ≤ L ≤ 100) — the number of barriers on a track and its length.
The second line contains n distinct integers in the ascending order — the distance from Kefa's start to each barrier in the order of its appearance. All integers are in the range from 0 to L - 1 inclusively.
The second line contains n distinct integers in the ascending order — the distance from Sasha's start to each barrier in the order of its overcoming. All integers are in the range from 0 to L - 1 inclusively.
Print "YES" (without quotes), if Kefa and Sasha ran the coinciding tracks (it means that the position of all barriers coincides, if they start running from the same points on the track). Otherwise print "NO" (without quotes).
3 8
2 4 6
1 5 7
YES
4 9
2 3 5 8
0 1 3 6
YES
2 4
1 3
1 2
NO
The first test is analyzed in the statement.
题意：长度为了l的环 有n个观测点 现在AB两个人描述自己逆时针距离各个观测点的距离 判断是否满足实际
题解：暴力
1 #include <iostream> 2 #include <cstdio> 3 #include <cstdlib> 4 #include <cstring> 5 #include <algorithm> 6 #include <stack> 7 #include <queue> 8 #include <cmath> 9 #include <map> 10 #define ll __int64 11 #define mod 1000000007 12 #define dazhi 2147483647 13 using namespace std; 14 int n,l; 15 int a[105]; 16 int b[105]; 17 map<int,int >mp; 18 int main() 19 { 20 scanf("%d %d",&n,&l); 21 for(int i=0;i<n;i++) 22 scanf("%d",&a[i]); 23 for(int i=0;i<n;i++) 24 scanf("%d",&b[i]); 25 int jishu=0; 26 for(int i=0;i<l;i++) 27 { 28 for(int j=0;j<l;j++) 29 { 30 jishu=0; 31 mp.clear(); 32 for(int k=0;k<n;k++) 33 mp[(i+a[k])%l]=1; 34 for(int k=0;k<n;k++) 35 if(mp[(j+b[k])%l]) 36 jishu++; 37 if(jishu==n) 38 { 39 printf("YES "); 40 return 0; 41 } 42 } 43 } 44 printf("NO "); 45 return 0; 46 }
After overcoming the stairs Dasha came to classes. She needed to write a password to begin her classes. The password is a string of length n which satisfies the following requirements:
- There is at least one digit in the string,
- There is at least one lowercase (small) letter of the Latin alphabet in the string,
- There is at least one of three listed symbols in the string: '#', '*', '&'.
Considering that these are programming classes it is not easy to write the password.
For each character of the password we have a fixed string of length m, on each of these n strings there is a pointer on some character. The i-th character displayed on the screen is the pointed character in the i-th string. Initially, all pointers are on characters with indexes 1 in the corresponding strings (all positions are numbered starting from one).
During one operation Dasha can move a pointer in one string one character to the left or to the right. Strings are cyclic, it means that when we move the pointer which is on the character with index 1 to the left, it moves to the character with the index m, and when we move it to the right from the position m it moves to the position 1.
You need to determine the minimum number of operations necessary to make the string displayed on the screen a valid password.
The first line contains two integers n, m (3 ≤ n ≤ 50, 1 ≤ m ≤ 50) — the length of the password and the length of strings which are assigned to password symbols.
Each of the next n lines contains the string which is assigned to the i-th symbol of the password string. Its length is m, it consists of digits, lowercase English letters, and characters '#', '*' or '&'.
You have such input data that you can always get a valid password.
Print one integer — the minimum number of operations which is necessary to make the string, which is displayed on the screen, a valid password.
3 4
1**2
a3*0
c4**
1
5 5
#*&#*
*a1c&
&q2w*
#a3c#
*&#*&
3
In the first test it is necessary to move the pointer of the third string to one left to get the optimal answer.
In the second test one of possible algorithms will be:
- to move the pointer of the second symbol once to the right.
- to move the pointer of the third symbol twice to the right.
题意：给你长度为m的n个串 现在由每个串的标志位（初始为首字符）从上至下 组成密码 现在对于每个字符串执行操作 移动最小次数的标志位 使得生成密码满足题目的要求
题解：暴力
1 #include <iostream> 2 #include <cstdio> 3 #include <cstdlib> 4 #include <cstring> 5 #include <algorithm> 6 #include <stack> 7 #include <queue> 8 #include <cmath> 9 #include <map> 10 #define ll __int64 11 #define mod 1000000007 12 #define dazhi 2147483647 13 using namespace std; 14 int n,m; 15 char a[55][55]; 16 int bb[55][5]; 17 int c[55][5]; 18 int main() 19 { 20 scanf("%d %d",&n,&m); 21 //getchar(); 22 for(int i=1;i<=n;i++) 23 scanf("%s",a[i]); 24 int jishu; 25 for(int i=1;i<=n;i++) 26 for(int j=0;j<=2;j++) 27 bb[i][j]=100000; 28 for(int i=1;i<=n;i++) 29 { 30 if(a[i][0]>='0'&&a[i][0]<='9') 31 { 32 bb[i][0]=0; 33 } 34 if(a[i][0]>='a'&&a[i][0]<='z') 35 { 36 bb[i][1]=0; 37 } 38 if(a[i][0]=='*'||a[i][0]=='&'||a[i][0]=='#') 39 { 40 bb[i][2]=0; 41 } 42 jishu=1; 43 for(int j=m-1;j>0;j--) 44 { 45 if(a[i][j]>='0'&&a[i][j]<='9') 46 { 47 bb[i][0]=min(jishu,bb[i][0]); 48 } 49 if(a[i][j]>='a'&&a[i][j]<='z') 50 { 51 bb[i][1]=min(jishu,bb[i][1]); 52 } 53 if((a[i][j]=='*'||a[i][j]=='&'||a[i][j]=='#')) 54 { 55 bb[i][2]=min(jishu,bb[i][2]); 56 } 57 jishu++; 58 } 59 jishu=1; 60 for(int j=1;j<=m-1;j++) 61 { 62 if(a[i][j]>='0'&&a[i][j]<='9') 63 { 64 bb[i][0]=min(jishu,bb[i][0]); 65 } 66 if(a[i][j]>='a'&&a[i][j]<='z') 67 { 68 bb[i][1]=min(jishu,bb[i][1]); 69 } 70 if((a[i][j]=='*'||a[i][j]=='&'||a[i][j]=='#')) 71 { 72 bb[i][2]=min(jishu,bb[i][2]); 73 } 74 jishu++; 75 } 76 } 77 int ans=100000000; 78 for(int i=1;i<=n;i++) 79 { 80 for(int j=1;j<=n;j++) 81 { 82 for(int k=1;k<=n;k++) 83 { 84 if(i!=j&&j!=k&&i!=k) 85 { 86 ans=min(bb[i][0]+bb[j][1]+bb[k][2],ans); 87 } 88 } 89 } 90 } 91 printf("%d ",ans); 92 return 0; 93 }
Dasha logged into the system and began to solve problems. One of them is as follows:
Given two sequences a and b of length n each you need to write a sequence c of length n, the i-th element of which is calculated as follows: ci = bi - ai.
About sequences a and b we know that their elements are in the range from l to r. More formally, elements satisfy the following conditions: l ≤ ai ≤ r and l ≤ bi ≤ r. About sequence c we know that all its elements are distinct.
Dasha wrote a solution to that problem quickly, but checking her work on the standard test was not so easy. Due to an error in the test system only the sequence a and the compressed sequence of the sequence c were known from that test.
Let's give the definition to a compressed sequence. A compressed sequence of sequence c of length n is a sequence p of length n, so that pi equals to the number of integers which are less than or equal to ci in the sequence c. For example, for the sequence c = [250, 200, 300, 100, 50] the compressed sequence will be p = [4, 3, 5, 2, 1]. Pay attention that in c all integers are distinct. Consequently, the compressed sequence contains all integers from 1 to n inclusively.
Help Dasha to find any sequence b for which the calculated compressed sequence of sequence c is correct.
The first line contains three integers n, l, r (1 ≤ n ≤ 105, 1 ≤ l ≤ r ≤ 109) — the length of the sequence and boundaries of the segment where the elements of sequences a and b are.
The next line contains n integers a1, a2, ..., an (l ≤ ai ≤ r) — the elements of the sequence a.
The next line contains n distinct integers p1, p2, ..., pn (1 ≤ pi ≤ n) — the compressed sequence of the sequence c.
If there is no the suitable sequence b, then in the only line print "-1".
Otherwise, in the only line print n integers — the elements of any suitable sequence b.
5 1 5
1 1 1 1 1
3 1 5 4 2
3 1 5 4 2
4 2 9
3 4 8 9
3 2 1 4
2 2 2 9
6 1 5
1 1 1 1 1 1
2 3 5 4 1 6
-1
Sequence b which was found in the second sample is suitable, because calculated sequence c = [2 - 3, 2 - 4, 2 - 8, 9 - 9] = [ - 1, - 2, - 6, 0] (note that ci = bi - ai) has compressed sequence equals to p = [3, 2, 1, 4].
题意：给你ai pi 现在要求判断并输出合适的bi 使得 bi-ai 离散化之后满足pi 无法实现则输出-1
题解：二分
1 #include <iostream> 2 #include <cstdio> 3 #include <cstdlib> 4 #include <cstring> 5 #include <algorithm> 6 #include <stack> 7 #include <queue> 8 #include <cmath> 9 #include <map> 10 #define ll __int64 11 #define mod 1000000007 12 #define dazhi 2147483647 13 //#define N 530005 14 using namespace std; 15 ll n,l,r; 16 struct node 17 { 18 ll a,c,pos; 19 }N[100005]; 20 ll b[100005]; 21 bool cmp(struct node aa,struct node bb) 22 { 23 return aa.c<bb.c; 24 } 25 int main() 26 { 27 scanf("%I64d %I64d %I64d",&n,&l,&r); 28 for(ll i=1;i<=n;i++) 29 scanf("%I64d",&N[i].a); 30 for(ll i=1;i<=n;i++) 31 { 32 scanf("%I64d",&N[i].c); 33 N[i].pos=i; 34 } 35 sort(N+1,N+1+n,cmp); 36 b[N[1].pos]=l; 37 ll exm=l-N[1].a; 38 for(ll i=2;i<=n;i++) 39 { 40 ll st=l,en=r,mid; 41 while(st<en) 42 { 43 mid=(st+en)>>1; 44 if(mid-N[i].a>exm) 45 en=mid; 46 else 47 st=mid+1; 48 } 49 if(st-N[i].a>exm) 50 b[N[i].pos]=st; 51 else 52 { 53 printf("-1 "); 54 return 0; 55 } 56 exm=st-N[i].a; 57 } 58 for(ll i=1;i<=n;i++) 59 printf("%I64d ",b[i]); 60 return 0; 61 }
Dasha decided to have a rest after solving the problem. She had been ready to start her favourite activity — origami, but remembered the puzzle that she could not solve.
The tree is a non-oriented connected graph without cycles. In particular, there always are n - 1 edges in a tree with n vertices.
The puzzle is to position the vertices at the points of the Cartesian plane with integral coordinates, so that the segments between the vertices connected by edges are parallel to the coordinate axes. Also, the intersection of segments is allowed only at their ends. Distinct vertices should be placed at different points.
Help Dasha to find any suitable way to position the tree vertices on the plane.
It is guaranteed that if it is possible to position the tree vertices on the plane without violating the condition which is given above, then you can do it by using points with integral coordinates which don't exceed 1018 in absolute value.
The first line contains single integer n (1 ≤ n ≤ 30) — the number of vertices in the tree.
Each of next n - 1 lines contains two integers ui, vi (1 ≤ ui, vi ≤ n) that mean that the i-th edge of the tree connects vertices ui and vi.
It is guaranteed that the described graph is a tree.
If the puzzle doesn't have a solution then in the only line print "NO".
Otherwise, the first line should contain "YES". The next n lines should contain the pair of integers xi, yi (|xi|, |yi| ≤ 1018) — the coordinates of the point which corresponds to the i-th vertex of the tree.
If there are several solutions, print any of them.
7
1 2
1 3
2 4
2 5
3 6
3 7
YES
0 0
1 0
0 1
2 0
1 -1
-1 1
0 2
6
1 2
2 3
2 4
2 5
2 6
NO
4
1 2
2 3
3 4
YES
3 3
4 3
5 3
6 3
In the first sample one of the possible positions of tree is:
题意：给你一颗树 判断是否能够放在坐标轴中 要求每个点不能重合 每条边都平行于坐标轴
题解：dfs 前向星 存双向边 若某个点的度大于8则必然无法实现题目要求 从根结点开始向下遍历 每一层最多4个分支 每一层的边的长度随着深度的增加边的长度减少
这就可以防止相邻分支的重点
1 #include <iostream> 2 #include <cstdio> 3 #include <cstdlib> 4 #include <cstring> 5 #include <algorithm> 6 #include <stack> 7 #include <queue> 8 #include <cmath> 9 #include <map> 10 #define ll __int64 11 #define mod 1000000007 12 #define dazhi 2147483647 13 ll M=100000000000000000; 14 using namespace std; 15 struct node 16 { 17 int pre; 18 int to; 19 }N[35]; 20 int pre[50]; 21 int du[50]; 22 int n; 23 int l,r; 24 int nedge=0; 25 int mp[50]; 26 ll xxx[50],yyy[50]; 27 void add(int p,int t) 28 { 29 du[p]++; 30 du[t]++; 31 nedge++; 32 N[nedge].to=t; 33 N[nedge].pre=pre[p]; 34 pre[p]=nedge; 35 } 36 void dfs(int root,ll xx,ll yy,int de,int from) 37 { 38 mp[root]=1; 39 xxx[root]=xx; 40 yyy[root]=yy; 41 int gg=1; 42 for(int i=pre[root];i;i=N[i].pre) 43 { 44 if(mp[N[i].to]) 45 continue; 46 if((gg+from)==0) 47 { 48 gg++; 49 } 50 if(gg==1){ 51 dfs(N[i].to,xx,yy-(M>>de),de+1,-3); 52 } 53 if(gg==2) 54 dfs(N[i].to,xx-(M>>de),yy,de+1,-4); 55 if(gg==3) 56 dfs(N[i].to,xx,yy+(M>>de),de+1,-1); 57 if(gg==4) 58 dfs(N[i].to,xx+(M>>de),yy,de+1,-2); 59 gg++; 60 } 61 return ; 62 } 63 int main() 64 { 65 memset(du,0,sizeof(du)); 66 memset(pre,0,sizeof(pre)); 67 memset(mp,0,sizeof(mp)); 68 scanf("%d",&n); 69 for(int i=1;i<=n-1;i++) 70 { 71 scanf("%d %d",&l,&r); 72 add(l,r); 73 add(r,l); 74 } 75 for(int i=1;i<=n;i++) 76 { 77 if(du[i]>8){ 78 printf("NO "); 79 return 0; 80 } 81 } 82 printf("YES "); 83 ll x=0,y=0,deep=1; 84 dfs(1,x,y,deep,0); 85 for(int i=1;i<=n;i++) 86 printf("%I64d %I64d ",xxx[i],yyy[i]); 87 return 0; 88 }