Kris works in a large company "Blake Technologies". As a best engineer of the company he was assigned a task to develop a printer that will be able to print horizontal and vertical strips. First prototype is already built and Kris wants to tests it. He wants you to implement the program that checks the result of the printing.
Printer works with a rectangular sheet of paper of size n × m. Consider the list as a table consisting of n rows and m columns. Rows are numbered from top to bottom with integers from 1 to n, while columns are numbered from left to right with integers from 1 to m. Initially, all cells are painted in color 0.
Your program has to support two operations:
- Paint all cells in row ri in color ai;
- Paint all cells in column ci in color ai.
If during some operation i there is a cell that have already been painted, the color of this cell also changes to ai.
Your program has to print the resulting table after k operation.
The first line of the input contains three integers n, m and k (1 ≤ n, m ≤ 5000, n·m ≤ 100 000, 1 ≤ k ≤ 100 000) — the dimensions of the sheet and the number of operations, respectively.
Each of the next k lines contains the description of exactly one query:
- 1 ri ai (1 ≤ ri ≤ n, 1 ≤ ai ≤ 109), means that row ri is painted in color ai;
- 2 ci ai (1 ≤ ci ≤ m, 1 ≤ ai ≤ 109), means that column ci is painted in color ai.
Print n lines containing m integers each — the resulting table after all operations are applied.
3 3 3
1 1 3
2 2 1
1 2 2
3 1 3
2 2 2
0 1 0
5 3 5
1 1 1
1 3 1
1 5 1
2 1 1
2 3 1
1 1 1
1 0 1
1 1 1
1 0 1
1 1 1
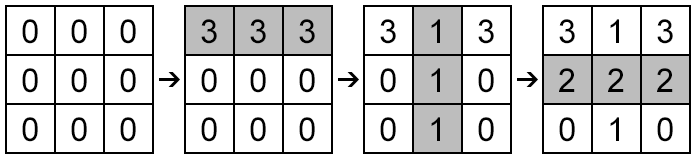
The figure below shows all three operations for the first sample step by step. The cells that were painted on the corresponding step are marked gray
题意: n*m的矩阵 两种操作 整行变换 与整列变换
1 ri ai (1 ≤ ri ≤ n, 1 ≤ ai ≤ 109), means that row ri is painted in color ai; 整行变为a
2 ci ai (1 ≤ ci ≤ m, 1 ≤ ai ≤ 109), means that column ci is painted in color ai. 整列变为a
输出k次变换后的矩阵;
题解:判断每一个位置上的数 其所在行的变换与所在列的变换的先后顺序以及变换结果 变换在后的 为结果 无变化的输出0;

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 using namespace std; 5 struct node 6 { 7 int sor; 8 int reu; 9 } a[5005],b[5005]; 10 int n,m,k; 11 int q,w,e; 12 int main() 13 { 14 scanf("%d %d %d",&n,&m,&k); 15 memset(a,0,sizeof(a)); 16 memset(b,0,sizeof(b)); 17 for(int i=1; i<=k; i++) 18 { 19 scanf("%d %d %d",&q,&w,&e); 20 if(q==1) 21 { 22 a[w].sor=i; 23 a[w].reu=e; 24 } 25 else 26 { 27 b[w].sor=i; 28 b[w].reu=e; 29 } 30 } 31 for(int i=1; i<=n; i++) 32 { 33 // cout<<a[i].sor<<" "<<b[i].sor<<endl; 34 if(a[i].sor>b[1].sor) 35 printf("%d",a[i].reu); 36 else 37 { 38 if(a[i].sor<b[1].sor) 39 printf("%d",b[1].reu); 40 else 41 printf("0"); 42 } 43 44 for(int j=2; j<=m; j++) 45 { 46 if(a[i].sor>b[j].sor) 47 printf(" %d",a[i].reu); 48 else 49 { 50 if(a[i].sor<b[j].sor) 51 printf(" %d",b[j].reu); 52 else 53 printf(" 0"); 54 } 55 } 56 printf(" "); 57 } 58 return 0; 59 }
