Codeforces Round #345 (Div. 2) C （multiset+pair ）

C. Watchmen

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Watchmen are in a danger and Doctor Manhattan together with his friend Daniel Dreiberg should warn them as soon as possible. There are n watchmen on a plane, the i-th watchman is located at point (xi, yi).

They need to arrange a plan, but there are some difficulties on their way. As you know, Doctor Manhattan considers the distance between watchmen i and j to be |xi - xj| + |yi - yj|. Daniel, as an ordinary person, calculates the distance using the formula .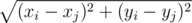

The success of the operation relies on the number of pairs (i, j) (1 ≤ i < j ≤ n), such that the distance between watchman i and watchmen j calculated by Doctor Manhattan is equal to the distance between them calculated by Daniel. You were asked to compute the number of such pairs.

Input

The first line of the input contains the single integer n (1 ≤ n ≤ 200 000) — the number of watchmen.

Each of the following n lines contains two integers xi and yi (|xi|, |yi| ≤ 109).

Some positions may coincide.

Output

Print the number of pairs of watchmen such that the distance between them calculated by Doctor Manhattan is equal to the distance calculated by Daniel.

Examples

input

3
1 1
7 5
1 5

output

2

input

6
0 0
0 1
0 2
-1 1
0 1
1 1

output

11

Note

In the first sample, the distance between watchman 1 and watchman 2 is equal to |1 - 7| + |1 - 5| = 10 for Doctor Manhattan and 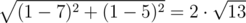 for Daniel. For pairs (1, 1), (1, 5) and (7, 5), (1, 5) Doctor Manhattan and Daniel will calculate the same distances.

题意： n个点  分别给出x，y坐标 

两种两点的计算方式  |xi - xj| + |yi - yj|.       .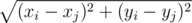

问 有多少种点的组合使得 两种两点的计算方式的结果相等      欧几里得距离等于曼哈顿距离

题解： 等式两边平方 整理移项之后可以发现  两点的x坐标相等或者y坐标相等情况下两种计算方式结果相等

用了 multiset+pair  

其中最关键的处理是 当x y都对应相等情况下 去重处理

用的是pair

x相等的+y相等的-xy相等的

#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#define ll __int64
using namespace std;
int n;
multiset<int>s1;
multiset<int>s2;
pair<int,int>gg;
multiset<pair<int,int > >ggg;
int a[200005],b[200005];
ll jishu=0;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        {
            scanf("%d %d",&a[i],&b[i]);
            gg.first=a[i];
            gg.second=b[i];
            ggg.insert(gg);
            s1.insert(a[i]);
            s2.insert(b[i]);
        }
    for(int i=1;i<=n;i++)
    {
       ll exm=s1.count (a[i]);
       jishu=jishu+exm*(exm-1)/2;
       s1.erase(a[i]);
    }
     for(int i=1;i<=n;i++)
    {
        ll exm=s2.count(b[i]);
       jishu=jishu+exm*(exm-1)/2;
        s2.erase(b[i]);
    }
    //printf("%I64d
",jishu);
    for(int i=1;i<=n;i++)
    {
        gg.first=a[i];
        gg.second=b[i];
        ll exm=ggg.count(gg);
            jishu=jishu-exm*(exm-1)/2;
        ggg.erase(gg);
    }
    printf("%I64d
",jishu);
    return 0;
}