B

Captain Flint and his crew keep heading to a savage shore of Byteland for several months already, drinking rum and telling stories. In such moments uncle Bogdan often remembers his nephew Denis. Today, he has told a story about how Denis helped him to come up with an interesting problem and asked the crew to solve it.

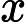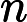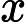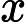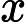
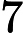
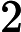
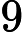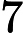
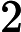
In the beginning, uncle Bogdan wrote on a board a positive integer x consisting of n digits. After that, he wiped out x and wrote integer k instead, which was the concatenation of binary representations of digits x consists of (without leading zeroes). For example, let x=729, then k=111101001 (since 7=111, 2=10, 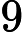9=1001).

After some time, uncle Bogdan understood that he doesn't know what to do with k and asked Denis to help. Denis decided to wipe last 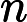n digits of k and named the new number as 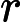r.

As a result, Denis proposed to find such integer 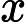x of length 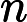n that 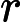r (as number) is maximum possible. If there are multiple valid 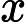x then Denis is interested in the minimum one.

All crew members, including captain Flint himself, easily solved the task. All, except cabin boy Kostya, who was too drunk to think straight. But what about you?

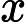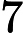
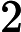
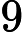
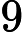
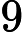
Note: in this task, we compare integers (x or k) as numbers (despite what representations they are written in), so 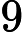729<1999 or 111<1000.

Input

The first line contains a single integer 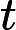t (1≤t≤1000) — the number of test cases.

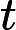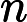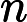
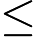
Next t lines contain test cases — one per test case. The one and only line of each test case contains the single integer n (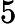1≤n≤105) — the length of the integer 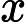x you need to find.

It's guaranteed that the sum of 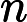n from all test cases doesn't exceed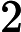 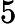2⋅105.

Output

For each test case, print the minimum integer 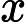x of length 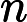n such that obtained by Denis number 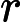r is maximum possible.

Example

input

Copy

2
1
3

output

Copy

8
998

Note

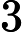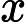
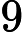
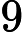
In the second test case (with n=3), if uncle Bogdan had x=998 then k=100110011000. Denis (by wiping last 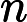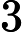n=3 digits) will obtain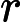 r=100110011.

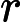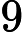
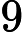
It can be proved that the 100110011 is the maximum possible r Denis can obtain and 998 is the minimum 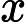x to obtain it.

题意

给定整数n，找出一个十进制数字x满足：长度为n，得到x在二进制下的串，去掉后面的n位，新二进制串是最大的，且数字x越小越好。

分析

我们将[0,9]数字分别转化为二进制串，可以观察到数字8,9的二进制串长度最长，分别为1000,1001由题干要求，抹除n位后的二进制串最大，那么利用贪心思想，要找到这样的串，那么十进制数字x的二进制串越长越好，于是我们可以断定这个x肯定由8or9组成。

但别忘了题干还要求我们数字x越小越好，为什么可以有这样的条件？拿数字8,9的二进制串1000,1001而言，当我们抹除最后1位时，得到的两个新串是相等的！于是但凡得到数字999...999，我们可以在合法的长度内将末位的几个99替换为88，

这样既保证二进制串大且原十进制数小的情况了，即x的组成肯定为999...888。

如何确定这一合法的替换长度呢？考虑到8/9二进制串长度为4。对于原数字x最末尾的(向上取整)n/4个要被去除的串，选8还是9的二进制串是没有区别的

#include <cstdio>
using namespace std;
int main(){
    int t;
    scanf("%d", &t);
    while(t--){
        int n;
        scanf("%d", &n);
        int l = n / 4; 
        if(n % 4 != 0) l++; 
        for (int i = 1; i <= n - l; i++) printf("9");
        for (int i = 1; i <= l; i++)     printf("8");
        printf("
");
    }
    return 0;
}