1、概述:也称为K最近邻算法,原理为搜索最近的k个已知类别样本,用于未知类别样本的预测。
对于分布不均匀的几个样本结果可能会受k取值的影响,通常情况下k值一般取奇数,此方法及可以用于连续型变量预测也可以作用于离散型数据模型预测。
2、衡量相似性指标方式:欧式距离、曼哈顿距离、cos余弦值、杰卡德相似系数等等
3、过程:
- 确定k
- 确定样本间相似度的度量指标,形成簇
- 根据各簇下类别最多的分类作为样本预测点
4、避免k值设定出现过拟合(K值过小)和欠拟合(K值选择过大)现象
对于K值设定过大的情况,可以更改设定权重为距离的倒数。另外一种常用的方式为多重交叉验证,k取不同的值,在每个k值下执行m重交叉验证,最后选定平均误差最小的k值。
5、余弦相似度
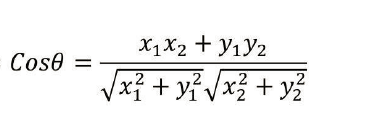

杰卡德相似系数(常用于用户推荐算法)值越大相似性越大
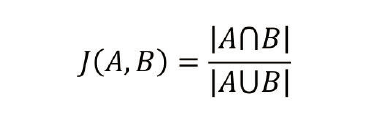
以上距离法构建样本时,一是需注意变量的数值化,若某个变量为离散型字符串,需要数值化处理(0,1,2...)。二是防止受数值变量的量纲影响,量纲可能影响距离,必要时需要进行转化,缩小归一化处理。
6、模型运行搜索方法
模型建立好以后常见的几种搜寻方法
- 暴力搜寻法(未知样本和已知样本的全表扫描)适合小样本数据,for循环迭代2次
- KD树搜寻法
- 球树搜寻法
暴力法搜索对于大样本数据集存在内存消耗大,运行速度慢等问题。
案例1(暴力搜寻法):
iris数据集模型,案例设定将样本分为2/3的训练解,和1/3的测试集,将测试集置于训练集中训练,比较返回样本点结果的准确率。测试集的每组数据在训练集中循环时,取K=3,每次取距离最近的3个值,循环完测试集数据,结果准确
率反映了此模型的效果。可以看到训练集模型预测结果准确率基本达到90%以上。此方法需建立2个for循环迭代训练集和测试集,固属于暴力搜寻法。
import csv
import random
import math
import operator
def loadDataset(filename, split, trainingSet = [], testSet = []):
with open(filename, 'rt') as csvfile:
lines = csv.reader(csvfile)
dataset = list(lines)
print(len(dataset))
for x in range(len(dataset)-1): #0-149
for y in range(4): #0-3
dataset[x][y] = float(dataset[x][y])
if random.random() < split:
trainingSet.append(dataset[x])
else:
testSet.append(dataset[x])
def euclideanDistance(instance1, instance2, length):
distance = 0
for x in range(length):
distance += pow((instance1[x]-instance2[x]), 2)
return math.sqrt(distance)
def getNeighbors(trainingSet, testInstance, k):
distances = []
length = len(testInstance)-1
for x in range(len(trainingSet)):
#testinstance
dist = euclideanDistance(testInstance, trainingSet[x], length)
distances.append((trainingSet[x], dist))
#distances.append(dist)
distances.sort(key=operator.itemgetter(1)) # 取元祖第一个域进行排序
neighbors = []
for x in range(k): #取distances数组前三项距离最小元祖里面的数组
neighbors.append(distances[x][0])
return neighbors
def getResponse(neighbors):
classVotes = {}
for x in range(len(neighbors)):
response = neighbors[x][-1]
if response in classVotes:
classVotes[response] += 1
else:
classVotes[response] = 1
sortedVotes = sorted(classVotes.items(), key=operator.itemgetter(1), reverse=True)
return sortedVotes[0][0]
def getAccuracy(testSet, predictions):
correct = 0
for x in range(len(testSet)):
if testSet[x][-1] == predictions[x]:
correct += 1
return (correct/float(len(testSet)))*100.0
def main():
#prepare data
trainingSet = []
testSet = []
split = 0.67
loadDataset(r'irisdata.txt', split, trainingSet, testSet)
print ('Train set: ' + repr(len(trainingSet)))
print ('Test set: ' + repr(len(testSet)))
#generate predictions
predictions = []
k = 3
for x in range(len(testSet)): # 0 - 测试集长度
# trainingsettrainingSet[x]
neighbors = getNeighbors(trainingSet, testSet[x], k)
result = getResponse(neighbors)
predictions.append(result)
print ('>predicted=' + repr(result) + ', actual=' + repr(testSet[x][-1]))
print ('predictions: ' + repr(predictions))
accuracy = getAccuracy(testSet, predictions)
print('Accuracy: ' + repr(accuracy) + '%')
if __name__ == '__main__':
main()
7、KD搜寻法
关键点:
1)根节点如何选择 计算训练集每个变量的方差,取最大方差的变量为根节点,按x[len(x)//2]分组成左右子节点
2)分割点如何选择 根据以上左右子节点分别按各自最大方差选出子节点中分割点,方法类似上面根节点的选择,比较x或y小于分割点的排到左边节点,否则到右边节点。
3)树停止生长的条件 kd树搜寻方法
例如11个样本点(1,1)、(1,5)、(2,3)、(4,7)、(5,2)、(6,4)、(7,1)、(8,8)、(9,2)、(9,5)、(10,3)。x方差9.87,y方差4.93,根节点为x,取x[len(11//2)]=x[5],(6,4)

具体搜寻原理为,预测数据进来先判断其在节点分割的哪个区域,与根节点比较,区域选定后判断其与区域中各个点的距离,选择距离最小值画圆。若满足圆与判定条件,x或y所在分割线没有交点,则停止搜寻。若有交点则选取其另外一侧节点区域,和其上级节点一起再次计算到各个点的距离,取距离最小值画圆,直到所画圆与节点分割线没有交点。则停止搜寻。
此方法存在缺点为,当所绘圆与某个矩形分割区域存在交点时,可能存在没有意义的搜寻。所以延伸出最佳方法球树搜寻法。
8、球树搜寻法
关键点:球心寻找和半径计算
原理:
1)首先构造超球体,球心为球内所以训练样本点最远的两两距离的中点。半径为该线段的一半。
2)超球体内离球心最远点p1,接着寻找离p1最远点p2,以此2个点为簇心,通过距离计算划分分2个数据块。
3)通过重复1)2)将这2个数据块划分为最小球体,直到不能分割为止。
搜寻过程:
通过搜寻离未知样本点最近的距离d,以及通过回流到最近叶节点球心的距离D,及第一个叶节点球体半径r,通过比较d+r与D的关系,若d+r<D则说明已是最短距离不需要回流了,反之还需要回流到上级区域,即D所在叶节点区域球体内寻找更近的样本点。重复直至搜索至根节点。
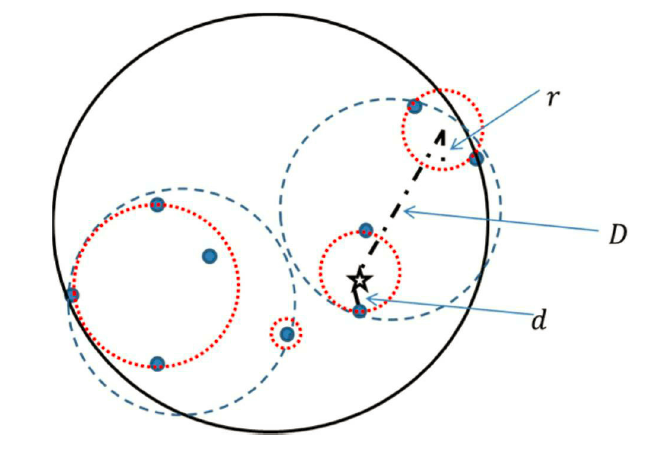
案列:
sklearn模块中,类KNeighborsClassfier可以用于分类,KNeighborsRegressor类可用于预测。
相关参数n_neighbors可用于指定临近样本k的个数,weights可指定投票权重,等等
煤气发电数据集案例:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import neighbors
from sklearn import model_selection
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
cp = pd.read_excel(r'CCPP.xlsx')
cp.head()
# AT 高炉温度 ,V 炉内压力 ,AP 炉内相对湿度 , RH 炉排气量 , PE 高炉发电量(连续型因变量)
# 1、自变量标准化处理量纲
from sklearn.preprocessing import minmax_scale
predictors = cp.columns[:-1]
X = minmax_scale(cp[predictors])
X_train, X_test, y_train, y_test = model_selection.train_test_split(X,
cp.PE,
test_size = 0.25,
random_state = 1234
)
# 2、使用均方误差MSE确认最近邻个数k
k = np.arange(1, np.ceil(np.log2(cp.shape[0])))
mse = []
for i in k :
cv_result = model_selection.cross_val_score(neighbors.KNeighborsRegressor(
n_neighbors = int(i),
weights = 'distance'),
X_train ,
y_train,
cv = 10,
scoring = 'neg_mean_squared_error'
)
mse.append((-1*cv_result).mean())
# 选择mse最小值
arg_min = np.array(mse).argmin()
plt.plot(k,mse)
plt.scatter(k,mse)
plt.text(k[arg_min], mse[arg_min]+0.5 , '最佳k值为%s' %int(k[arg_min] ))
plt.show()
绘制折线图如下:

得到最佳k值7。
# 3、对训练集建模
from sklearn import metrics
knn_reg = neighbors.KNeighborsRegressor(n_neighbors=7,
weights='distance'
)
knn_reg.fit(X_train,y_train)
predict = knn_reg.predict(X_test)
metrics.mean_squared_error(y_test,predict) # 计算MSE值,值越小,模型越好
结果输出为:

4、预测值与真实值的比较
pd.DataFrame({'Real':y_test,'Predict':predict},columns = ['Real','Predict']).head(10)

从结果可以看出knn模型预测值与实际值很接近,可以认为模型拟合的效果不错。
5、与决策树模型结果比较
from sklearn import tree
# 预设各参数的不同选项值
max_depth = [19,21,23,25,27]
min_samples_split = [2,4,6,8]
min_samples_leaf = [2,4,8,10,12]
parameters = {'max_depth':max_depth, 'min_samples_split':min_samples_split, 'min_samples_leaf':min_samples_leaf}
# 网格搜索法,测试不同的参数值
grid_dtreg = model_selection.GridSearchCV(estimator = tree.DecisionTreeRegressor(), param_grid = parameters, cv=10)
# 模型拟合
grid_dtreg.fit(X_train, y_train)
# 返回最佳组合的参数值
grid_dtreg.best_params_
# 构建用于回归的决策树
CART_Reg = tree.DecisionTreeRegressor(max_depth = 21, min_samples_leaf = 10, min_samples_split = 6)
# 回归树拟合
CART_Reg.fit(X_train, y_train)
# 模型在测试集上的预测
pred = CART_Reg.predict(X_test)
# 计算衡量模型好坏的MSE值
metrics.mean_squared_error(y_test, pred)
决策树输出结果:

通过以上KNN与决策树MSE值得比较发,KNN MSE值更小,固KNN模型更优。