08 决策树与随机森林
决策树之信息论基础
认识决策树
-
来源: 决策树的思想来源非常朴素,程序设计中的条件分支结构就是if - then 结构,最早的决策树就是利用这类结构分割数据的一种分类学习方法。
-
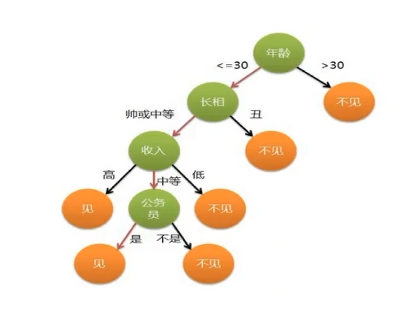
举例:是否见相亲对象
信息的度量和作用
-
克劳德 .艾尔伍德 .香农:信息论创始人,密西根大学学士,麻省理工学院博士。 1948年发表了划时代论文 - 通信的数学原理,奠定了现代信息论的基础。
-
信息的单位: 比特 (bit)

-
举例: 以32支球队争夺世界杯冠军
-
如果不知道任何球队的信息,每支球队得冠概率相等。
以二分法预测,最少需要使用5次才能预测到准确结果。 5 = log32 (以2为底)
5 = -(1/32log1/32 + 1/32log1/32 + ......) -
开放一些信息,则小于5bit, 如1/6 德国,1/6 巴西, 1/10 中国
5 > -(1/6log1/4 + 1/6log1/4 + ....)
- 信息熵:
- “谁是世界杯冠军”的信息量应该比5 bit少, 它的准确信息量应该是:
- H = -(p1logp1 + p2logp2 + p3logp3 +......p32logp32 ) Pi 为第i支球队获胜的概率
- H 的专业术语就是信息熵,单位为比特
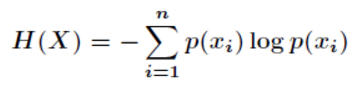
决策树的划分以及案例
信息增益
-
定义: 特征A对训练数据集D的信息增益g(D,A), 定义为集合D的信息熵H(D)与特征A给定条件下D的信息条件熵H(D|A) 之差,即:
g(D,A) = H(D) - H(D | A)
注: 信息增益表示得知特征 X 的信息而使得类 Y的信息的不确定性减少的程度。

-
以不同特征下的信贷成功率为例
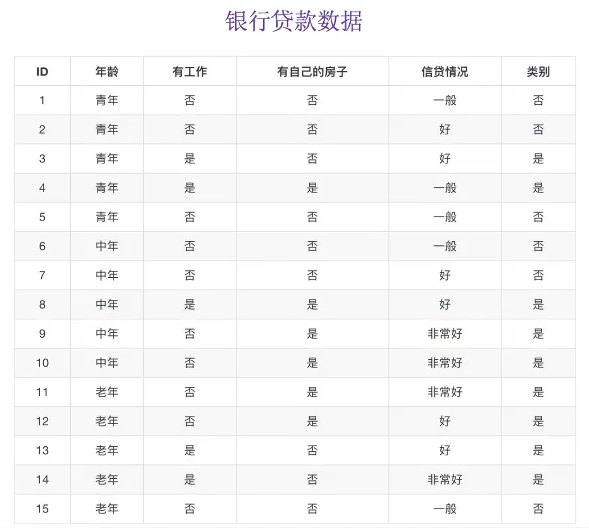
- H(D) = -(9/15log(9/15) + 6/15log(6/15)) = 0.971 # 以类别进行判断,只有是否两种类别
- gD,年纪) = H(D) - H(D'|年纪) = 0.971 - [1/3H(青年)+ 1/3H(中年)+ 1/3H(老年)] # 三种年纪对应的目标值均占1/3
- H(青年) = -(2/5log(2/5) + 3/5log(3/5)) # 青年类型中,类别的目标值特征为(2/5, 3/5)
- H(中年) = -(2/5log(2/5) + 3/5log(3/5))
- H(老年) = -(4/5log(2/5) + 1/5log(3/5))
令A1, A2, A3, A4 分别表示年龄,有工作,有房子和信贷情况4个特征,则对应的信息增益为:
g(D,A1) = H(D) - H(D|A1)
其中,g(D,A2) = 0.324 , g(D,A3) = 0.420 , g(D,A4) = 0.363
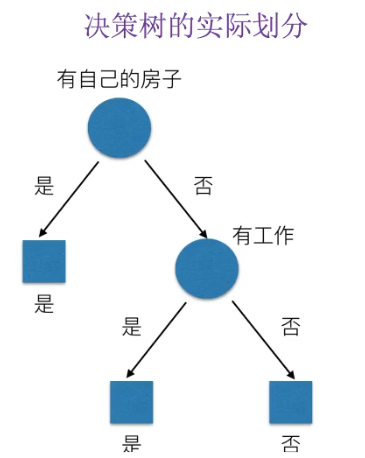
相比而言,A3特征(有房子)的信息增益最大,为最有用特征。
所以决策树的实际划分为:
常见决策树使用的算法
- ID3
- 信息增益,最大原则
- C4.5
- 信息增益比最大原则 (信息增益占原始信息量的比值)
- CART
- 回归树: 平方误差最小
- 分类树: 基尼系数最小原则 (划分的细致),sklearn默认的划分原则
Sklearn决策树API
- sklearn.tree.DecisionTreeClassifier(criterion='gini', max_depth=None, random_state=None)
- criterion (标准): 默认基尼系数,也可以选用信息增益的熵‘entropy’
- max_depth: 树的深度大小
- random_state: 随机数种子
- 决策树结构
sklearn.tree.export_graphviz() 导出DOT文件格式
- estimator: 估算器
- out_file = "tree.dot" 导出路径
- feature_name = [,] 决策树特征名
决策树预测泰坦尼克号案例
import pandas as pd
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, export_graphviz
"""
泰坦尼克数据描述事故后乘客的生存状态,该数据集包括了很多自建旅客名单,提取的数据集中的特征包括:
票的类别,存货,等级,年龄,登录,目的地,房间,票,船,性别。
乘坐等级(1,2,3)是社会经济阶层的代表,其中age数据存在缺失。
"""
def decision():
"""
决策树对泰坦尼克号进行预测生死
:return: None
"""
# 1.获取数据
titan = pd.read_csv('./titanic_train.csv')
# 2.处理数据,找出特征值和目标值
x = titan[['Pclass', 'Age', 'Sex']]
y = titan[['Survived']]
# print(x)
# 缺失值处理 (使用平均值填充)
x['Age'].fillna(x['Age'].mean(), inplace=True)
print(x)
# 3.分割数据集到训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)
# 4. 进行处理(特征工程) 特征,类别 --> one_hot编码
dict = DictVectorizer(sparse=False)
x_train = dict.fit_transform(x_train.to_dict(orient='records'))
print(dict.get_feature_names())
x_test = dict.transform(x_test.to_dict(orient='records')) # 默认一行一行转换成字典
print(x_train)
# 5. 用决策树进行预测
dec = DecisionTreeClassifier()
dec.fit(x_train, y_train)
# 预测准确率
print("预测的准确率:", dec.score(x_test, y_test))
# 导出决策树
export_graphviz(dec, out_file='./tree.dot', feature_names=['Pclass', 'Age', 'Sex'])
return None
if __name__ == '__main__':
decision()
随机森林
集成学习方法
- 定义:集成学习通过建立几个模型组合,来解决单一预测问题。其工作原理是生成多个分类器 / 模型,各组独立地学习和作出预测。这些预测最后结合成单预测,因此优于任何一个单分类的租出预测。
随机森林
-
定义:在机器学习中,随机森林是一个包含多个决策树的分类器,并且其输出的类别是由个别树输出的类别的众数而定。
例如: 训练了5棵树,其中4棵树的结果是True, 1棵树为False, 那么最终的结果就是True. (投票) -
问题: 如果每棵树使用相同的特征,相同的分类器,参数也相同,建立的每棵树不就是相同的么?
随机森林建立多个决策树的过程:
单个树的建立:(N个样本,M个特征)
- 随机在N个样本中选择一个样本,重复N次, 样本有可能重复
- 随机在M个特征当中选出m个特征 m << M
- 建立10棵决策树,样本,特征大多不一样 随机有放回的抽样 (bootstrap抽样)
为什么要随机抽样训练集?
如果不随机抽样,每棵树的训练集都一样,那么最终训练处的树分类结果也是完全一样的
为什么要有放回的抽样?
如果不是有放回的抽样,那么每棵树的训练样本都是不同的,都是没有交集的,这样的每棵树都是“有偏的”,“片面的”。即,每棵树训练出来都是有很大的差异,而随机森铃最后分类取决于多棵树(弱分类器)的投票表决。
随机森林 API
- 分类器:sklearn.ensemble.RandomForestClassifier
- n_estimators:integer(整数),option, default=10 (森林里数目的数量)
- criteria: string (default ='gini') 分割特征的测量方法
- max_depth 树的最大深度
- max_feature = 'auto' 每个决策树的最大特征数量
- bootstrap: default = True 是否放回抽样
随机森林的优点
- 在当前的所有算法中,具有极好的准确率
- 能有有效地运行在大数据集上 (样本,特征)
- 能够处理具有高维特征的输入样本,不需要降维
- 能够评估各个特征在分类问题上的重要性
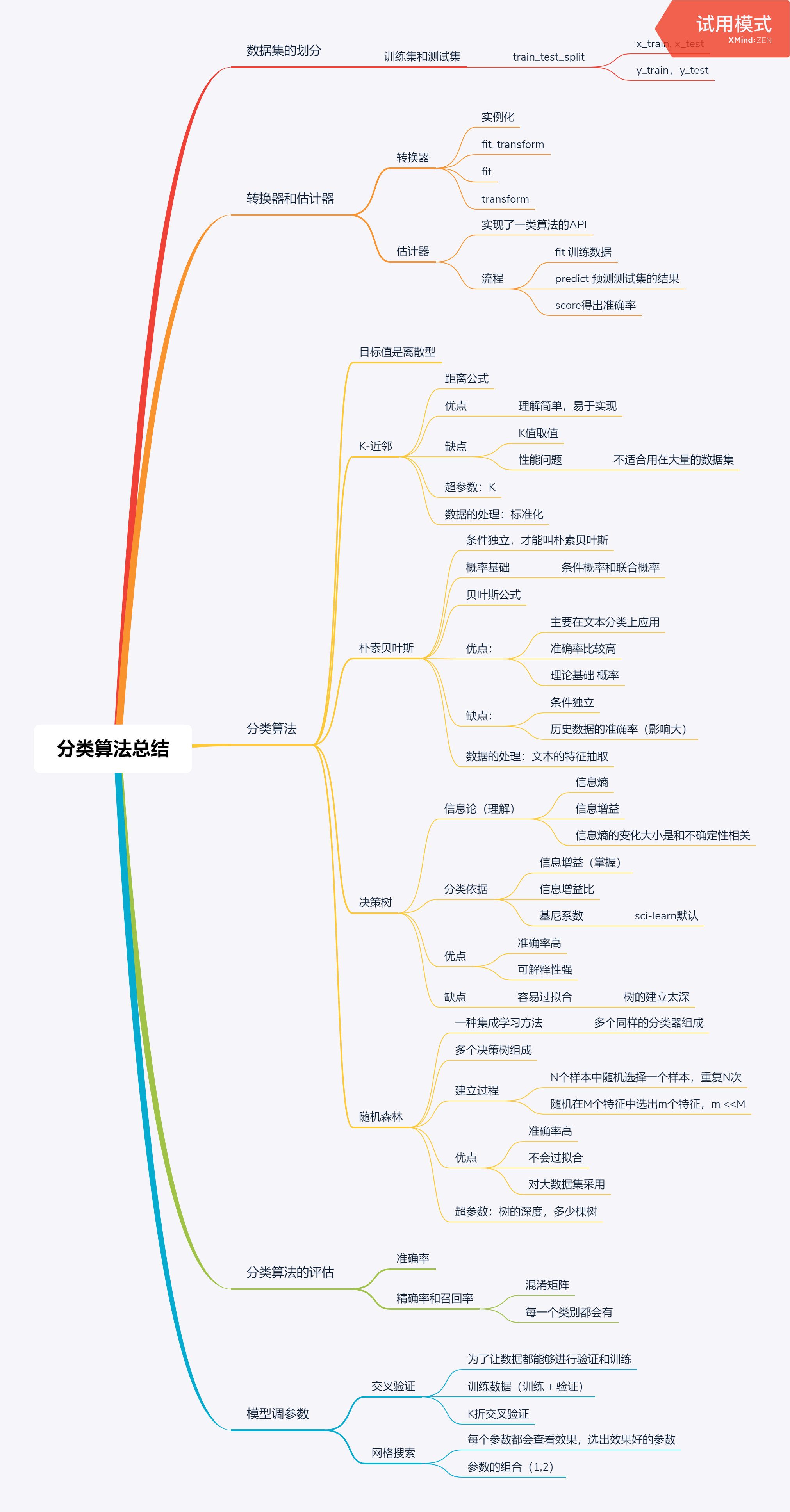
分类算法总结