1、蒙特卡洛方法
蒙特卡罗方法又称统计模拟法、随机抽样技术,是一种随机模拟方法,以概率和统计理论方法为基础的一种计算方法,是使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系,用电子计算机实现统计模拟或抽样,以获得问题的近似解。为象征性地表明这一方法的概率统计特征,数学家冯·诺依曼用闻名世界的赌城——蒙特卡罗命名(就是那个冯·诺依曼)。
蒙特卡罗方法解题过程的主要步骤:
a.针对实际问题建立一个简单且便于实现的概率统计模型,使所求的量恰好是该模型的概率分布或数字特征。
b.对模型的随机变量建立抽样方法,在计算机上进行模拟测试,抽取足够多的随机数。
c.对模拟实验结果进行统计分析,给出所求解的“估计”。
d.必要时,改进模型以提高估计精度和减少实验费用,提高模拟效率。
2、冯·诺依曼
冯·诺依曼(John von Neumann,1903~1957),20世纪最重要的数学家之一,在现代计算机、博弈论和核武器等诸多领域内有杰出建树的最伟大的科学全才之一,被称为“计算机之父”和“博弈论之父”。主要贡献是:2进制思想与程序内存思想,当然还有蒙特卡洛方法。通过第一部分,可知,蒙特卡洛方法更多的是一种思想的体现(这点远不同于快排等“严格”类算法),下面介绍最常见的一种应用——随机数生成。
3、U(0,1)随机数的产生
对随机系统进行模拟,便需要产生服从某种分布的一系列随机数。最常用、最基础的随机数是在(0,1)区间内均匀分布的随机数,最常用的两类数值计算方法是:乘同余法和混合同余法。
乘同余法: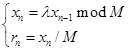 其中,
其中,![]() 被称为种子,
被称为种子,![]() 是模,
是模,![]() 是(0,1)区间的随机数。
是(0,1)区间的随机数。
混合同余法:![clip_image002[10] clip_image002[10]](https://images0.cnblogs.com/blog/532915/201406/232228021116613.png) 其中,
其中,![]() 是非负整数。
是非负整数。
这些随机数是具有周期性的,模拟参数的选择不同,产生的随机数质量也有所差异。更复杂的生成方法还有:
![clip_image002[14] clip_image002[14]](https://images0.cnblogs.com/blog/532915/201406/232228057833502.png)
4、从U(0,1)到其它概率分布的随机数
离散型随机数的模拟
设随机变量X的概率分布为:![]() ,分布函数有
,分布函数有![]()
设随机变量U~U(0,1)的均匀分布,则![]() ,表明
,表明![]() 的概率与随机变量u落在
的概率与随机变量u落在![]() 与
与![]() 之间的概率相同。
之间的概率相同。
例如:离散随机变量X有分布律
| X | 0 | 1 | 2 |
| P(x) | 0.3 | 0.3 | 0.4 |
U是(0,1)的均匀分布,则有![clip_image002[28] clip_image002[28]](https://images0.cnblogs.com/blog/532915/201406/232228077369832.png) ,这样得到的x便具有X的分布律。
,这样得到的x便具有X的分布律。
连续型随机变量的模拟
常用的有两种方法:逆变换法和舍选法。逆变换法
定理:设随机变量Y的分布函数为F(y)是连续函数,而U是(0,1)上均匀分布的随机变量。另![]() ,则X和Y具有相同的分布。
,则X和Y具有相同的分布。
证明:由定义知,X的分布函数![]()
所以X和Y具有相同的分布。
这样计算得![]() ,带入均匀分布的U,即可得到服从
,带入均匀分布的U,即可得到服从![]() 的随机数Y。
的随机数Y。
例如:设X~U(a,b),则其分布函数为
![clip_image002[42] clip_image002[42]](https://images0.cnblogs.com/blog/532915/201406/232228092525563.png) 则
则![]() 。所以生成U(0,1)的随机数U,则
。所以生成U(0,1)的随机数U,则![]() 便是来自U(a,b)的随机数。
便是来自U(a,b)的随机数。
有些随机变量的累计分布函数不存在或者难以求出,即使存在,但计算困难,于是提出了舍选法
要产生服从![]() 的随机数,设x的值域为[a,b],抽样过程如下:
的随机数,设x的值域为[a,b],抽样过程如下:
1.已知随机分布![]() 且x的取值区间也为[a,b],并要求
且x的取值区间也为[a,b],并要求![]() ,如图:
,如图: ![clip_image002[56] clip_image002[56]](https://images0.cnblogs.com/blog/532915/201406/242159224396964.png)
2.从![]() 中随机抽样得
中随机抽样得![]() ,然后由
,然后由![]() 的均匀分布抽样得
的均匀分布抽样得![]() 。
。
3.接受或舍弃取样值![]() ,如果
,如果![]() 舍弃该值;返回上一步,否则接受。几何解释如下:
舍弃该值;返回上一步,否则接受。几何解释如下: 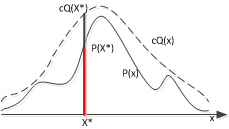
常数c的选取:c应该尽可能地小,因为抽样效率与c成反比;一般取![]() 。这里的
。这里的![]() 可以取均匀分布,这样由第二步中两个均匀分布便能得到其他任意分布的模拟抽样。
可以取均匀分布,这样由第二步中两个均匀分布便能得到其他任意分布的模拟抽样。
5、正态随机数的生成
除了上面的反函数法和舍选法,正态随机数还可以根据中心极限定理和Box Muller(坐标变换法)得到。
中心极限定理:如果随机变量序列 ![]() 独立同分布,并且具有有限的数学期望和方差
独立同分布,并且具有有限的数学期望和方差![]() ,则对于一切
,则对于一切![]() 有
有
![clip_image002[80] clip_image002[80]](https://images0.cnblogs.com/blog/532915/201406/242223491273213.png)
也就是说,当n个独立同分布的变量和,服从![]() 的正态分布(n足够大时)。
的正态分布(n足够大时)。
设n个独立同分布的随机变量![]() ,它们服从U(0,1)的均匀分布,那么
,它们服从U(0,1)的均匀分布,那么![]() 渐近服从正态分布
渐近服从正态分布![]() 。
。
Box Muller方法,设(X,Y)是一对相互独立的服从正态分布![]() 的随机变量,则有概率密度函数:
的随机变量,则有概率密度函数: ![]()
令![]() ,其中
,其中![]() ,则
,则![]() 有分布函数:
有分布函数: ![]()
令![]() ,则分布函数的反函数得:
,则分布函数的反函数得:![]() 。
。
如果![]() 服从均匀分布U(0,1),则
服从均匀分布U(0,1),则![]() 可由
可由![]() 模拟生成(
模拟生成(![]() 也为均匀分布,可被
也为均匀分布,可被![]() 代替)。令
代替)。令![]() 为
为![]() ,
,![]() 服从均匀分布U(0,1)。得:
服从均匀分布U(0,1)。得: ![]()
X和Y均服从正态分布。用Box Muller方法来生成服从正态分布的随机数是十分快捷方便的。